
1、試題特點
(1) 高考集合與簡易邏輯試題考查情況
2008年的高考在全國19套試卷中,都有體現,重點考查了集合間關系、集合的運算、充分條件與必要條件、四種命題等.
據此可知,有關集合與簡易邏輯的試題是高考命題的重要題型,它的解答需要用到集合與簡邏輯的基礎知識、基本性質,及一些相關知識,如不等式、指數函數、對數函數等,其命題熱點是伴隨相關知識的考查,出現頻率較高的題型是有關不等式的命題。
(2) 主要特點
縱觀近年來高考試題,特別是2008年高考試題,集合與簡易邏輯試題有如下特點:
(1)全方位. 近幾年來的高考題中,集合與簡易邏輯的所有知識點都考過,雖然近幾年不強調知識的覆蓋率,但每一年集合與簡易邏輯知識點的覆蓋率依然沒有減小.
(2)巧綜合. 為了突出集合與簡易邏輯在中學中的重要地位,近幾年來高考強化了集合、簡易邏輯與其它知識的聯系,如集合與不等式、對數函數、指函數等知識的綜合都有出現.
(3)變角度. 出于“立意”和創設情景的需要,集合與簡易邏輯試題設置問題的角度和方式也不斷創新,重視數學思想的考查,加大了應用題、探索題、開放題和信息題的考查力度,如2008廣東文的第1題,2008江西理科的第2題,從而使集合與簡易邏輯考題顯得新穎、生動、靈活.
7.已知定義在正實數集上的函數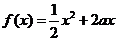 ,
,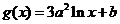 ,其中
,其中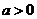 .設兩曲線
.設兩曲線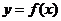 ,
,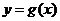 有公共點,且在該點處的切線相同.用
有公共點,且在該點處的切線相同.用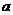 表示
表示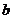 ,并求
,并求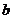 的最大值;
的最大值;
解析:設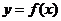 與
與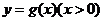 在公共點
在公共點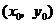 處的切線相同.
處的切線相同.
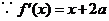 ,
,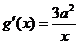 ,由題意
,由題意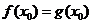 ,
,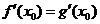 .
.
即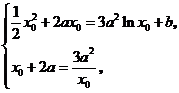 由
由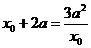 得:
得: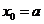 ,或
,或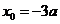 (舍去).
(舍去).
即有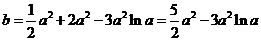 .
.
令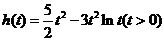 ,則
,則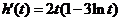 .于是當
.于是當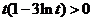 ,即
,即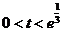 時,
時,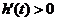 ;當
;當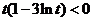 ,即
,即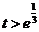 時,
時,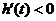 .故
.故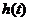 在
在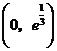 為增函數,
為增函數,
在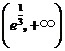 為減函數,∴
為減函數,∴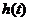 在
在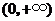 的最大值為
的最大值為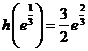 .
.

6. 設函數
設函數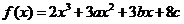 在
在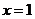 及
及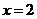 時取得極值.
時取得極值.
(Ⅰ)求a、b的值;(Ⅱ)若對于任意的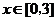 ,都有
,都有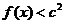 成立,求c的取值范圍.
成立,求c的取值范圍.
解析:(Ⅰ)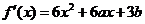 ,由
,由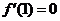 ,
,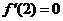 .解得
.解得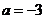 ,
,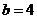 .
.
(Ⅱ)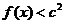 在[0,3]上恒成立即
在[0,3]上恒成立即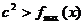 ,
,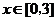
由(Ⅰ)可知,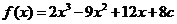 ,
,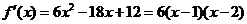 .
.
當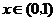 時,
時,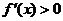 ;當
;當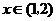 時,
時,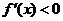 ;當
;當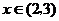 時,
時,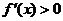 .
.
即 在
在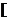 0,1]上遞增,[1,2]上遞減,[2,3]上遞增;∴當
0,1]上遞增,[1,2]上遞減,[2,3]上遞增;∴當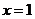 時,
時, 取得極大值
取得極大值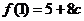 ,又
,又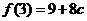 .故當
.故當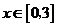 時,
時, 的最大值為
的最大值為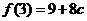 .
.
于是有: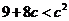 ,解得
,解得 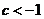 或
或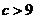 ,因此
,因此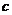 的取值范圍為
的取值范圍為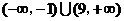 。
。
5.已知函數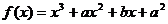 在
在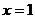 處有極值10,則
處有極值10,則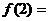
解析: 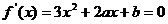 ,∴
,∴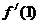 =
=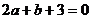 ①
①
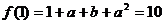 ②
由①②得:
②
由①②得: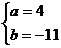 或
或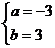
當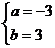 時,
時,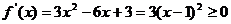 ,此時函數
,此時函數 無極值,舍去;
無極值,舍去;
當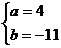 時
時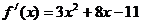 ,函數
,函數 在
在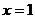 處左減右增,有極小值;
處左減右增,有極小值;
此時∴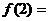 18 。
18 。
4.已知函數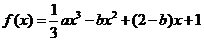 在
在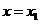 處取得極大值,在
處取得極大值,在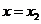 處取得極小值,且
處取得極小值,且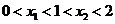 .(1)證明
.(1)證明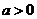 ;(2)若z=a+2b,求z的取值范圍。
;(2)若z=a+2b,求z的取值范圍。
解析:函數 的導數
的導數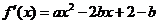 .
.
(Ⅰ)由函數 在
在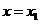 處取得極大值,在
處取得極大值,在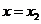 處取得極小值,知
處取得極小值,知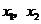 是
是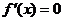 的兩個根.所以
的兩個根.所以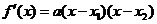 ;當
;當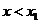 時,
時, 為增函數,
為增函數,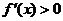 ,由
,由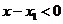 ,
,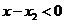 得
得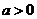 .
.
(Ⅱ)在題設下,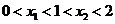 等價于
等價于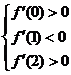 即
即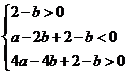 .
.
化簡得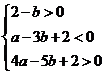 .此不等式組表示的區域為平面
.此不等式組表示的區域為平面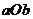 上三條直線:
上三條直線:
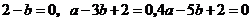 所圍成的
所圍成的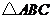 的內部,由“線性規劃”的知識容易求得:
的內部,由“線性規劃”的知識容易求得: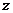 的取值范圍為
的取值范圍為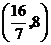 .
.
3.f(x)是定義在(0,+∞)上的非負可導函數,且滿足xf/(x)+f(x)≤0,對任意正數a、b,若a<b,則必有 ( ) (07陜西理11)
A.af(b) ≤bf(a) B.bf(a) ≤af(b)
C.af(a) ≤f(b) D.bf(b) ≤f(a)
解析:xf/(x)+f(x)≤0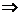 [xf(x)]/ ≤0
[xf(x)]/ ≤0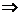 函數F(x)= xf(x) 在(0,+∞)上為常函數或遞減,
函數F(x)= xf(x) 在(0,+∞)上為常函數或遞減,
又0<a<b且f(x)非負,于是有:af(a)≥bf(b)≥0 ① 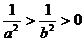 ②
②
①②兩式相乘得: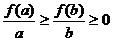
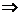 af(b) ≤bf(a),故選A。
af(b) ≤bf(a),故選A。
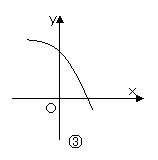
2.已知定義在R上的函數y=f(x)的導函數f/(x)在R上也可導,且其導函數[f/(x)]/<0,
則y=f(x)的圖象可能是下圖中的 ( )
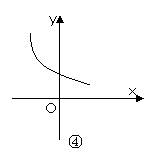
 A.①② B.①③ C.②③
D.③④
A.①② B.①③ C.②③
D.③④
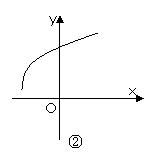
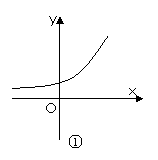
C解析:由[f/(x)]/<0知f/(x)在R上遞減,即函數y=f(x)的圖象上從左到右各點處的切線斜率遞減,不難看出圖象②③滿足這一要求。
1.已知函數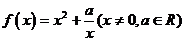 若
若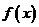 在
在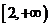 是增函數,求實數
是增函數,求實數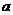 的范圍。
的范圍。
解析: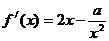 ≥0在
≥0在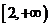 上恒成立
上恒成立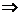
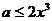 在
在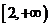 上恒成立
上恒成立
而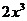 在
在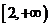 上的最小值為16,故
上的最小值為16,故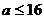 。
。
5.構造函數證明不等式.
典型例題
例7.(2006年天津卷)函數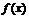 的定義域為開區間
的定義域為開區間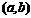 ,導函數
,導函數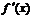 在
在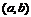 內的圖象如圖所示,則函數
內的圖象如圖所示,則函數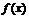 在開區間
在開區間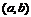 內有極小值點( )
內有極小值點( )
A.1個
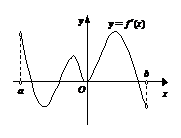 B.2個
B.2個
C.3個
D. 4個
[考查目的]本題主要考查函數的導數和函數圖象性質等基礎知識的應用能力.
[解答過程]由圖象可見,在區間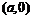 內的圖象上有一個極小值點.
內的圖象上有一個極小值點.
故選A.
例8 .(2007年全國一)設函數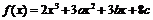 在
在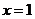 及
及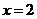 時取得極值.
時取得極值.
(Ⅰ)求a、b的值;
(Ⅱ)若對于任意的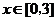 ,都有
,都有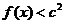 成立,求c的取值范圍.
成立,求c的取值范圍.
思路啟迪:利用函數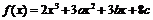 在
在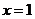 及
及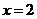 時取得極值構造方程組求a、b的值.
時取得極值構造方程組求a、b的值.
解答過程:(Ⅰ)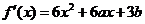 ,
,
因為函數 在
在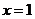 及
及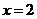 取得極值,則有
取得極值,則有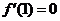 ,
,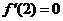 .
.
即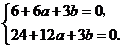
解得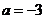 ,
,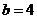 .
.
(Ⅱ)由(Ⅰ)可知,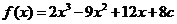 ,
,
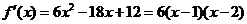 .
.
當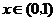 時,
時,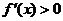 ;
;
當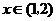 時,
時,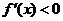 ;
;
當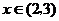 時,
時,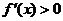 .
.
所以,當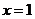 時,
時, 取得極大值
取得極大值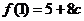 ,又
,又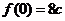 ,
,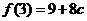 .
.
則當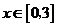 時,
時, 的最大值為
的最大值為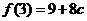 .
.
因為對于任意的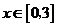 ,有
,有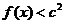 恒成立,
恒成立,
所以 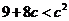 ,
,
解得 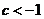 或
或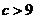 ,
,
因此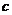 的取值范圍為
的取值范圍為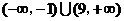 .
.
例9.函數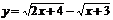 的值域是_____________.
的值域是_____________.
思路啟迪:求函數的值域,是中學數學中的難點,一般可以通過圖象觀察或利用不等式性質求解,也可以利用函數的單調性求出最大、最小值。此例的形式結構較為復雜,采用導數法求解較為容易。
解答過程:由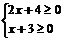 得,
得,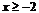 ,即函數的定義域為
,即函數的定義域為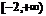 .
.
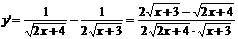 ,
,
又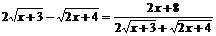 ,
,
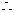 當
當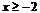 時,
時,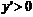 ,
,
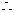 函數
函數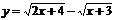 在
在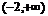 上是增函數,而
上是增函數,而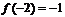 ,
,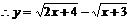 的值域是
的值域是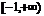 .
.
例10.(2006年天津卷)已知函數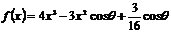 ,其中
,其中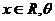 為參數,且
為參數,且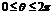 .
.
(1)當時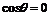 ,判斷函數
,判斷函數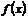 是否有極值;
是否有極值;
(2)要使函數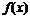 的極小值大于零,求參數
的極小值大于零,求參數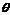 的取值范圍;
的取值范圍;
(3)若對(2)中所求的取值范圍內的任意參數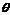 ,函數
,函數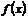 在區間
在區間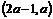 內都是增函數,求實數
內都是增函數,求實數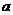 的取值范圍.
的取值范圍.
[考查目的]本小題主要考查運用導數研究三角函數和函數的單調性及極值、解不等式等基礎知識,考查綜合分析和解決問題的能力,以及分類討論的數學思想方法.
[解答過程](Ⅰ)當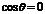 時,
時,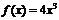 ,則
,則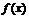 在
在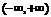 內是增函數,故無極值.
內是增函數,故無極值.
(Ⅱ)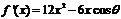 ,令
,令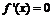 ,得
,得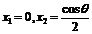 .
.
由(Ⅰ),只需分下面兩種情況討論.
①當
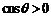 時,隨x的變化
時,隨x的變化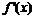 的符號及
的符號及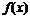 的變化情況如下表:
的變化情況如下表:
|
x |
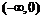 |
0 |
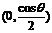 |
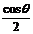 |
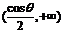 |
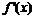 |
+ |
0 |
- |
0 |
+ |
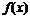 |
↗ |
極大值 |
↘ |
極小值 |
↗ |
因此,函數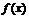 在
在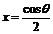 處取得極小值
處取得極小值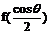 ,且
,且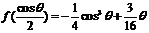 .
.
要使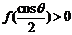 ,必有
,必有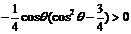 ,可得
,可得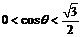 .
.
由于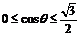 ,故
,故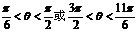 .
.
②當時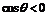 ,隨x的變化,
,隨x的變化,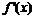 的符號及
的符號及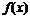 的變化情況如下表:
的變化情況如下表:
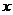 |
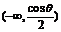 |
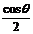 |
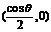 |
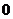 |
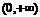 |
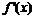 |
+ |
0 |
- |
0 |
+ |
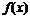 |
 |
極大值 |
 |
極小值 |
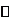 |
因此,函數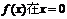 處取得極小值
處取得極小值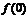 ,且
,且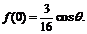
若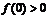 ,則
,則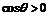 .矛盾.所以當
.矛盾.所以當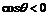 時,
時,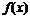 的極小值不會大于零.
的極小值不會大于零.
綜上,要使函數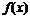 在
在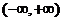 內的極小值大于零,參數
內的極小值大于零,參數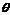 的取值范圍為
的取值范圍為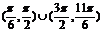 .
.
(III)解:由(II)知,函數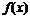 在區間
在區間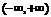 與
與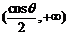 內都是增函數。
內都是增函數。
由題設,函數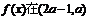 內是增函數,則a須滿足不等式組
內是增函數,則a須滿足不等式組
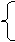
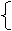
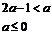 或
或 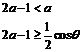
由(II),參數時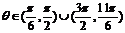 時,
時,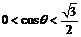 .要使不等式
.要使不等式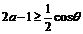 關于參數
關于參數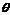 恒成立,必有
恒成立,必有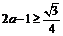 ,即
,即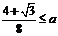 .
.
綜上,解得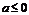 或
或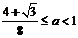 .
.
所以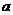 的取值范圍是
的取值范圍是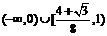 .
.
例11.(2006年山東卷)設函數f(x)=ax-(a+1)ln(x+1),其中a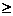 -1,求f(x)的單調區間.
-1,求f(x)的單調區間.
[考查目的]本題考查了函數的導數求法,函數的極值的判定,考查了應用數形結合的數學思想分析問題解決問題的能力
[解答過程]由已知得函數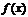 的定義域為
的定義域為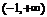 ,且
,且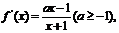
(1)當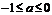 時,
時,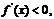 函數
函數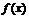 在
在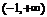 上單調遞減,
上單調遞減,
(2)當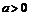 時,由
時,由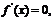 解得
解得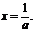
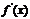 、
、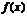 隨
隨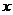 的變化情況如下表
的變化情況如下表
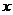 |
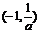 |
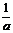 |
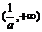 |
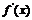 |
- |
0 |
+ |
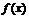 |
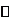 |
極小值 |
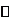 |
從上表可知
當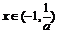 時,
時,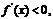 函數
函數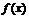 在
在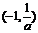 上單調遞減.
上單調遞減.
當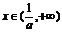 時,
時,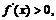 函數
函數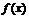 在
在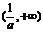 上單調遞增.
上單調遞增.
綜上所述:當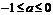 時,函數
時,函數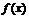 在
在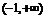 上單調遞減.
上單調遞減.
當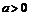 時,函數
時,函數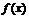 在
在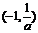 上單調遞減,函數
上單調遞減,函數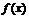 在
在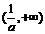 上單調遞增.
上單調遞增.
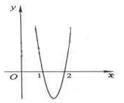 例12.(2006年北京卷)已知函數
例12.(2006年北京卷)已知函數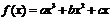 在點
在點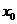 處取得極大值
處取得極大值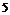 ,其導函數
,其導函數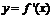 的圖象經過點
的圖象經過點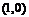 ,
,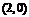 ,如圖所示.求:
,如圖所示.求:
(Ⅰ)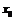 的值;
的值;
(Ⅱ)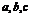 的值.
的值.
[考查目的]本小題考查了函數的導數,函數的極值的判定,閉區間上二次函數的最值, 函數與方程的轉化等基礎知識的綜合應用,考查了應用數形結合的數學思想分析問題解決問題的能力
[解答過程]解法一:(Ⅰ)由圖像可知,在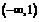 上
上
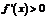 ,在
,在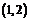 上
上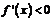 ,在
,在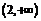 上
上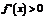 ,
,
故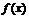 在
在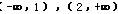 上遞增,在
上遞增,在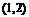 上遞減,
上遞減,
因此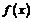 在
在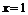 處取得極大值,所以
處取得極大值,所以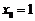
(Ⅱ)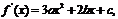
由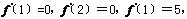
得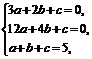
解得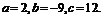
解法二:(Ⅰ)同解法一
(Ⅱ)設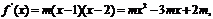
又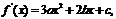
所以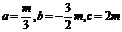
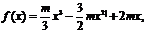
由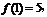 即
即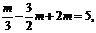 得
得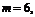
所以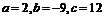
例13.(2006年湖北卷)設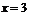 是函數
是函數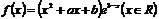 的一個極值點.
的一個極值點.
(Ⅰ)求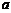 與
與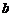 的關系式(用
的關系式(用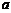 表示
表示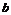 ),并求
),并求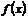 的單調區間;
的單調區間;
(Ⅱ)設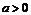 ,
,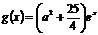 .若存在
.若存在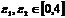 使得
使得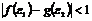 成立,求
成立,求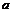 的取值范圍.
的取值范圍.
[考查目的]本小題主要考查函數、不等式和導數的應用等知識,考查綜合運用數學知識解決問題的能力.
[解答過程](Ⅰ)f `(x)=-[x2+(a-2)x+b-a ]e3-x,
由f `(3)=0,得 -[32+(a-2)3+b-a ]e3-3=0,即得b=-3-2a,
則 f `(x)=[x2+(a-2)x-3-2a-a ]e3-x
=-[x2+(a-2)x-3-3a ]e3-x=-(x-3)(x+a+1)e3-x.
令f `(x)=0,得x1=3或x2=-a-1,由于x=3是極值點,
所以x+a+1≠0,那么a≠-4.
當a<-4時,x2>3=x1,則
在區間(-∞,3)上,f `(x)<0, f (x)為減函數;
在區間(3,―a―1)上,f `(x)>0,f (x)為增函數;
在區間(―a―1,+∞)上,f `(x)<0,f (x)為減函數.
當a>-4時,x2<3=x1,則
在區間(-∞,―a―1)上,f `(x)<0, f (x)為減函數;
在區間(―a―1,3)上,f `(x)>0,f (x)為增函數;
在區間(3,+∞)上,f `(x)<0,f (x)為減函數.
(Ⅱ)由(Ⅰ)知,當a>0時,f (x)在區間(0,3)上的單調遞增,在區間(3,4)上單調遞減,那么f (x)在區間[0,4]上的值域是[min(f (0),f (4) ),f (3)],
而f (0)=-(2a+3)e3<0,f (4)=(2a+13)e-1>0,f (3)=a+6,
那么f (x)在區間[0,4]上的值域是[-(2a+3)e3,a+6].
又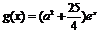 在區間[0,4]上是增函數,
在區間[0,4]上是增函數,
且它在區間[0,4]上的值域是[a2+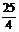 ,(a2+
,(a2+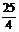 )e4],
)e4],
由于(a2+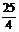 )-(a+6)=a2-a+
)-(a+6)=a2-a+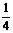 =(
=(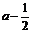 )2≥0,所以只須僅須
)2≥0,所以只須僅須
(a2+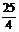 )-(a+6)<1且a>0,解得0<a<
)-(a+6)<1且a>0,解得0<a<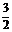 .
.
故a的取值范圍是(0,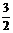 ).
).
例14 (2007年全國二)
已知函數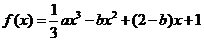
在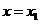 處取得極大值,在
處取得極大值,在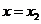 處取得極小值,且
處取得極小值,且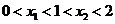 .
.
(1)證明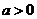 ;
;
(2)若z=a+2b,求z的取值范圍。
[解答過程]求函數 的導數
的導數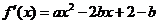 .
.
(Ⅰ)由函數 在
在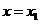 處取得極大值,在
處取得極大值,在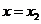 處取得極小值,知
處取得極小值,知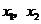 是
是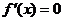 的兩個根.
的兩個根.
所以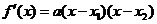
當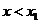 時,
時, 為增函數,
為增函數,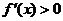 ,由
,由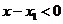 ,
,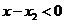 得
得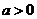 .
.
(Ⅱ)在題設下,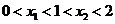 等價于
等價于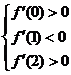 即
即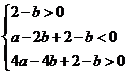 .
.
化簡得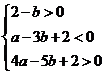 .
.
此不等式組表示的區域為平面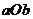 上三條直線:
上三條直線: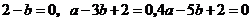 .
.
所圍成的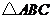 的內部,其三個頂點分別為:
的內部,其三個頂點分別為: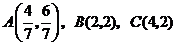 .
.
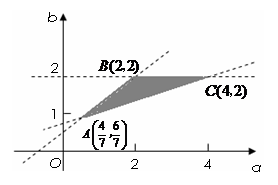
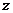 在這三點的值依次為
在這三點的值依次為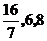 .
.
所以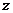 的取值范圍為
的取值范圍為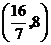 .
.
小結:本題的新穎之處在把函數的導數與線性
規劃有機結合.
考點4 導數的實際應用
建立函數模型,利用
典型例題
例15. (2007年重慶文)
用長為18 cm的鋼條圍成一個長方體形狀的框架,要求長方體的長與寬之比為2:1,問該長方體的長、寬、高各為多少時,其體積最大?最大體積是多少?
[考查目的]本小題主要考查函數、導數及其應用等基本知識,考查運用數學知識分析和解決實際問題的能力.
[解答過程]設長方體的寬為x(m),則長為2x(m),高為
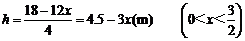 .
.
故長方體的體積為
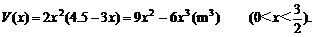
從而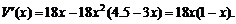
令V′(x)=0,解得x=0(舍去)或x=1,因此x=1.
當0<x<1時,V′(x)>0;當1<x<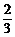 時,V′(x)<0,
時,V′(x)<0,
故在x=1處V(x)取得極大值,并且這個極大值就是V(x)的最大值。
從而最大體積V=V′(x)=9×12-6×13(m3),此時長方體的長為2 m,高為1.5 m.
答:當長方體的長為2 m時,寬為1 m,高為1.5 m時,體積最大,最大體積為3 m3。
例16.(2006年福建卷)統計表明,某種型號的汽車在勻速行駛中每小時的耗
油量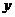 (升)關于行駛速度
(升)關于行駛速度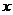 (千米/小時)的函數解析式可以表示為:
(千米/小時)的函數解析式可以表示為:
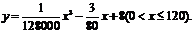 已知甲、乙兩地相距100千米.
已知甲、乙兩地相距100千米.
(I)當汽車以40千米/小時的速度勻速行駛時,從甲地到乙地要耗油多少升?
(II)當汽車以多大的速度勻速行駛時,從甲地到乙地耗油最少?最少為多少升?
[考查目的]本小題主要考查函數、導數及其應用等基本知識,考查運用數學知識分析和解決實際問題的能力.
[解答過程](I)當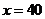 時,汽車從甲地到乙地行駛了
時,汽車從甲地到乙地行駛了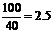 小時,
小時,
要耗沒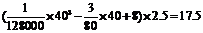 (升).
(升).
答:當汽車以40千米/小時的速度勻速行駛時,從甲地到乙地耗油17.5升。
(II)當速度為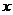 千米/小時時,汽車從甲地到乙地行駛了
千米/小時時,汽車從甲地到乙地行駛了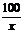 小時,設耗油量為
小時,設耗油量為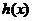 升,依題意得
升,依題意得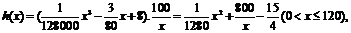
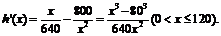
令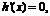 得
得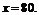
當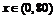 時,
時,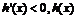 是減函數;當
是減函數;當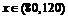 時,
時,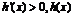 是增函數.
是增函數.
當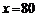 時,
時,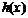 取到極小值
取到極小值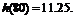
因為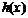 在
在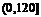 上只有一個極值,所以它是最小值.
上只有一個極值,所以它是最小值.
 答:當汽車以80千米/小時的速度勻速行駛時,從甲地到乙地耗油最少,最少為11.25升.
答:當汽車以80千米/小時的速度勻速行駛時,從甲地到乙地耗油最少,最少為11.25升.
考點1 導數的概念
對概念的要求:了解導數概念的實際背景,掌握導數在一點處的定義和導數的幾何意義,理解導函數的概念.
例1.(2007年北京卷)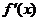 是
是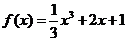 的導函數,則
的導函數,則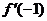 的值是 .
的值是 .
[考查目的] 本題主要考查函數的導數和計算等基礎知識和能力.
[解答過程] 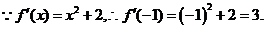
故填3.
例2. ( 2006年湖南卷)設函數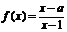 ,集合M=
,集合M=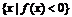 ,P=
,P=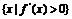 ,若M
,若M P,則實數a的取值范圍是 ( )
P,則實數a的取值范圍是 ( )
A.(-∞,1) B.(0,1) C.(1,+∞) D. [1,+∞)
[考查目的]本題主要考查函數的導數和集合等基礎知識的應用能力.
[解答過程]由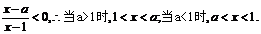
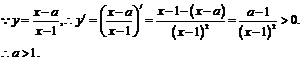
綜上可得M P時,
P時, 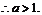
考點2 曲線的切線
(1)關于曲線在某一點的切線
求曲線y=f(x)在某一點P(x,y)的切線,即求出函數y=f(x)在P點的導數就是曲線在該點的切線的斜率.
(2)關于兩曲線的公切線
若一直線同時與兩曲線相切,則稱該直線為兩曲線的公切線.
典型例題
例3.(2007年湖南文)已知函數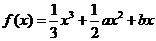 在區間
在區間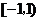 ,
,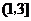 內各有一個極值點.
內各有一個極值點.
(I)求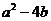 的最大值;
的最大值;
(II)當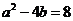 時,設函數
時,設函數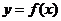 在點
在點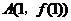 處的切線為
處的切線為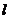 ,若
,若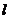 在點
在點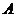 處穿過函數
處穿過函數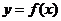 的圖象(即動點在點
的圖象(即動點在點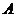 附近沿曲線
附近沿曲線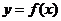 運動,經過點
運動,經過點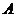 時,從
時,從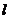 的一側進入另一側),求函數
的一側進入另一側),求函數 的表達式.
的表達式.
思路啟迪:用求導來求得切線斜率.
解答過程:(I)因為函數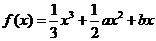 在區間
在區間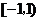 ,
,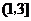 內分別有一個極值點,所以
內分別有一個極值點,所以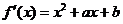
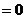 在
在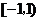 ,
,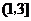 內分別有一個實根,
內分別有一個實根,
設兩實根為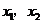 (
(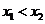 ),則
),則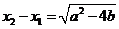 ,且
,且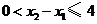 .于是
.于是
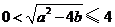 ,
,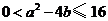 ,且當
,且當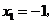
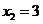 ,即
,即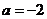 ,
,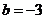 時等號成立.故
時等號成立.故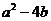 的最大值是16.
的最大值是16.
(II)解法一:由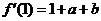 知
知 在點
在點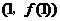 處的切線
處的切線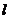 的方程是
的方程是
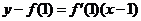 ,即
,即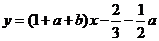 ,
,
因為切線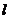 在點
在點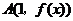 處空過
處空過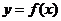 的圖象,
的圖象,
所以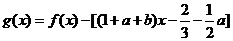 在
在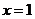 兩邊附近的函數值異號,則
兩邊附近的函數值異號,則
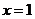 不是
不是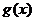 的極值點.
的極值點.
而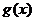
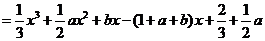 ,且
,且
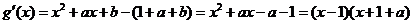 .
.
若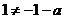 ,則
,則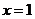 和
和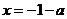 都是
都是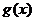 的極值點.
的極值點.
所以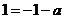 ,即
,即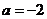 ,又由
,又由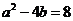 ,得
,得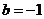 ,故
,故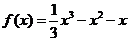 .
.
解法二:同解法一得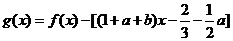
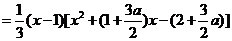 .
.
因為切線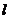 在點
在點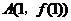 處穿過
處穿過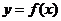 的圖象,所以
的圖象,所以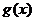 在
在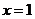 兩邊附近的函數值異號,于是存在
兩邊附近的函數值異號,于是存在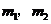 (
(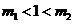 ).
).
當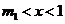 時,
時,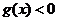 ,當
,當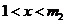 時,
時,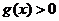 ;
;
或當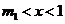 時,
時,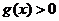 ,當
,當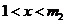 時,
時,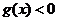 .
.
設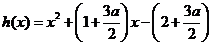 ,則
,則
當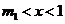 時,
時,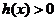 ,當
,當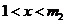 時,
時,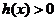 ;
;
或當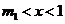 時,
時,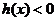 ,當
,當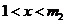 時,
時,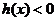 .
.
由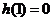 知
知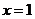 是
是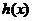 的一個極值點,則
的一個極值點,則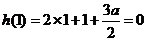 ,
,
所以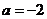 ,又由
,又由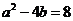 ,得
,得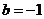 ,故
,故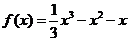 .
.
例4.(2006年安徽卷)若曲線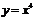 的一條切線
的一條切線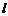 與直線
與直線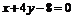 垂直,則
垂直,則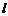 的方程為( )
的方程為( )
A.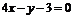 B.
B.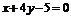
C.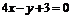 D.
D.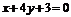
[考查目的]本題主要考查函數的導數和直線方程等基礎知識的應用能力.
[解答過程]與直線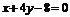 垂直的直線
垂直的直線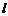 為
為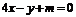 ,即
,即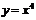 在某一點的導數為4,而
在某一點的導數為4,而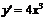 ,所以
,所以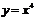 在(1,1)處導數為4,此點的切線為
在(1,1)處導數為4,此點的切線為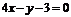 .
.
故選A.
例5. ( 2006年重慶卷)過坐標原點且與x2+y2 -4x+2y+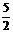 =0相切的直線的方程為 ( )
=0相切的直線的方程為 ( )
A.y=-3x或y=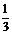 x B. y=-3x或y=-
x B. y=-3x或y=-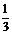 x C.y=-3x或y=-
x C.y=-3x或y=-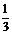 x D. y=3x或y=
x D. y=3x或y=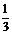 x
x
[考查目的]本題主要考查函數的導數和圓的方程、直線方程等基礎知識的應用能力.
[解答過程]解法1:設切線的方程為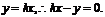
又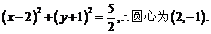
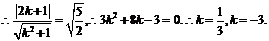
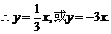
故選A.
解法2:由解法1知切點坐標為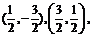 由
由
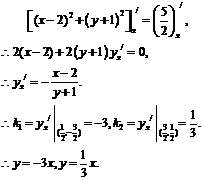
故選A.
例6.已知兩拋物線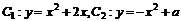 ,
, 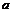 取何值時
取何值時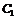 ,
,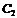 有且只有一條公切線,求出此時公切線的方程.
有且只有一條公切線,求出此時公切線的方程.
思路啟迪:先對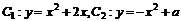 求導數.
求導數.
解答過程:函數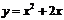 的導數為
的導數為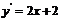 ,曲線
,曲線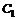 在點P(
在點P(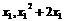 )處的切線方程為
)處的切線方程為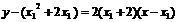 ,即
,即
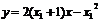 ①
①
曲線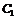 在點Q
在點Q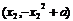 的切線方程是
的切線方程是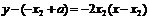 即
即
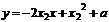 ②
②
若直線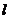 是過點P點和Q點的公切線,則①式和②式都是
是過點P點和Q點的公切線,則①式和②式都是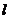 的方程,故得
的方程,故得
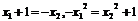 ,消去
,消去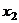 得方程,
得方程,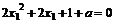
若△=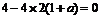 ,即
,即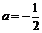 時,解得
時,解得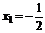 ,此時點P、Q重合.
,此時點P、Q重合.
∴當時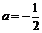 ,
,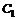 和
和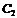 有且只有一條公切線,由①式得公切線方程為
有且只有一條公切線,由①式得公切線方程為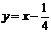 .
.
考點3 導數的應用
中學階段所涉及的初等函數在其定義域內都是可導函數,導數是研究函數性質的重要而有力的工具,特別是對于函數的單調性,以“導數”為工具,能對其進行全面的分析,為我們解決求函數的極值、最值提供了一種簡明易行的方法,進而與不等式的證明,討論方程解的情況等問題結合起來,極大地豐富了中學數學思想方法.復習時,應高度重視以下問題:
1.. 求函數的解析式; 2. 求函數的值域; 3.解決單調性問題; 4.求函數的極值(最值);
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com