
5.雙曲線的標準方程及其幾何性質:
|
標準方程 |
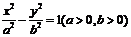 |
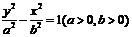 |
|
圖形 |
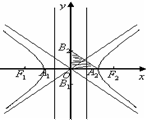 |
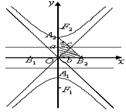 |
|
頂點 |
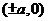 |
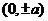 |
|
對稱軸 |
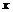 軸, 軸,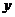 軸,實軸長為 軸,實軸長為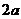 ,虛軸長為 ,虛軸長為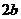 |
|
|
焦點 |
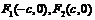 |
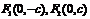 |
|
焦距 |
焦距為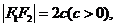 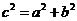 |
|
|
離心率 |
 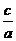 (e>1) (e>1) |
|
|
準線方程 |
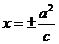 |
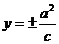 |
4.雙曲線的定義:
第一定義:平面內到兩個定點F1、F2的距離之差的絕對值等于定值2a(0<2a<|F1F2|)的點的軌跡叫做雙曲線,這兩個定點叫做雙曲線的焦點,兩焦點的距離叫做雙曲線的焦距.
第二定義: 平面內到定點F與到定直線l的距離之比是常數e(e>1)的點的軌跡是雙曲線,定點叫做雙曲線的焦點,定直線 叫做雙曲線的準線,常數
叫做雙曲線的準線,常數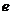 叫做雙曲線的離心率.
叫做雙曲線的離心率.
3.橢圓知識網絡
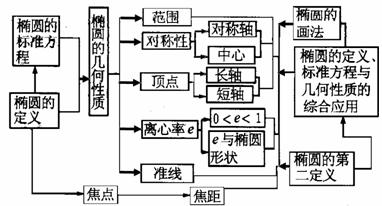
2.橢圓的標準方程及其幾何性質:
|
標準方程 |
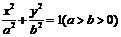 |
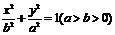 |
|
圖形 |
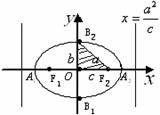 |
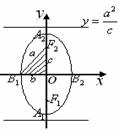 |
|
頂點 |
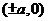 , ,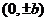 |
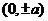 , ,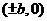 |
|
對稱軸 |
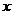 軸, 軸,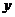 軸,長軸長為 軸,長軸長為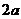 ,短軸長為 ,短軸長為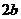 |
|
|
焦點 |
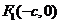 、 、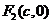 |
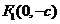 、 、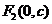 |
|
焦距 |
焦距為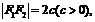 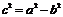 |
|
|
離心率 |
 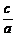 (0<e<1) (0<e<1) |
|
|
準線方程 |
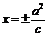 |
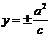 |
1.橢圓的定義:
第一定義:平面內到兩個定點F1、F2的距離之和等于定值2a(2a>|F1F2|)的點的軌跡叫做橢圓,這兩個定點叫做橢圓的焦點,兩焦點的距離叫做橢圓的焦距.
第二定義: 平面內到定點F與到定直線l的距離之比是常數e(0<e<1)的點的軌跡是橢圓,定點叫做橢圓的焦點,定直線 叫做橢圓的準線,常數
叫做橢圓的準線,常數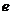 叫做橢圓的離心率.
叫做橢圓的離心率.
(二)考點預測題
1.(2008年山東卷,數學理科,4)設函數f(x)=|x+1|+|x-a|的圖象關于直線x=1對稱,則a的值為
(A) 3 (B)2 (C)1 (D)-1
[解析]本題考查函數的性質,函數的性質是重點考查內容,對函數的幾個性質應熟練掌握,09高考必將有涉及函數性質的題目出現,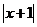 、
、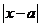 在數軸上表示點
在數軸上表示點 到點
到點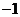 、
、 的距離,他們的和
的距離,他們的和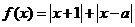 關于
關于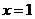 對稱,因此點
對稱,因此點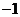 、
、 關于
關于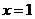 對稱,所以
對稱,所以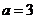 (直接去絕對值化成分段函數求解比較麻煩,如取特殊值解也可以)
(直接去絕對值化成分段函數求解比較麻煩,如取特殊值解也可以)
[答案]A
2.(2008年上海卷,數學文科,9)若函數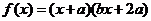 (常數
(常數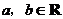 )是偶函數,且它的值域為
)是偶函數,且它的值域為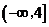 ,則該函數的解析式
,則該函數的解析式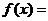 .
.
 [解析]本題考查函數的解析式,
[解析]本題考查函數的解析式,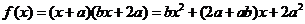 是偶函數,則其圖象關于y軸對稱,
是偶函數,則其圖象關于y軸對稱, 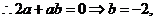
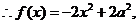 且值域為
且值域為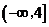 ,
, 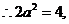
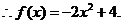
[答案]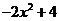
3.(2008年廣東卷,數學理科,19)設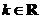 ,函數
,函數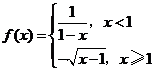 ,
,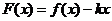 ,
,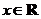 ,試討論函數
,試討論函數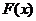 的單調性.
的單調性.
[解析]本題考查函數的綜合應用,廣東連續兩年均考查了函數解答題,江蘇08年也以函數作為壓軸題,應引起一定重視。
[答案]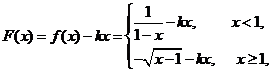
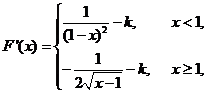
對于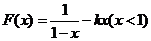 ,
,
當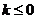 時,函數
時,函數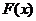 在
在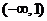 上是增函數;
上是增函數;
當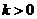 時,函數
時,函數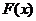 在
在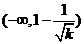 上是減函數,在
上是減函數,在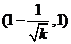 上是增函數;
上是增函數;
 對于
對于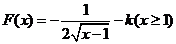 ,
,
當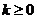 時,函數
時,函數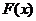 在
在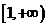 上是減函數;
上是減函數;
當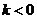 時,函數
時,函數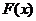 在
在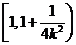 上是減函數,在
上是減函數,在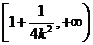 上是增函數。
上是增函數。

(一)文字介紹
本節內容在高考中占有一定比重,而且二分法是新增內容,應引起重視,同時對反函數的考查要求降低,本節多數題目將會以小題目出現,重點仍將是考查函數的性質,二分法,函數的定義域,以及函數的綜合應用等知識點。
6.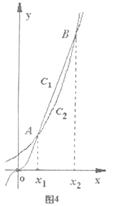 (山東省濟寧市2009屆高三11月教學質量檢測,數學理科,20)函數
(山東省濟寧市2009屆高三11月教學質量檢測,數學理科,20)函數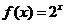 和
和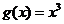 的圖象的示意圖如圖4所示,設兩函數的圖象交于點
的圖象的示意圖如圖4所示,設兩函數的圖象交于點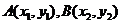 ,且
,且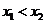
(1)請指出示意圖中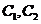 分別對應哪一個函數?
分別對應哪一個函數?
(2)若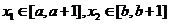 ,
,
且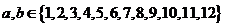 ,指出a,b的值,并說明理由;
,指出a,b的值,并說明理由;
(3)結合函數圖象的示意圖,判斷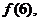
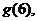
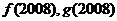 的大小,并按從小到大的順序排列。
的大小,并按從小到大的順序排列。
[解析]考查函數的綜合運用
[答案](1)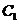 對應的函數為
對應的函數為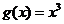 ,
,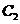 對應的函數為
對應的函數為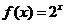
(2)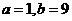
理由如下:
令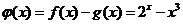 ,則
,則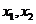 為函數
為函數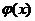 的零點。
的零點。
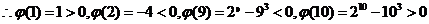 ,
,
 方程
方程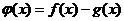 的兩個零點
的兩個零點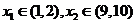
因此整數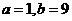
(3)從圖像上可以看出,當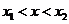 時,
時,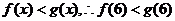
當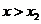 時,
時,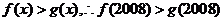
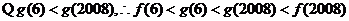
5.(安徽省六校2009年高三聯考試卷,數學文科,11)己知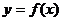 是偶函數,當
是偶函數,當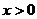 時,
時,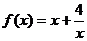 ,且當
,且當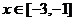 時
時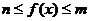 恒成立,則
恒成立,則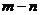 的最小值是( )
的最小值是( )
A 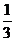 B
B 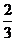 C 1
D
C 1
D 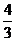
[解析]本題考查函數的性質及函數在給定區間上的最值,當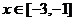 時,
時,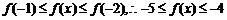 ,故
,故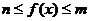 恒成立,則
恒成立,則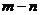 的最小值是1
的最小值是1
[答案]C
4.(遼寧省沈陽二中2008-2009學年上學期高三期中考試,數學,8)定義在[-2,2]上的偶函數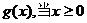 時,
時, 單調遞減,若
單調遞減,若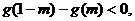 則實數m的取值范圍是
。
則實數m的取值范圍是
。
[解析]本題考查函數的性質,奇偶性,單調性的應用,由題意可知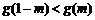 故
故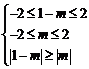 解得
解得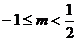
[答案]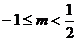
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com