
2.(2008全國二21).(本小題滿分12分)
設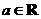 ,函數
,函數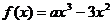 .
.
(Ⅰ)若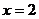 是函數
是函數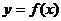 的極值點,求
的極值點,求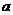 的值;
的值;
(Ⅱ)若函數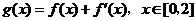 ,在
,在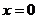 處取得最大值,求
處取得最大值,求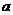 的取值范圍.
的取值范圍.
解:(Ⅰ)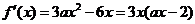 .
.
因為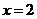 是函數
是函數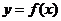 的極值點,所以
的極值點,所以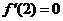 ,即
,即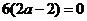 ,因此
,因此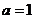 .
.
經驗證,當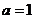 時,
時,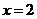 是函數
是函數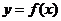 的極值點.············· 4分
的極值點.············· 4分
(Ⅱ)由題設,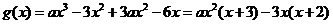 .
.
當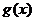 在區間
在區間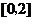 上的最大值為
上的最大值為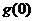 時,
時,
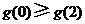 , 即
, 即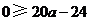 .故得
.故得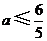 .··············· 9分
.··············· 9分
反之,當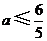 時,對任意
時,對任意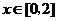 ,
,
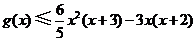
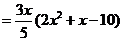
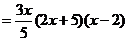
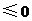 ,
,
而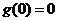 ,故
,故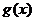 在區間
在區間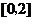 上的最大值為
上的最大值為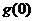 .
.
綜上,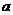 的取值范圍為
的取值范圍為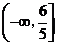 .······················ 12分
.······················ 12分
1.(2008全國一21).(本小題滿分12分)(注意:在試題卷上作答無效)
已知函數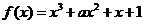 ,
,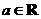 .
.
(Ⅰ)討論函數 的單調區間;
的單調區間;
(Ⅱ)設函數 在區間
在區間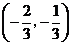 內是減函數,求
內是減函數,求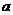 的取值范圍.
的取值范圍.
解:(1)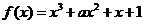
求導: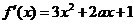
當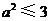 時,
時, ,
,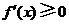
 在
在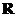 上遞增
上遞增
當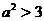 ,
,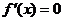 求得兩根為
求得兩根為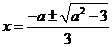
即 在
在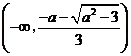 遞增,
遞增,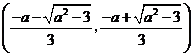 遞減,
遞減,
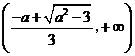 遞增
遞增
(2)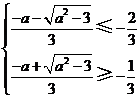 ,且
,且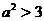 解得:
解得: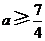
3.理解可導函數的單調性與其導數的關系;了解可導函數在某點取得極值的必要條件和充分條件(導數在極值點兩側異號);會求一些實際問題(一般指單峰函數)的最大值和最小值.
2.熟記基本導數公式;掌握兩個函數和、差、積、商的求導法則.了解復合函數的求導法則,會求某些簡單函數的導數.
導數屬于新增內容,是高中數學知識的一個重要的交匯點,命題范圍非常廣泛,為高考考查函數提供了廣闊天地,處于一種特殊的地位,不但一定出大題而相應有小題出現。主要考查導數有關的概念、計算和應用。利用導數工具研究函數的有關性質,把導數應用于單調性、極值等傳統、常規問題的同時,進一步升華到處理與自然數有關的不等式的證明,是函數知識和不等式知識的一個結合體,它的解題又融合了轉化、分類討論、函數與方程、數形結合等數學思想與方法,不但突出了能力的考查,同時也注意了高考重點與熱點,這一切對考查考生的應用能力和創新意識都大有益處。
1.了解導數概念的某些實際背景(如瞬時速度、加速度、光滑曲線切線的斜率等);掌握函數在一點處的導數的定義和導數的幾何意義;理解導函數的概念.
(二)考點預測題
1. (2007年山東高考真題模擬試卷八,理科,22)
橢圓G: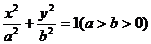 的兩個焦點F1(-c,0)、F2(c,0),M是橢圓上的
的兩個焦點F1(-c,0)、F2(c,0),M是橢圓上的
一點,且滿足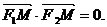
(Ⅰ)求離心率e的取值范圍;
(Ⅱ)當離心率e取得最小值時,點N(0,3)到橢圓上的點的最遠距離為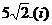 求此時
求此時
橢圓G的方程;(ⅱ)設斜率為k(k≠0)的直線l與橢圓G相交于不同的兩點A、B,Q
為AB的中點,問A、B兩點能否關于過點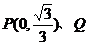 的直線對稱?若能,求出k的取值
的直線對稱?若能,求出k的取值
范圍;若不能,請說明理由.
[答案](I)設M(x0,y0)
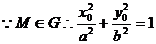 ①
①
又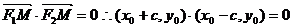 ②
②
由②得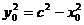 代入①式整理得
代入①式整理得 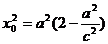
又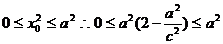
解得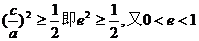
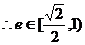
(Ⅱ)(i)當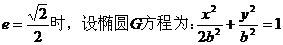
設H(x,y)為橢圓上一點,則
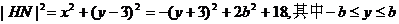
若0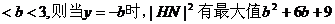
由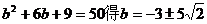 (舍去)
(舍去)
若b≥3,當y=-3時,|HN|2有最大值2b2+18
由2b2+18=50得b2=16
∴所求橢圓方程為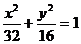
(ii)設A(x1,y1),B(x2,y2),Q(x0,y0),則由
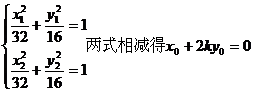 ③
③
又直線PQ⊥直線l ∴直線PQ方程為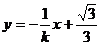
將點Q(x0,y0)代入上式得,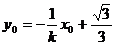 ④
④
由③④得Q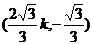
(解1)而Q點必在橢圓內部 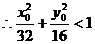
由此得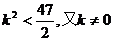

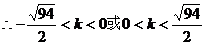
故當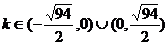 時A、B兩點關于點P、Q的直線對稱.
時A、B兩點關于點P、Q的直線對稱.
(解2)∴AB所在直線方程為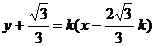
由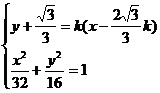 得
得
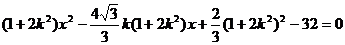
顯然1+2k2≠0
而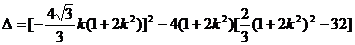
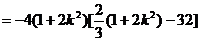
直線l與橢圓有兩不同的交點A、B ∴△>0
解得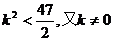
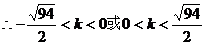
故當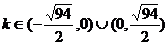 時,A、B兩點關于點P、Q的直線對稱。
時,A、B兩點關于點P、Q的直線對稱。
(ii)另解;設直線l的方程為y=kx+b
 由
由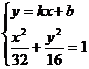 得
得
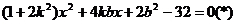
設A(x1,y1),B(x2,y2),Q(x0,y0),則
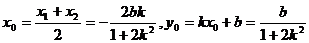 ③
③
又直線PQ⊥直線l ∴直線PQ方程為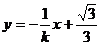
將點Q(x0,y0)代入上式得,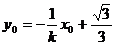 ④
④
將③代入④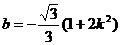 ⑤
⑤
∵x1,x2是(*)的兩根
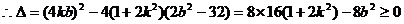 ⑥
⑥
⑤代入⑥得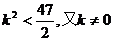
∴當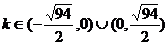 時,A、B兩點關于點P、Q的直線對稱
時,A、B兩點關于點P、Q的直線對稱
2.(2007年山東高考真題模擬試卷十一,理科,22)
雙曲線M的中心在原點,并以橢圓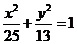 的焦點為焦點,以拋物線
的焦點為焦點,以拋物線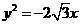 的
的
準線為右準線.
(Ⅰ)求雙曲線M的方程;
(Ⅱ)設直線 :
: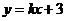 與雙曲線M相交于A、B兩點,O是原點.
與雙曲線M相交于A、B兩點,O是原點.
① 當 為何值時,使得
為何值時,使得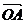
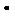
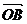
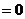 ?
?
② 是否存在這樣的實數 ,使A、B兩點關于直線
,使A、B兩點關于直線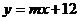 對稱?若存在,求出
對稱?若存在,求出 的值;若不存在,說明理由.
的值;若不存在,說明理由.
[答案](Ⅰ)易知,橢圓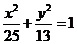 的半焦距為:
的半焦距為: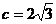 ,
,
又拋物線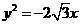 的準線為:
的準線為: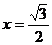 .
.
設雙曲線M的方程為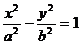 ,依題意有
,依題意有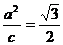 ,
,
故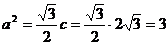 ,又
,又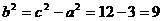 .
.
∴雙曲線M的方程為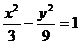 .
.
(Ⅱ)設直線 與雙曲線M的交點為
與雙曲線M的交點為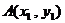 、
、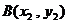 兩點
兩點
聯立方程組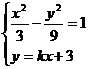 消去y得
消去y得 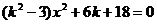 ,
,
 ∵
∵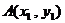 、
、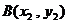 兩點的橫坐標是上述方程的兩個不同實根, ∴
兩點的橫坐標是上述方程的兩個不同實根, ∴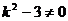
∴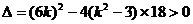
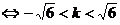 ,從而有
,從而有
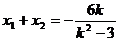 ,
,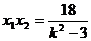 .
.
又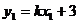 ,
,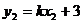
∴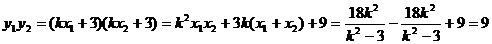 .
.
① 若
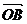
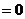 ,則有
,則有 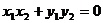 ,即
,即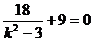
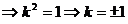 .
.
∴當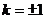 時,使得
時,使得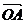
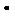
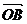
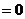 .
.
② 若存在實數 ,使A、B兩點關于直線
,使A、B兩點關于直線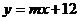 對稱,則必有
對稱,則必有 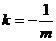 ,
,
因此,當m=0時,不存在滿足條件的k;
當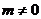 時,由
時,由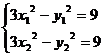 得
得 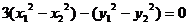
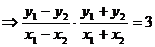
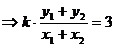
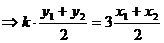
∵A、B中點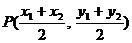 在直線
在直線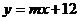 上,
上,
∴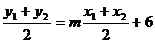 代入上式得
代入上式得
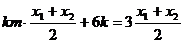
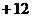 ;又
;又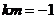 , ∴
, ∴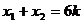
將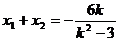 代入并注意到
代入并注意到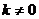 ,得
,得 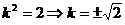 .
.
∴當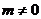 時,存在實數
時,存在實數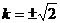 ,使A、B兩點關于直線
,使A、B兩點關于直線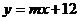 對稱.
對稱.
3.(2008年山東卷,理科,22)
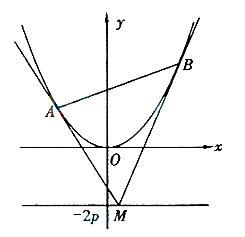 如圖,設拋物線方程為
如圖,設拋物線方程為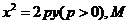 為直線
為直線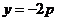 上任意一點,過
上任意一點,過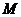 引拋物線的切線,切點分別為
引拋物線的切線,切點分別為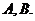
(I)求證: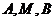 三點的橫坐標成等差數列;
三點的橫坐標成等差數列;
(II)已知當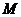 點的坐標為
點的坐標為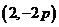 時,
時,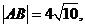 求此時拋物線的方程;
求此時拋物線的方程;
(III)是否存在點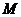 ,使得點
,使得點 關于直線
關于直線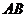 的對稱點
的對稱點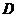 在拋物線
在拋物線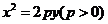 上,其中點
上,其中點 滿足
滿足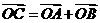 (
(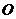 為坐標原點)。若存在,求出所有適合題意的點的坐標;若不存在,請說明理由。
為坐標原點)。若存在,求出所有適合題意的點的坐標;若不存在,請說明理由。
[答案](I)證明:由題意設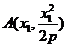 ,
,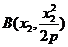 ,
,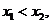
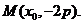
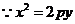 ,
,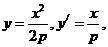
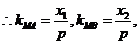
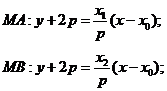

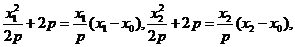
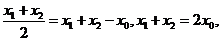
所以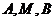 三點的橫坐標成等差數列。
三點的橫坐標成等差數列。
(II)解:由(I)知,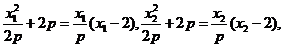
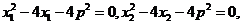
所以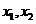 是方程
是方程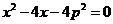 的兩根,
的兩根,
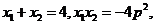
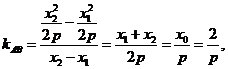
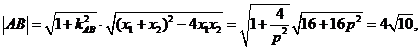
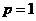 或
或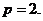
因此所求拋物線方程為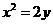 或
或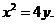
(III)解:設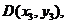 由題意得
由題意得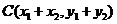 ,則
,則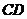 中點坐標為
中點坐標為
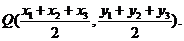
設直線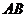 的方程為
的方程為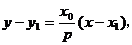
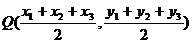 與
與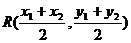 都在
都在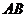 上,代入得
上,代入得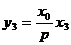 .
.
若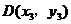 在拋物線上,則
在拋物線上,則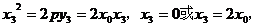 即
即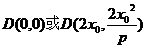 .
.
1)當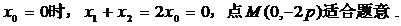
2)當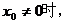
(1)對于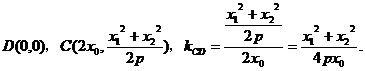
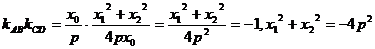 矛盾.
矛盾.
(2)對于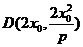 ,
,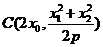 ,則
,則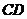 與
與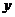 軸平行,而
軸平行,而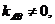 直線
直線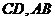 不垂直矛盾。
不垂直矛盾。
綜上可知,僅存在一點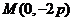 適合題意.
適合題意.
(一)文字介紹
圓錐曲線是解析幾何的核心內容,也是高考命題的熱點之一.高考對圓錐曲線的考查,總體上是以知識應用和問題探究為主,一般是給出曲線方程,討論曲線的基本元素和簡單的幾何性質;或給出曲線滿足的條件,判斷(求)其軌跡;或給出直線與曲線、曲線與曲線的位置關系,討論與其有關的其他問題(如直線的方程、直線的條數、弦長、曲線中參變量的取值范圍等);或考查圓錐曲線與其他知識綜合(如不等式、函數、向量、導數等)的問題等.
8. (遼寧省撫順一中2009屆高三第一次模擬考試,理科,21)
橢圓ax2+by2 =1與直線x+y-1=0相交于A、B兩點,若|AB|=2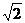 ,線段AB的中點為C,且OC的斜率為
,線段AB的中點為C,且OC的斜率為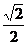 ,求橢圓方程.
,求橢圓方程.
[解析]聯立直線與橢圓方程,根據一元二次方程根與系數關系、中點坐標公式、斜率公式求出a,b的關系,再由弦長公式求出a,b的值,即得所求橢圓的方程.
[答案]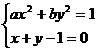 ∴(a+b)x2 -2bx+b-1=0
∴(a+b)x2 -2bx+b-1=0
∴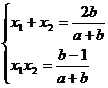
C(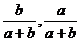 )
)
KOC =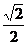 ∴b=
∴b=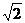 a,
a,
代入|AB|=2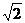 ,即:(1+k2)[(x1+x2)2-4 x1x2]=8
,即:(1+k2)[(x1+x2)2-4 x1x2]=8
a=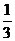 ,b=
,b=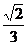
∴橢圓方程為: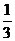 x2+
x2+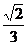 y2 =1
y2 =1
7. (江蘇省鹽城一中、大豐中學、建湖中學2009屆高三第二次調研考試, 21)
拋物線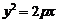 的準線的方程為
的準線的方程為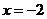 ,該拋物線上的每個點到準線
,該拋物線上的每個點到準線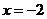 的距離都與到定點N的距離相等,圓N是以N為圓心,同時與直線
的距離都與到定點N的距離相等,圓N是以N為圓心,同時與直線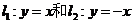 相切的圓,
相切的圓,
(Ⅰ)求定點N的坐標;
(Ⅱ)是否存在一條直線 同時滿足下列條件:
同時滿足下列條件:
①  分別與直線
分別與直線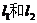 交于A、B兩點,且AB中點為
交于A、B兩點,且AB中點為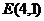 ;
;
②  被圓N截得的弦長為
被圓N截得的弦長為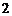 .
.
[解析](1)由拋物線的定義易得;
(2)假設存在直線 ,設出直線
,設出直線 的方程為
的方程為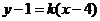 ,
,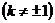 .
.
方法1:由弦心距的長為1求出 的值,然后檢驗是否符合AB中點為
的值,然后檢驗是否符合AB中點為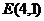 這個條件;
這個條件;
方法2:將直線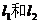 的方程分別與直線
的方程分別與直線 的方程聯立,求出A、B兩點的坐標,再由中點坐標公式求出
的方程聯立,求出A、B兩點的坐標,再由中點坐標公式求出 的值,最后檢驗弦心距的長是否為1;
的值,最后檢驗弦心距的長是否為1;
方法3:設出A點的坐標為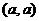 ,由中點坐標公式和B點在
,由中點坐標公式和B點在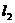 上,求出
上,求出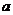 的值,進而求出直線
的值,進而求出直線 的斜率,最后檢驗弦心距的長是否為1.
的斜率,最后檢驗弦心距的長是否為1.
[答案](1)因為拋物線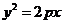 的準線的方程為
的準線的方程為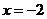
所以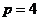 ,根據拋物線的定義可知點N是拋物線的焦點,
,根據拋物線的定義可知點N是拋物線的焦點,
所以定點N的坐標為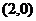
(2)假設存在直線 滿足兩個條件,顯然
滿足兩個條件,顯然 斜率存在,
斜率存在,
設 的方程為
的方程為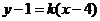 ,
,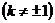
以N為圓心,同時與直線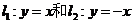 相切的圓N的半徑為
相切的圓N的半徑為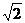 ,
,
方法1:因為 被圓N截得的弦長為2,所以圓心到直線的距離等于1,
被圓N截得的弦長為2,所以圓心到直線的距離等于1,
即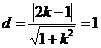 ,解得
,解得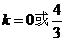 ,
,
當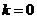 時,顯然不合AB中點為
時,顯然不合AB中點為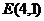 的條件,矛盾!
的條件,矛盾!
當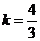 時,
時, 的方程為
的方程為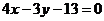
由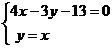 ,解得點A坐標為
,解得點A坐標為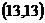 ,
,
由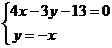 ,解得點B坐標為
,解得點B坐標為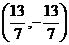 ,
,
顯然AB中點不是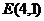 ,矛盾!
,矛盾!
所以不存在滿足條件的直線 .
.
方法2:由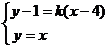 ,解得點A坐標為
,解得點A坐標為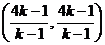 ,
,
由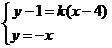 ,解得點B坐標為
,解得點B坐標為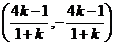 ,
,
因為AB中點為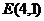 ,所以
,所以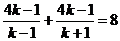 ,解得
,解得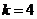 ,
,
所以 的方程為
的方程為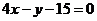 ,
,
圓心N到直線 的距離
的距離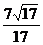 ,
,
因為 被圓N截得的弦長為2,所以圓心到直線的距離等于1,矛盾!
被圓N截得的弦長為2,所以圓心到直線的距離等于1,矛盾!
所以不存在滿足條件的直線 .
.
方法3:假設A點的坐標為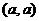 ,
,
因為AB中點為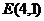 ,所以B點的坐標為
,所以B點的坐標為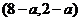 ,
,
又點B 在直線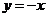 上,所以
上,所以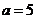 ,
,
所以A點的坐標為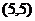 ,直線
,直線 的斜率為4,
的斜率為4,
所以 的方程為
的方程為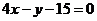 ,
,
圓心N到直線 的距離
的距離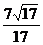 ,
,
因為 被圓N截得的弦長為2,所以圓心到直線的距離等于1,矛盾!
被圓N截得的弦長為2,所以圓心到直線的距離等于1,矛盾!
所以不存在滿足條件的直線 .
.
6. (山東省文登市2009屆高三第三次月考試題,理科,21)
過點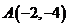 作傾斜角為
作傾斜角為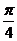 的直線,交拋物線
的直線,交拋物線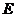 :
: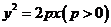 于
于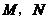 兩點,且
兩點,且
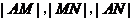 成等比數列。⑴求
成等比數列。⑴求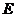 的方程;⑵過點
的方程;⑵過點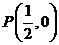 的直線
的直線 與曲線
與曲線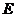 交于
交于

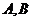 兩點。設
兩點。設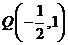 ,
,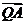 與
與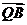 的夾角為
的夾角為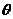 ,
,
求證: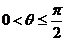 。
。
[解析]⑴設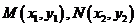 ,聯立直線與拋物線的方程
,聯立直線與拋物線的方程
后根據一元二次方程根與系數關系可得到關于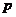 的方程,解之即得
的方程,解之即得
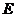 的方程;⑵法一:要證
的方程;⑵法一:要證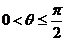 ,只需證明
,只需證明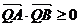 即可.
即可.
法二:根據“以拋物線焦點弦為直徑的圓與準線相切”這一性質分兩種情況討論即可得證.
[答案]⑴設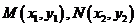 ,則由題
,則由題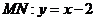 ,由
,由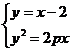 得
得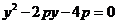 ,故
,故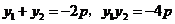 。
。
又根據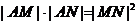 可得
可得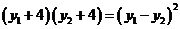 ,即
,即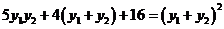 ,代入可得
,代入可得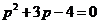 ,解得
,解得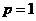 (舍負)。故
(舍負)。故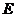 的方程為
的方程為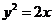 ;
;
⑵法一:設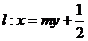 ,代入
,代入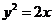 得
得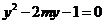 ,故
,故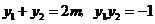 ,
,
從而
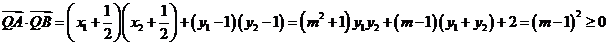 ,因此
,因此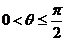
法二:顯然點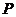 是拋物線
是拋物線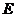 的焦點,點
的焦點,點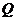 是其準線
是其準線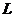 上一點。設
上一點。設 為
為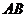 的中點,過
的中點,過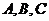 分別作
分別作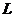 的垂線,垂足分別為
的垂線,垂足分別為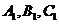 ,則
,則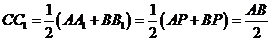 。因此以
。因此以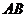 為直徑的圓與準線
為直徑的圓與準線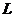 相切(于點
相切(于點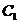 )。若
)。若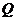 與
與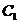 重合,則
重合,則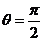 。否則點
。否則點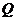 在
在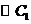 外,因此
外,因此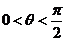 。綜上知
。綜上知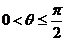 。
。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com