
5. (�����ʮ���^(q��)�h���c(di��n)�ЌW(xu��))��������������������������������������������������������
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
(�����ʮ���^(q��)�h���c(di��n)�ЌW(xu��))��������������������������������������������������������
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
(���}�M��14��)
��֪����(sh��)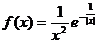
(��)�Д� ����ż�ԣ�
����ż�ԣ�
(��)��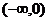 ����(sh��)
����(sh��) �ĘOֵ��
�ĘOֵ��
(��)��(sh��)�W(xu��)�w�{���C������(d��ng)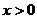 �r��������������(sh��)
�r��������������(sh��)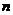 ����
����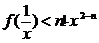
�⣺(��) 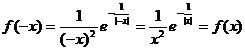
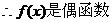 ������3��
������3��
(��)��(d��ng)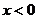 �r��
�r��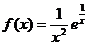 ��
��
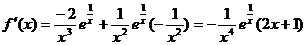 ������������������
������5��
������������������
������5��
��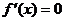 ��
��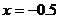 ��
��
���� ��(d��ng)x׃���r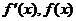 ��׃����r���±�:�� �ɱ���
��׃����r���±�:�� �ɱ���
֪��
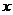 |
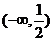 |
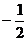 |
(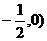 |
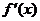 |
+ |
0 |
�� |
 |
�� |
�O��ֵ |
�p |
��(d��ng)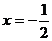 �r
�r ȡ�O��ֵ
ȡ�O��ֵ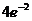 . ������������������������ ������7��
. ������������������������ ������7��
(��)��(d��ng)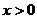 �r
�r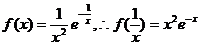 ������������
������8��
������������
������8��
�����]����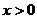 �r������ʽ
�r������ʽ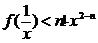 �ȃr��
�ȃr��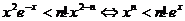 ��(1)
��(1)
������ֻҪ�Ô�(sh��)�W(xu��)�w�{���C������ʽ(1)��һ��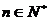 ���������ɡ�����9��
���������ɡ�����9��
(i)��(d��ng)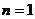 �r���O(sh��)
�r���O(sh��)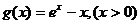
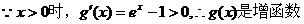 ���� �������� ������10��
���� �������� ������10��
��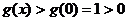 ����
����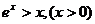
���ԣ���(d��ng)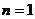 �r������ʽ(1)��������������������������
�� ������11��
�r������ʽ(1)��������������������������
�� ������11��
(ii)���O(sh��)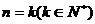 �r������ʽ(1)����������
�r������ʽ(1)����������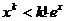
����(d��ng)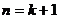 �r�O(sh��)
�r�O(sh��)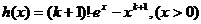
����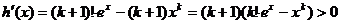 �� ������12��
�� ������12��
����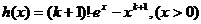 ��������(sh��)��
��������(sh��)��
�����ԣ�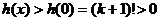 ����
����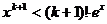 ������ ������13��
������ ������13��
�@�f����(d��ng)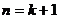 �r����ʽ(1)Ҳ��������
�r����ʽ(1)Ҳ��������
����(j��)(i)(ii)��֪����ʽ(1)��һ��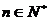 ��������
��������
��ԭ����ʽ��һ��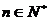 ������.��������������������������
���� ������14��
������.��������������������������
���� ������14��
4��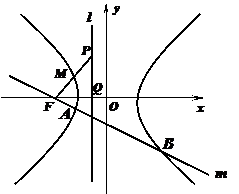 ��֪����(sh��)
��֪����(sh��) ����(sh��)��
����(sh��)�� ��ǰ
��ǰ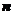 �(xi��ng)�͞�
�(xi��ng)�͞�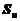 ��
��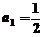 ����
����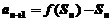
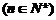 ��
��
(��)��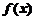 �����ֵ��
�����ֵ��
(��)�C����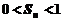 ��
��
(��)̽������(sh��)��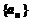 �Ƿ���{(di��o)��
�Ƿ���{(di��o)��
�⣺(��)��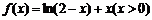 ����
����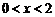 ��
��
��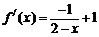 =
=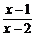 ��(2��)
��(2��)
�ஔ(d��ng)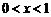 �r��
�r��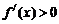 ��
��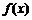 ��
��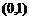 �φ��{(di��o)�f����
�φ��{(di��o)�f����
��(d��ng)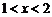 �r��
�r��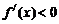 ��
��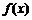 ��
��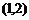 �φ��{(di��o)�f�p��
�φ��{(di��o)�f�p��
���څ^(q��)�g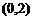 ��(n��i)��
��(n��i)��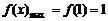 ��(2��)
��(2��)
(��)��(sh��)�W(xu��)�w�{���C����
���� ��(d��ng)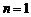 �r��
��
�r��
��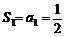 ����
����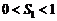 ��
��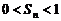 ������
������
�� ���O(sh��)��(d��ng)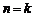 �r��
�r��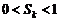 ������
������
��(d��ng)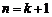 �r����
�r����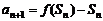 ��
��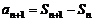 ����
����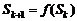 ��(2��)
��(2��)
��(��) ֪��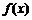 ��
��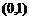 �φ��{(di��o)�f��������
�φ��{(di��o)�f��������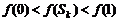 ��
��
��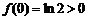 ��
��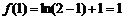 ��
��
��
��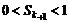 ��
��
�ஔ(d��ng)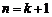 �r��
�r��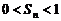 Ҳ������
Ҳ������
�ɢ١���֪��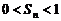 ������
������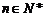 ��������(4��)
��������(4��)
(��)��(sh��)��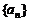 ���{(di��o)�f�p��(1��)
���{(di��o)�f�p��(1��)
�������£�
��(d��ng)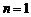 �r��
�r��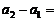
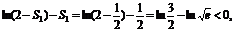 ��
��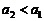 ��
��
��(d��ng)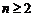 �r����
�r����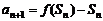 ��
��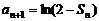 ��
��
��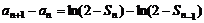
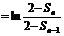 ��(2��)
��(2��)
���� (��) ֪��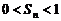 ����
����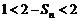 ��
��
��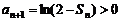 ����
����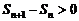
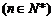
��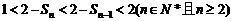 ��
��
��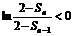 ����
����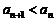 ��(3��)
��(3��)
�C�ϣ���(sh��)��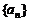 ���{(di��o)�f�p��
���{(di��o)�f�p��
3.(�㽭ʡ���c(di��n)�ЌW(xu��)2008��5��)
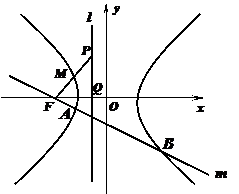 ��֪����(sh��)
��֪����(sh��)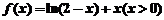 ����(sh��)��
����(sh��)��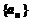 ��ǰ
��ǰ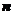 �(xi��ng)�͞�
�(xi��ng)�͞�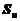 ��
��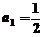 ����
����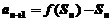
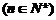 ��
��
(��)��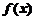 �����ֵ��
�����ֵ��
(��)�C����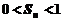 ��
��
(��)̽������(sh��)��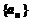 �Ƿ���{(di��o)��
�Ƿ���{(di��o)��
�⣺(��)��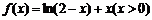 ����
����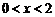 ��
��
��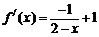 =
=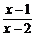 ��(2��)
��(2��)
�ஔ(d��ng)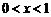 �r��
�r��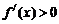 ��
��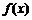 ��
��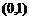 �φ��{(di��o)�f����
�φ��{(di��o)�f����
��(d��ng)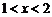 �r��
�r��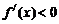 ��
��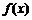 ��
��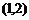 �φ��{(di��o)�f�p��
�φ��{(di��o)�f�p��
���څ^(q��)�g ��(n��i)��
��(n��i)��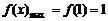 ��(2��)
��(2��)
(��)��(sh��)�W(xu��)�w�{���C����
���� ��(d��ng) �r��
��
�r��
��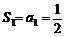 ����
����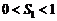 ��
��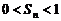 ������
������
�� ���O(sh��)��(d��ng)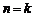 �r��
�r��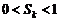 ������
������
��(d��ng)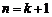 �r����
�r����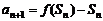 ��
��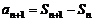 ����
����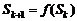 ��(2��)
��(2��)
��(��) ֪��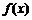 ��
��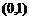 �φ��{(di��o)�f��������
�φ��{(di��o)�f��������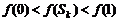 ��
��
��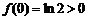 ��
�� ��
��
��
�� ��
��
�ஔ(d��ng) �r��
�r�� Ҳ������
Ҳ������
�ɢ١���֪�� ������
������ ��������(4��)
��������(4��)
(��)��(sh��)�� ���{(di��o)�f�p��(1��)
���{(di��o)�f�p��(1��)
�������£�
��(d��ng) �r��
�r��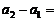
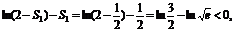 ��
��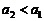 ��
��
��(d��ng)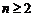 �r����
�r����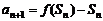 ��
��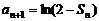 ��
��
��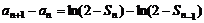
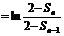 ��(2��)
��(2��)
���� (��) ֪��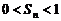 ����
����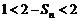 ��
��
��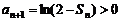 ����
����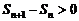
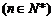
��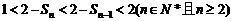 ��
��
��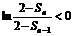 ����
����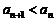 ��(3��)
��(3��)
�C�ϣ���(sh��)��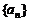 ���{(di��o)�f�p��
���{(di��o)�f�p��
2.(���ώ�����)(��С�}�M��14��)��֪����(sh��)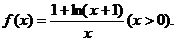
�� (��)ԇ�Дຯ��(sh��)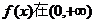 �φ��{(di��o)�Բ��C����ĽY(ji��)Փ��
�φ��{(di��o)�Բ��C����ĽY(ji��)Փ��
�� (��)��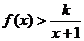 �������������(sh��)k�����ֵ��
�������������(sh��)k�����ֵ��
�� (��)���C��(1+1��2)(1+2��3)��[1+n(n+1)]>e2n��3.
���⣺(I)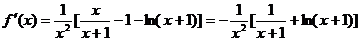 ��������(2��)
��������(2��)
���� 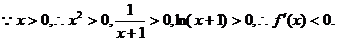
���� 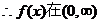 ���ǜp����(sh��).����������������������������������������(4��)
���ǜp����(sh��).����������������������������������������(4��)
���� (II)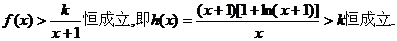
���� ��h(x)����Сֵ����k.��������������������������������������������(6��)
���� 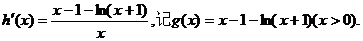
���� �t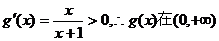 �φ��{(di��o)�f����
�φ��{(di��o)�f����
���� ��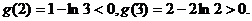
���� 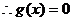 ����Ψһ��(sh��)��a���ҝM��
����Ψһ��(sh��)��a���ҝM��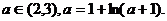
��(d��ng)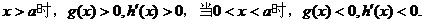
��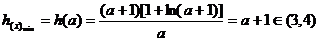
��������(sh��)k�����ֵ��3���� ����������������9��
(��)��(��)֪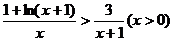
��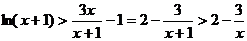 �� ������������11��
�� ������������11��
��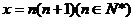 ���t
���t
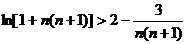
��l(xi��ng)n(1+1��2)+ln(1+2��3)+��+ln[1+n(n+1)]
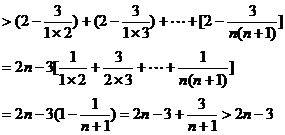
��(1+1��2)(1+2��3)��[1+n(n+1)]>e2n��3 ��������������14��
1.(2008��H���и����y(t��ng)һ��ԇ)
���x��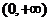 ����������(sh��)f(x)��g(x)��h(x),��֪f(x)=lnx,g(x)=
����������(sh��)f(x)��g(x)��h(x),��֪f(x)=lnx,g(x)= 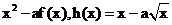 ,��g(x)��[1��2]��������(sh��)��h(x)��(0��1)��p����(sh��).
,��g(x)��[1��2]��������(sh��)��h(x)��(0��1)��p����(sh��).
(I)��g(x)��h(x)�ı��_(d��)ʽ��
(II)���C����(d��ng)1<x< 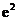 �r������
�r������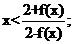
(III)��h(x)����(y��ng)������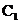 ����ƽ��6����λ�������
����ƽ��6����λ�������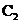 ����
����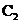 �cg(x)����(y��ng)����
�cg(x)����(y��ng)����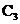 �Ľ��c(di��n)����(sh��)�����f������.
�Ľ��c(di��n)����(sh��)�����f������.
��(I)���}�⣺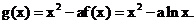
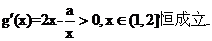
��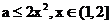 �����.
�����.

��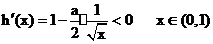 �����.
�����.
��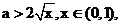 ��
��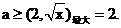
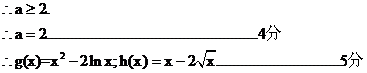
(II)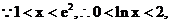
���C��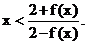
ֻ���C��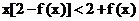
���C��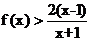
ӛ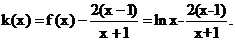
��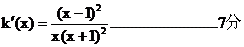
�ஔ(d��ng)x>1�r��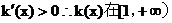 ��������(sh��)����������.9��
��������(sh��)����������.9��
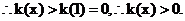
��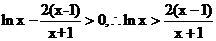
��Y(ji��)Փ����������������������������������������..10��
(III)�� (1)֪��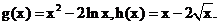
��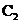 ����(y��ng)���_(d��)ʽ��
����(y��ng)���_(d��)ʽ��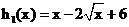
�����}�D(zhu��n)������(sh��)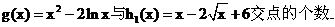
���̣�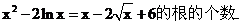
����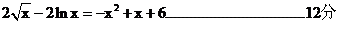
�O(sh��)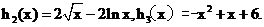
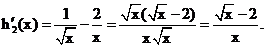
 �ஔ(d��ng)
�ஔ(d��ng)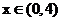 �r��
�r��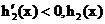 ��p����(sh��).
��p����(sh��).
 ��(d��ng)
��(d��ng)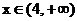 �r��
�r��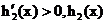 ��������(sh��).
��������(sh��).
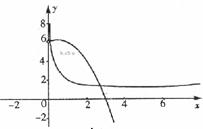
��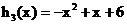 �ĈD���_�����µĒ��タ
�ĈD���_�����µĒ��タ
��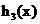 �c
�c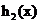 �Ĵ��D����D��
�Ĵ��D����D��
��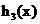 �c
�c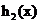 �Ľ��c(di��n)����(sh��)��2��.
�Ľ��c(di��n)����(sh��)��2��.
��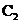 �c
�c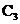 �Ľ��c(di��n)����(sh��)��2��.
�Ľ��c(di��n)����(sh��)��2��.
7.(2008������19)(���}�M��12��)
������֪����(sh��)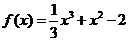 .
.
��(��)�O(sh��){an}������(sh��)�M�ɵĔ�(sh��)�У�ǰn�(xi��ng)�͞�Sn������a1=3.���c(di��n)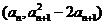 (n��N*)�ں���(sh��)y=f��(x)�ĈD���ϣ����C���c(di��n)(n,Sn)Ҳ��y=f��(x)�ĈD���ϣ�
(n��N*)�ں���(sh��)y=f��(x)�ĈD���ϣ����C���c(di��n)(n,Sn)Ҳ��y=f��(x)�ĈD���ϣ�
��(��)��(sh��)f(x)�څ^(q��)�g(a-1,a)��(n��i)�ĘOֵ.
��С�}��Ҫ���麯��(sh��)�Oֵ���Ȳ(sh��)�еȻ���֪�R���������c���ϡ��D(zhu��n)���c���w�Ȕ�(sh��)�W(xu��)˼�뷽��������������}�ͽ�Q���}������.�M��12��.
���� (��)�C������?y��n)?sub>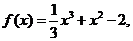 ����
����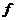 ��(x)=x2+2x,
��(x)=x2+2x,
���� ���c(di��n)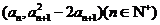 �ں���(sh��)y=f��(x)�ĈD����,
�ں���(sh��)y=f��(x)�ĈD����,
���� ��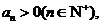 ����
����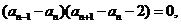
���� ����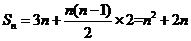 ,����?y��n)?sub>
,����?y��n)?sub>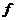 ��(n)=n2+2n,����
��(n)=n2+2n,����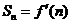 ,
,
���� ���c(di��n)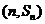 Ҳ�ں���(sh��)y=f��(x)�ĈD����.
Ҳ�ں���(sh��)y=f��(x)�ĈD����.
(��)��: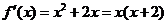 ,
,
��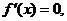 ��
��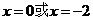 .
.
��(d��ng)x׃���r,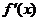 �p
�p ��׃����r���±�:
��׃����r���±�:
|
x |
(-��,-2) |
-2 |
(-2,0) |
0 |
(0,+��) |
|
f��(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
�J |
�O��ֵ |
�K |
�OСֵ |
�J |
ע�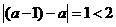 ,�Ķ�
,�Ķ�
�ٮ�(d��ng)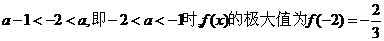 ,�˕r
,�˕r �o�OСֵ��
�o�OСֵ��
�ڮ�(d��ng)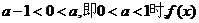 �ĘOСֵ��
�ĘOСֵ��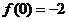 ,�˕r
,�˕r �o�O��ֵ��
�o�O��ֵ��
�ۮ�(d��ng)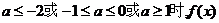 �ȟo�O��ֵ�֟o�OСֵ.
�ȟo�O��ֵ�֟o�OСֵ.
6.(2008�ؑc��20)(��С�}�M��13��.(��)С��5��.(��)С��8��.)
�����O(sh��)����(sh��)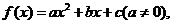 ����y=f(x)ͨ�^�c(di��n)(0��2a+3)�������c(di��n)(-1��f(-1))
����y=f(x)ͨ�^�c(di��n)(0��2a+3)�������c(di��n)(-1��f(-1))
̎���о���ֱ��y�S.
(��)��a�քe��ʾb��c��
(��)��(d��ng)bcȡ����Сֵ�r����(sh��)g(x)=-f(x)e-x�Ć��{(di��o)�^(q��)�g.
�⣺(��)��?y��n)?sub>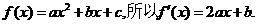
�������� ����?y��n)�����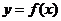 ͨ�^�c(di��n)(0��2a+3),
ͨ�^�c(di��n)(0��2a+3),
�������� ��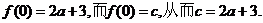
�������� ������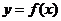 ��(-1��f(-1))̎���о���ֱ��y�S����
��(-1��f(-1))̎���о���ֱ��y�S����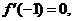
�������� ��-2a+b=0,���b=2a.
���� (��)��(��)��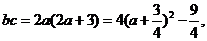
�������� �ʮ�(d��ng)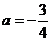 �r��
�r��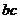 ȡ����Сֵ-
ȡ����Сֵ-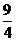 .
.
�������� �˕r��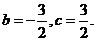
�������� �Ķ�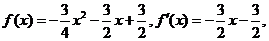
�������� 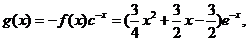
�������� ����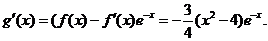
�������� ��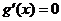 �����
�����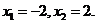
������ �� ��(d��ng)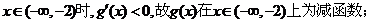
�������� ��(d��ng)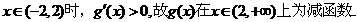
�������� ��(d��ng)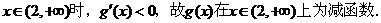
�������� �ɴ˿�Ҋ������(sh��) �Ć��{(di��o)�f�p�^(q��)�g��(-�ޣ�-2)��(2��+��)�����{(di��o)�f���^(q��)�g��(-2��2).
�Ć��{(di��o)�f�p�^(q��)�g��(-�ޣ�-2)��(2��+��)�����{(di��o)�f���^(q��)�g��(-2��2).
5..(2008�����21)��(���}�M��12��)
��֪����(sh��)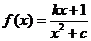 (
(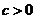 ��
��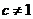 ��
��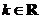 )ǡ��һ���O��ֵ�c(di��n)��һ���OСֵ�c(di��n)������һ����
)ǡ��һ���O��ֵ�c(di��n)��һ���OСֵ�c(di��n)������һ����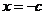 ��
��
(��)��(sh��) ����һ���Oֵ�c(di��n)��
����һ���Oֵ�c(di��n)��
(��)��(sh��) �ĘO��ֵ
�ĘO��ֵ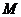 �͘OСֵ
�͘OСֵ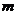 ������
������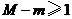 �r
�r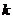 ��ȡֵ������
��ȡֵ������
�⣺(��)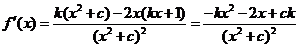 �����}��֪
�����}��֪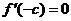 ��
��
����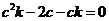 ��(*)
��(*)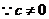 ��
��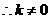 ��
��
��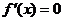 ��
��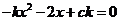 ��
��
���f�_(d��)����֪��һ���Oֵ�c(di��n)��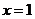 (��
(��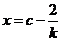 )��
)��
(��)��(*)ʽ��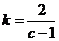 ����
����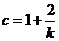 ��
��
��(d��ng)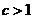 �r��
�r��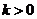 ����(d��ng)
����(d��ng)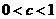 �r��
�r��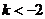 ��
��
(i)��(d��ng)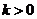 �r��
�r�� ��
��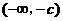 ��
��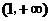 ��(n��i)�ǜp����(sh��)����
��(n��i)�ǜp����(sh��)����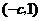 ��(n��i)��������(sh��)��
��(n��i)��������(sh��)��
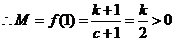 ��
��
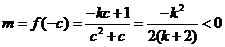 ��
��
��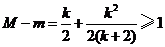 ��
��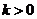 �����
�����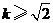 ��
��
(ii)��(d��ng)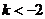 �r��
�r�� ��
��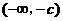 ��
��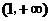 ��(n��i)��������(sh��)����
��(n��i)��������(sh��)����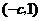 ��(n��i)�ǜp����(sh��)��
��(n��i)�ǜp����(sh��)��
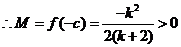 ��
��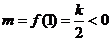
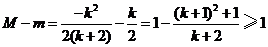 �������
�������
�C�Ͽ�֪������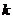 ��ȡֵ������
��ȡֵ������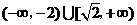 ��
��
4..(2008���Ͼ�21)(��С�}�M��13��)
��֪����(sh��)f(x)=ln2(1+x)-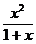 .
.
(I)�� ��(sh��) ���{(di��o)�^(q��)�g;
���{(di��o)�^(q��)�g;
(��)������ʽ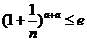 �������
�������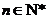 ������(����e����Ȼ����(sh��)�ĵה�(sh��)).
������(����e����Ȼ����(sh��)�ĵה�(sh��)).
��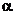 �����ֵ.
�����ֵ.
��: (��)����(sh��) �Ķ��x����
�Ķ��x����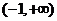 ��
��
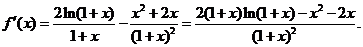
�O(sh��)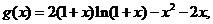 �t
�t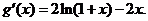
��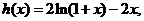 �t
�t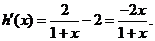
��(d��ng)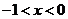 �r��
�r��
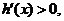 ��
��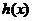 ��(-1��0)�Ϟ�������(sh��)��
��(-1��0)�Ϟ�������(sh��)��
��(d��ng)x��0�r��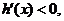
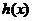 ��
��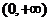 �Ϟ�p����(sh��).
�Ϟ�p����(sh��).
����h(x)��x=0̎ȡ�ØO��ֵ����h(0)=0,����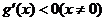 ��
��
����(sh��)g(x)��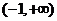 �Ϟ�p����(sh��).
�Ϟ�p����(sh��).
���Ǯ�(d��ng)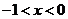 �r��
�r��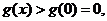
��(d��ng)x��0�r��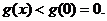
���ԣ���(d��ng)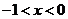 �r��
�r��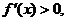
 ��(-1��0)�Ϟ�������(sh��).
��(-1��0)�Ϟ�������(sh��).
��(d��ng)x��0�r��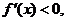
 ��
��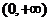 �Ϟ�p����(sh��).
�Ϟ�p����(sh��).
�ʺ���(sh��) �Ć��{(di��o)�f���^(q��)�g��(-1��0)�����{(di��o)�f�p�^(q��)�g��
���{(di��o)�f���^(q��)�g��(-1��0)�����{(di��o)�f�p�^(q��)�g��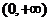 .
.
(��)����ʽ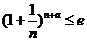 �ȃr�ڲ���ʽ
�ȃr�ڲ���ʽ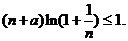 ��
��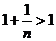 ֪��
֪��
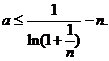 �� �O(sh��)
�� �O(sh��)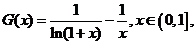 �t
�t
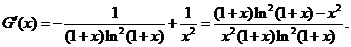
��(��)֪��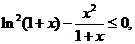 ��
��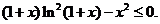
����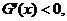
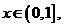 ����G(x)��
����G(x)��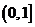 �Ϟ�p����(sh��).
�Ϟ�p����(sh��).
�ʺ���(sh��)G(x)��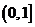 �ϵ���Сֵ��
�ϵ���Сֵ��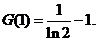
����a�����ֵ��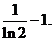
3.(2008ɽ�|��21)(��С�}�M��12��)
��֪����(sh��)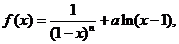 ����n��N*,a�鳣��(sh��).
����n��N*,a�鳣��(sh��).
(��)��(d��ng)n=2�r����(sh��)f(x)�ĘOֵ��
(��)��(d��ng)a=1�r���C�����������������(sh��)n,��(d��ng)x��2�r����f(x)��x-1.
(��)�⣺����֪�ú���(sh��)f(x)�Ķ��x��?y��n)�{x|x��1}��
������ ��(d��ng)n=2�r��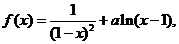
���� ���ԡ� 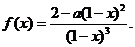
(1)��(d��ng)a��0�r����f(x)=0��
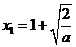 ��1��
��1��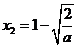 ��1��
��1��
�˕r�� f��(x)=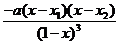 .
.
��(d��ng)x��(1��x1)�r��f��(x)��0,f(x)���{(di��o)�f�p��
��(d��ng)x��(x1+��)�r��f��(x)��0, f(x)���{(di��o)�f��.
(2)��(d��ng)a��0�r��f��(x)��0�����������f(x)�o�Oֵ.
�C��������n=2�r��
��(d��ng)a��0�r��f(x)��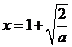 ̎ȡ�ØOСֵ���OСֵ��
̎ȡ�ØOСֵ���OСֵ��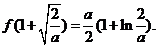
��(d��ng)a��0�r��f(x)�o�Oֵ.
(��)�C��һ����?y��n)?i>a=1,����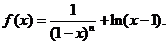
���������� ��(d��ng)n��ż��(sh��)�r��
��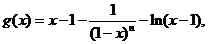
�t g��(x)=1+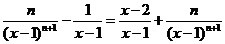 ��0(x��2).
��0(x��2).
���Ԯ�(d��ng)x��[2,+��]�r��g(x)���{(di��o)�f����
�֡� g(2)=0
���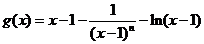 ��g(2)=0�������
��g(2)=0�������
�������� ����f(x)��x-1����.
��(d��ng)n���攵(sh��)�r��
�������� Ҫ�C ��x-1,����
��x-1,����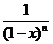 ��0������ֻ���Cln(x-1) ��x-1,
��0������ֻ���Cln(x-1) ��x-1,
�������� ��� h(x)=x-1-ln(x-1),
�������� �t���� h��(x)=1-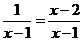 ��0(x��2),
��0(x��2),
�������� ���ԡ� ��(d��ng)x��[2��+��]�r��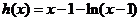 ���{(di��o)�f������h(2)=1��0��
���{(di��o)�f������h(2)=1��0��
������ ���Ԯ�(d��ng)x��2�r������h(x) ��0,��ln(x-1)��x-1���}����.
�C���������Y(ji��)Փ����.
�C��������(d��ng)a=1�r��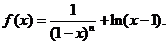
�������� ��(d��ng)x��2���r���������������(sh��)n������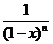 ��1��
��1��
�������� ��ֻ���C��1+ln(x-1) ��x-1.
�������� ��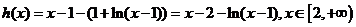
�������� �t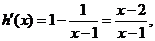
�������� ��(d��ng)x��2�r��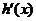 ��0����h(x)��
��0����h(x)��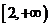 �φ��{(di��o)�f����
�φ��{(di��o)�f����
�������� ��ˡ���(d��ng)x��2�r��h(x)��h(2)=0����1+ln(x-1) ��x-1����.
�������� �ʡ���(d��ng)x��2�r����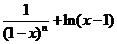 ��x-1.
��x-1.
�������� ��f(x)��x-1.
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com