
3.(2008年四川卷,數學文科理科,1)設集合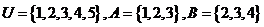 ,則
,則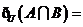 ( )
( )
(A)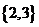 (B)
(B)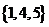 (C)
(C)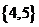 (D)
(D)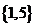
[解析]此題重點考察集合的交集,補集的運算;畫韋恩氏圖,數形結合;∵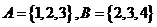 ∴
∴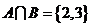 又∵
又∵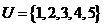
∴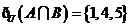
[答案]B
2.(2008年廣東卷,數學文科,1)第二十九屆夏季奧林匹克運動會將于2008年8月8日在北京舉行,若集合A={參加北京奧運會比賽的運動員},集合B={參加北京奧運會比賽的男運動員}。集合C={參加北京奧運會比賽的女運動員},則下列關系正確的是( )
A.A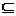 B
B.B
B
B.B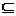 C
C.A∩B=C D.B∪C=A
C
C.A∩B=C D.B∪C=A
[解析]本題考查對集合概念的理解,易知B∪C=A,
[答案]D.
1.(2008年山東卷,數學文科理科,1)滿足M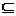 {a1,
a2, a3, a4},且M∩{a1 ,a2, a3}={ a1·a2}的集合M的個數是( )
{a1,
a2, a3, a4},且M∩{a1 ,a2, a3}={ a1·a2}的集合M的個數是( )
(A)1 (B)2 (C)3 (D)4
[解析]本小題主要考查集合子集的概念及交集運算。集合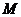 中必含有
中必含有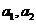 ,則
,則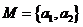 或
或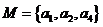
[答案]B
本節內容考試大綱的具體要求如下:
(1)集合的含義與表示
① 了解集合的含義、元素與集合的“屬于”關系.
② 能用自然語言、圖形語言、集合語言(列舉法或描述法)描述不同的具體問題.
(2)集合間的基本關系
① 理解集合之間包含與相等的含義,能識別給定集合的子集.
② 在具體情境中,了解全集與空集的含義.
(3)集合的基本運算
① 理解兩個集合的并集與交集的含義,會求兩個簡單集合的并集與交集.
② 理解在給定集合中一個子集的補集的含義,會求給定子集的補集.
③ 能使用韋恩(Venn)圖表達集合的關系及運算.
(二)考點預測題
1(遼寧省部分重點中學協作體2008年高考模擬).在△ABC中,角A,B,C的對邊為a,b,c,若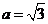 ,
,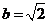 ,
,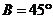 ,則角A=( )
,則角A=( )
A.30° B.30°或105° C.60° D.60°或120°
[解析]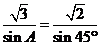 ,即
,即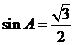 ,又
,又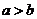 ,所以
,所以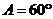 或
或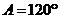 .
.
[答案]D.
2(2008年高考全國二17).在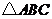 中,
中,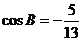 ,
,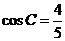 .
.
(Ⅰ)求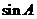 的值;
的值;
(Ⅱ)設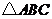 的面積
的面積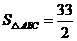 ,求
,求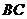 的長.
的長.
[解析](Ⅰ)由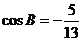 ,得
,得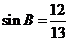 ,由
,由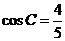 ,得
,得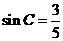 .
.
所以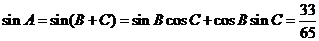 .
.
(Ⅱ)由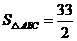 得
得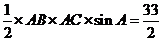 ,
,
由(Ⅰ)知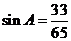 ,故
,故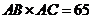 ,
,
又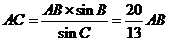 ,故
,故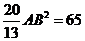 ,
,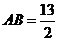 .
.
所以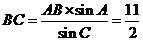 .
.
3(啟東市2009屆高三第一學期第一次調研考試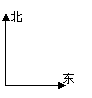 19)(2008年湖南理高考19).在一個特定時段內,以點E為中心的7海里以內海域被設為警戒水域.點E 正北55海里處有一個雷達觀測站A.某時刻測得一艘勻速直線行駛的船只位于點A北偏東
19)(2008年湖南理高考19).在一個特定時段內,以點E為中心的7海里以內海域被設為警戒水域.點E 正北55海里處有一個雷達觀測站A.某時刻測得一艘勻速直線行駛的船只位于點A北偏東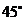 且與點A相距40
且與點A相距40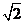 海里的位置B,經過40分鐘又測得該船已行駛到點A北偏東
海里的位置B,經過40分鐘又測得該船已行駛到點A北偏東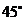 +
+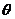 (其中sin
(其中sin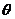 =
=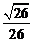 ,
,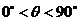 )且與點A相距10
)且與點A相距10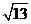 海里的位置C.
海里的位置C.
(1)求該船的行駛速度(單位:海里/小時);
(2)若該船不改變航行方向繼續行駛.判斷它是否會進入警戒水域,并說明理由.
[解析](1)如圖,AB=40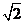 ,AC=10
,AC=10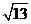 ,
,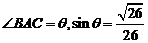 .
.
由于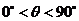 ,所以cos
,所以cos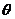 =
=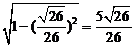 .
.
由余弦定理得BC=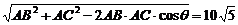
所以船的行駛速度為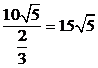 (海里/小時).
(海里/小時).
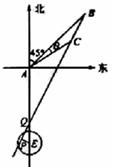
(2)解法一 如圖所示,以A為原點建立平面直角坐標系,
設點B、C的坐標分別是B(x1,y2), C(x1,y2),BC與x軸的交點為D.
 由題設有,x1=y1=
由題設有,x1=y1=
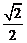 AB=40,
AB=40,
x2=ACcos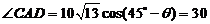 ,
,
y2=ACsin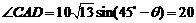 .
.
所以過點B、C的直線l的斜率k=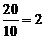 ,直線l的方程為y=2x-40.
,直線l的方程為y=2x-40.
又點E(0,-55)到直線l的距離d=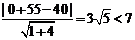 .
.
所以船會進入警戒水域.
解法二: 如圖所示,設直線AE與BC的延長線相交于點Q.
在△ABC中,由余弦定理得:
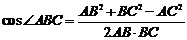 =
=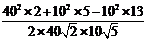 =
=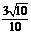 .
.
 從而
從而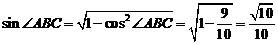 .
.
在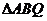 中,由正弦定理得,
中,由正弦定理得,
AQ=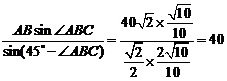 .
.
由于AE=55>40=AQ,所以點Q位于點A和點E之間,且QE=AE-AQ=15.
過點E作EP 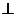 BC于點P,則EP為點E到直線BC的距離.
BC于點P,則EP為點E到直線BC的距離.
在Rt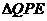 中,
中,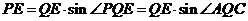
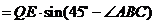 =
=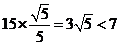 .
.
所以船會進入警戒水域.
(一)文字介紹
在解三角形中要求掌握正弦定理、余弦定理,并能解決一些簡單的三角形度量問題,能夠運用正弦定理、余弦定理等知識和方法解決一些與測量和幾何計算有關的問題.在具體解三角形時,要靈活運用已知條件,根據正、余弦定理,列出方程,進而求解,最后還要檢驗是否符合題意.
解三角形是高考必考內容,重點為正、余弦定理及三角形面積公式.可以以小題形式主要考查考題正、余弦定理及三角形面積公式;也可以是簡單的解答題,主要與三角函數的有關知識一起綜合考查;隨著課改的深入,聯系實際,注重數學在實際問題中的應用將是一個熱點,所以不排除考查解三角形與三角函數、函數等知識一起的綜合應用題,主要
考查學生的基本運算能力、應用意識和解決實際問題的能力.
1(福建2008年高考樣卷·文).△ABC的內角A、B、C所對的邊分別為a、b、c,若sinA=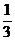 ,b=
,b=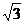 sinB,則a等于( )
A.
sinB,則a等于( )
A.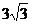 B.
B.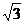 C.
C.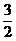 D.
D.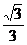
[解析]由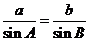 得
得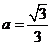 .
.
[答案]D.
2(山東省濟南市2009屆高三模考理10).在△ABC中,A=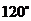 ,b=1,面積為
,b=1,面積為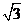 ,則
,則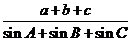 =( )
=( )
A.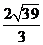 B.
B.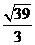 C.2
C.2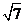 D.4
D.4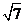
[解析]在△ABC中,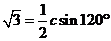 ,
,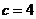 ;又
;又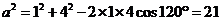 ,
,
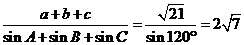 .
.
[答案]C.
3(2008-2009廈門質檢二).在△ABC中,tanA=,cosB=.若最長邊為1,則最短邊的長為( )
A. B. C. D.
[解析]由條件知A、B都是小于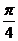 ,所以角C最大,又
,所以角C最大,又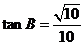 ,B最小,
,B最小,
由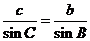 得,
得,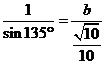 ,所以最短邊長為.
,所以最短邊長為.
[答案]D.
4(浙江省09年高考省教研室第一次抽樣測試數學試題(理)16).如圖,海平面上的甲船位于中心O的南偏西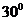 ,與O相距10海里的C處,現甲船以30海里/小時的速度沿直線CB去營救位于中心O正東方向20海里的B處的乙船,甲船需要
小時到達B處.
,與O相距10海里的C處,現甲船以30海里/小時的速度沿直線CB去營救位于中心O正東方向20海里的B處的乙船,甲船需要
小時到達B處.
[解析]由題意,對于CB的長度可用余弦定理求解,得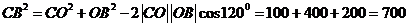 ,因此
,因此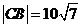 ,因此甲船需要的時間為
,因此甲船需要的時間為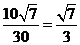 (小時).
(小時).
[答案]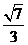 .
.
5 (江蘇省南京市2009屆高三第一次質量檢測數學試題11) .在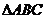 中,角
中,角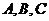 所對的邊分別為
所對的邊分別為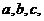
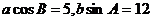 ,則
,則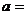 .
.
[解析]由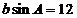 及正弦定理得:
及正弦定理得: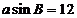 ,又
,又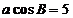 ,
,
兩式平方相加得: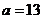 .
.
[答案]13.
6(浙江2008學年第一學期十校高三期末聯考數學試題(理))
.在△ABC中,角A,B,C所對的邊分別是a,b,c,若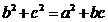 ,且
,且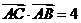 ,則△ABC的面積等于
.
,則△ABC的面積等于
.
[解析]由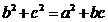 及余弦定理得:
及余弦定理得: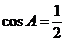 ,由
,由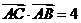 得
得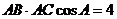 ,所以
,所以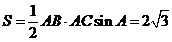 .
.
[答案]2 .
7(和平區2008年高考數學(理)三模13). 在△ABC中,設角A、B、C的對邊分別為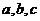 ,且
,且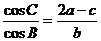 ,則角B= 度.
,則角B= 度.
[解析]由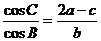 及正弦定理得:
及正弦定理得: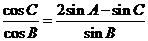 ,
,
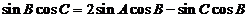 ,所以
,所以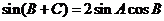 ,所以
,所以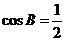 ,又
,又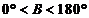 ,
,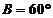 .
.
[答案]60.
 8(廣東省四校聯考2009屆高三上學期期末考試數學理15).如圖在
8(廣東省四校聯考2009屆高三上學期期末考試數學理15).如圖在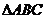 中,
中,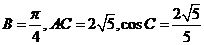
(1)求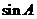 ; (2) 記
; (2) 記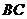 的中點為
的中點為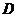 , 求中線
, 求中線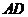 的長.
的長.
 [解析](1)由
[解析](1)由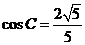 ,
, 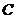 是三角形內角,
是三角形內角,
得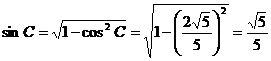
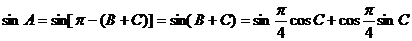
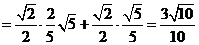
(2) 在△ABC中,由正弦定理,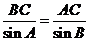 ,
,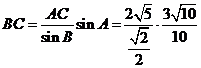
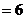
Þ CD = BC = 3 , 又在△ADC中, AC=2, cosC = ,
由余弦定理得, 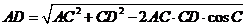
=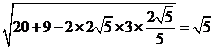
9(2009年濱海新區五所重點學校聯考理17).在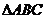 中,
中,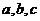 分別是角
分別是角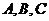 的對邊,
的對邊,
且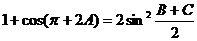 .
.
(Ⅰ)求角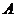 的大小;
的大小;
(Ⅱ)當a=6時,求其面積的最大值,并判斷此時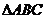 的形狀.
的形狀.
[解析](Ⅰ)由已知得: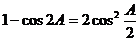 ,
,
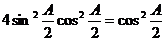 ,
,
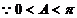 ,∴
,∴ 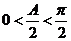
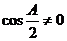 ,
,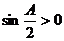
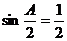 ,∴
,∴ 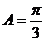 .
.
(Ⅱ) 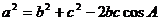 ,∴
,∴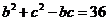 ,
,
∴
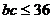 .
.
故三角形的面積 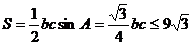 .
.
當且僅當b=c時等號成立;又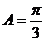 ,故此時
,故此時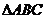 為等邊三角形.
為等邊三角形.
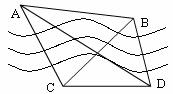 10(漢沽一中2009屆高三月考文18).如圖,隔河看兩目標A、B,但不能到達,在岸邊選取相距
10(漢沽一中2009屆高三月考文18).如圖,隔河看兩目標A、B,但不能到達,在岸邊選取相距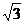 km的C、D兩點,并測得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面內),求兩目標A、B之間的距離.
km的C、D兩點,并測得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面內),求兩目標A、B之間的距離.
[解析]在△ACD中,∠ADC=30°,∠ACD=120°,∴∠CAD=30°,
∴AC=CD=3.
在△BDC中,∠CBD=180°-(45°+75°)=60°,
由正弦定理,得BC=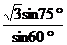 =
=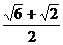 ,
,
由余弦定理,得AB2=AC2+BC2-2AC·BC·cos∠BCA
=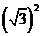 +
+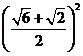 -2
-2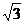 ×
×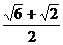 cos75°=5.∴AB=
cos75°=5.∴AB=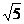 .
.
∴兩目標A、B之間的距離為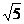 km.
km.
1(2008年高考山東卷15).已知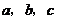 為
為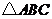 的三個內角
的三個內角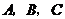 的對邊,
的對邊,
向量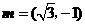 ,
,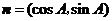 .若
.若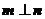 ,且
,且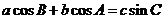 ,則角
,則角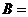 .
.
[解析]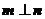
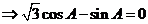
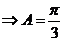 ,
,
由正弦定理得: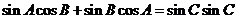 ,
,
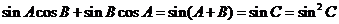
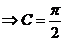
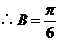 .
.
[答案]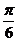 .
.
 2(2007年天津文17).在
2(2007年天津文17).在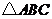 中,已知
中,已知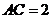 ,
,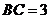 ,
,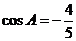 .
.
(Ⅰ)求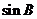 的值;
的值;
(Ⅱ)求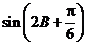 的值.
的值.
[解析](Ⅰ)在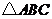 中,
中,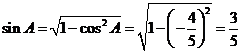 ,由正弦定理,
,由正弦定理,
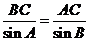 .
所以
.
所以 .
.
(Ⅱ)解:因為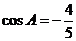 ,所以角
,所以角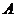 為鈍角,從而角
為鈍角,從而角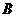 為銳角,于是
為銳角,于是
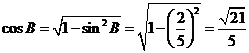 ,
,
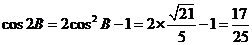 ,
,
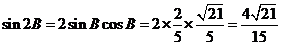 .
.
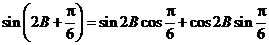
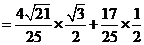
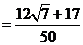 .
.
3(2008年高考重慶卷17).設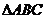 的內角A,B,C的對邊分別為
的內角A,B,C的對邊分別為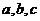 ,且
,且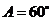 ,
,
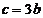 ,求:
,求:
(Ⅰ)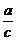 的值;
的值;
(Ⅱ)cotB +cot C的值.
[解析](Ⅰ)由余弦定理得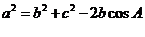 =
=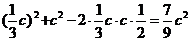
故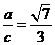 .
.
(Ⅱ)解法一: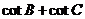 =
=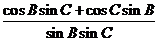
=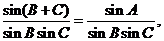
由正弦定理和(Ⅰ)的結論得
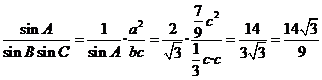 ,
,
故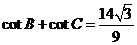 .
.
解法二:由余弦定理及(Ⅰ)的結論有
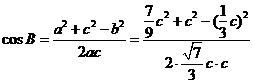 =
=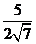
故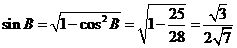 .
.
同理可得

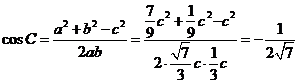
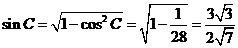 .
.
從而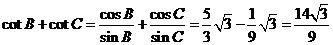 .
.
4(2008年高考遼寧卷17).在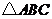 中,內角
中,內角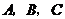 對邊的邊長分別是
對邊的邊長分別是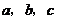 ,已知
,已知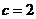 ,
,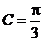 .
.
(Ⅰ)若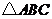 的面積等于
的面積等于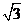 ,求
,求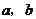 ;
;
(Ⅱ)若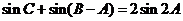 ,求
,求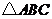 的面積.
的面積.
[解析](Ⅰ)由余弦定理及已知條件得,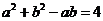 ,
,
又因為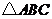 的面積等于
的面積等于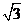 ,所以
,所以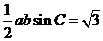 ,得
,得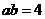 .
.
聯立方程組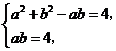 解得
解得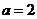 ,
,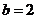 .
.
(Ⅱ)由題意得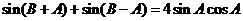 ,
,
即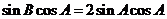 ,
,
當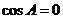 時,
時,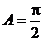 ,
,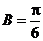 ,
,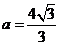 ,
,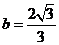 ,
,
當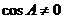 時,得
時,得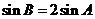 ,由正弦定理得
,由正弦定理得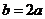 ,
,
聯立方程組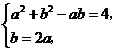 解得
解得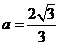 ,
,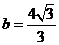 .
.
所以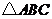 的面積
的面積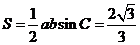 .
.
5(2008年高考全國一17).設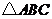 的內角
的內角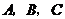 所對的邊長分別為
所對的邊長分別為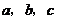 ,且
,且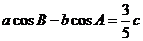 .
.
(Ⅰ)求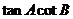 的值;
的值;
(Ⅱ)求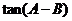 的最大值.
的最大值.
[解析](Ⅰ)在 中,由正弦定理及
中,由正弦定理及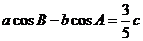
可得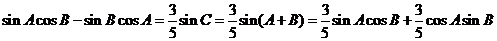
即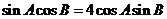 ,則
,則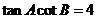 ;
;
(Ⅱ)由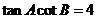 得
得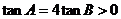
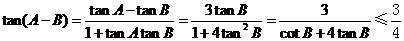
當且僅當 時,等號成立,
時,等號成立,
故當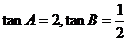 時,
時,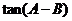 的最大值為
的最大值為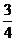 .
.
2.正弦定理和余弦定理的應用
能夠運用正弦定理、余弦定理等知識和方法解決一些與測量和幾何計算有關的實際問題.
解三角形是高考必考內容,重點為正余弦定理及三角形面積公式,考題靈活多樣,近幾年經常以解答題的形式來考查,若以解決實際問題為背景的試題,有一定的難度.
1.正弦定理和余弦定理
掌握正弦定理、余弦定理,并能解決一些簡單的三角形度量問題.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com