
題目列表(包括答案和解析)
在△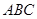 中,
中,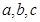 分別為內角
分別為內角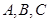 的對邊,且
的對邊,且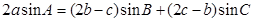 .
.
(1)求角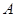 的大小;
的大小;
(2)若 +
+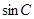 =
=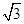 ,試判斷△
,試判斷△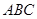 的形狀.
的形狀.
【解析】本試題主要考查了解三角形中正弦定理和余弦定理的運用。求解變和角,并定形的問題。
觀察下面兩個推理過程及結論:
若銳角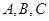 滿足
滿足 ,以角
,以角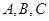 分別為內角構造一個三角形,依據正弦定理和余弦定理可得到等式:
分別為內角構造一個三角形,依據正弦定理和余弦定理可得到等式: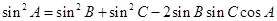 ,
,
若銳角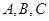 滿足
滿足 ,則
,則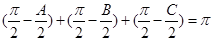 ,以角
,以角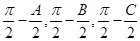 分別為內角構造一個三角形,依據正弦定理和余弦定理可以得到的等式:
分別為內角構造一個三角形,依據正弦定理和余弦定理可以得到的等式: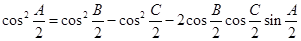 .
.
則:若銳角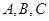 滿足
滿足 ,類比上面推理方法,可以得到的一個等式是______________.
,類比上面推理方法,可以得到的一個等式是______________.
觀察下面兩個推理過程及結論:
(1) 若銳角A, B, C滿足A+B+C=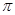 , 以角A, B, C分別為內角構造一個三角形, 依據正弦定理和余弦定理可得到等式:
, 以角A, B, C分別為內角構造一個三角形, 依據正弦定理和余弦定理可得到等式: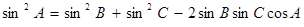
(2) 若銳角A, B, C滿足A+B+C=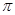 , 則
, 則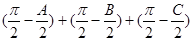 =
=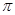 , 以
, 以
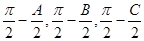 分別為內角構造一個三角形, 依據正弦定理和余弦定理可以
分別為內角構造一個三角形, 依據正弦定理和余弦定理可以
得到的等式: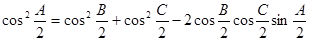 則:若銳角A, B, C滿
則:若銳角A, B, C滿
足A+B+C=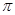 , 類比上面推理方法, 可以得到一個等式是 .
, 類比上面推理方法, 可以得到一個等式是 .
觀察下面兩個推理過程及結論:
若銳角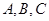 滿足
滿足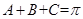 ,以角
,以角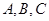 分別為內角構造一個三角形,依據正弦定理和余弦定理可得到等式:
分別為內角構造一個三角形,依據正弦定理和余弦定理可得到等式: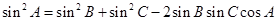 ,
,
若銳角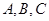 滿足
滿足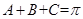 ,則
,則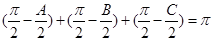 ,以角
,以角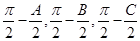 分別為內角構造一個三角形,依據正弦定理和余弦定理可以得到的等式:
分別為內角構造一個三角形,依據正弦定理和余弦定理可以得到的等式: .
.
則:若銳角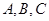 滿足
滿足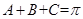 ,類比上面推理方法,可以得到的一個等式是______________.
,類比上面推理方法,可以得到的一個等式是______________.
如圖,A,B是海面上位于東西方向相距 海里的兩個觀測點,現位于A點北偏東45°,B點北偏西60°的D點有一艘輪船發出求救信號,位于B點南偏西60°且與B點相距
海里的兩個觀測點,現位于A點北偏東45°,B點北偏西60°的D點有一艘輪船發出求救信號,位于B點南偏西60°且與B點相距 海里的C點的救援船立即即前往營救,其航行速度為30海里/小時,該救援船到達D點需要多長時間?
海里的C點的救援船立即即前往營救,其航行速度為30海里/小時,該救援船到達D點需要多長時間?

【解析】本試題考查了利用正弦定理和余弦定理求解三角形的實際運用。并考查了分析問題和解決問題的能力。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com