在△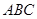
中，
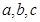分別為內角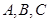
的對邊，且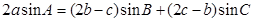
．
(1)求角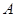
的大小；
(2)若
＋
＝
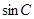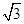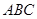，試判斷△的形狀．
【解析】本試題主要考查了解三角形中正弦定理和余弦定理的運用。求解變和角，并定形的問題。
解：(1)由2asin A＝(2b－c)sin B＋(2c－b)sin C，
得2a2＝(2b－c)b＋(2c－b)c，即bc＝b2＋c2－a2，
∴cos A＝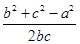
＝
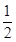，∴A＝60°.
5分
(2)∵A＋B＋C＝180°，∴B＋C＝180°－60°＝120°.
由sin B＋sin C＝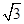
，得sin B＋sin(120°－B)＝，
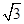∴sin B＋sin
120°cos B－cos 120°sin B＝.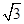
∴
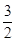sin B＋
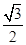cos B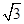＝，即sin(B＋30°)＝1. -----------9分
∵0°<B<120°，∴30°<B＋30°<150°.
∴B＋30°＝90°，B＝60°. ∴A＝B＝C＝60°，△ABC為正三角形．
科目：高中數學 來源：2012-2013學年河北省唐山市高三第一次月考文科數學試卷（解析版） 題型：解答題
（10分）在△ABC中，
分別為內角A.B.C所對的邊，且滿足
（1）求角A的大小
（2）現給出三個條件：①
②
③
試從中選出兩個可以確定△ABC的條件寫出你的選擇，并以此為依據求△ABC的面積（只需寫出一個選定方案即可，選多種方案以第一種方案記分）
查看答案和解析>>
科目：高中數學 來源：2011年廣東省揭陽市高二上學期期末檢測數學理卷 題型：解答題
若（本題12分）在△ABC中，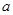
, 
, 
分別為內角A, B, C的對邊，且
（Ⅰ）求A的大小； （Ⅱ）求
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
中，
分別為內角
的對邊，已知
，則
（ ）
B. 
C.
D.
中，
分別為內角
的對邊，若
，且
，則角B= ．
中，
分別為內角
的對邊，若
，則
的值為（ ）
B．
C．
D．