
1.平面向量的實際背景及基本概念
(1)了解向量的實際背景.
(2)理解平面向量的概念,理解兩個向量相等的含義.
(3)理解向量的幾何表示.
4、已知不等式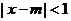 成立的一個充分非必要條件是
成立的一個充分非必要條件是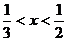 ,則
,則
實數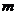 的取值范圍是( )
的取值范圍是( )
A.  ; B.
; B.  ; C.
; C.  ; D.
; D. 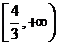 .
.
3、集合P=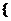 1,3,5,7,9,┅,2
1,3,5,7,9,┅,2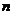 -1,┅
-1,┅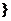
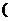
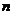 ∈N
∈N
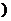 ,若
,若 ∈P,
∈P,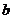 ∈P時,
∈P時,
 @
@ 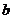 ∈P,則運算 可能是( D )
∈P,則運算 可能是( D )
(A)加法; (B)除法; (C)減法; (D)乘法.
2、已知命題P:. ,
,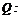 不等式
不等式 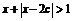 的解集為
的解集為 .如果
.如果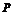 和
和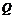 有且僅有一個正確,則
有且僅有一個正確,則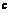 的取值范圍是
.
的取值范圍是
.
[解析]若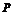 和
和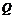 都正確,則由
都正確,則由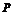 ,有
,有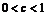 .由
.由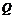 ,有
,有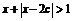 的解集為
的解集為 .
.
用函數認識不等式,只需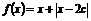 的最小值
的最小值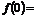 2
2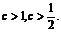 此時
此時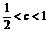 .
.
若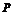 和
和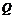 都不正確,則由
都不正確,則由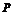 ,有
,有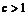 .由
.由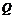 ,有
,有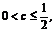 其交集為空集,此時
其交集為空集,此時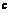 不存在.
不存在.
由題設知,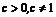 ,用補集思想,所求
,用補集思想,所求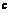 的取值范圍為
的取值范圍為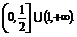 .
.
本章三個知識點,高考一般結合其它章節知識命制兩個小題:(1)集合概念運算為核心;(2)以充分必要條件為形式。
1、設函數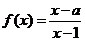 ,集合M=
,集合M=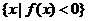 ,P=
,P= ,若M
,若M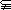 P,則實數a的取值范圍是集合M,則M=
.
P,則實數a的取值范圍是集合M,則M=
.
解析:設函數 ,
集合
,
集合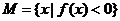 .
.
若a>1時,M={x| 1<x<a};
若a<1時,M={x| a<x<1};
a=1時,M=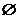 .
.
 ,∴
,∴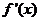 =
=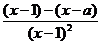 >0.
>0.
∴ a>1時,P=R,a<1時,P=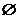 ;已知
;已知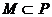 ,所以 M=(1,+∞).
,所以 M=(1,+∞).
7、定義“逆運算※”,對于 中的任意兩個元素
中的任意兩個元素
 ,
,
規定: ※
※
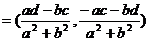 解釋合理性(如6)
解釋合理性(如6)
評析:本題創設新情景,綜合考查了集合運算,方程、函數、數的運算性質等知識。又考查了抽象運算及思考,創新能力等。
6、方程 ⊙
⊙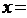
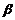 當
當 時有解,并求出解
時有解,并求出解 ………………5分
………………5分
5、方程 ⊙
⊙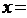
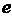 當
當 時有解,并求出解
時有解,并求出解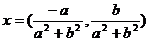 …………………4分
…………………4分
4、證明消去律成立: ⊙
⊙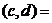
 ⊙
⊙
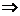
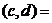
 ………………………3分
………………………3分
3、定義“加法”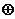 :
:
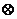
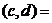
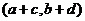 ,
,
并解釋合理性(驗證
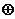
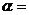
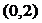 ⊙
⊙ )…………………………………………………………2分
)…………………………………………………………2分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com