
8.設奇函數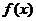 在
在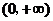 上為增函數,且
上為增函數,且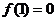 ,則不等式
,則不等式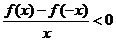 的解集為( )
的解集為( )
A.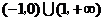 B.
B.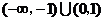
C.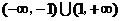 D.
D.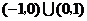
7.已知函數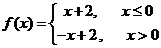 ,則不等式
,則不等式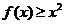 的解集是( )
的解集是( )
(A)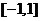 (B)
(B)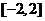 (C)
(C)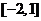 (D)
(D)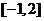
6.若點P(2,0)到雙曲線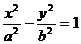 的一條漸線的距離為
的一條漸線的距離為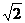 ,則雙曲線的離心率為( )
,則雙曲線的離心率為( )
(A)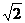 (B)
(B)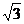 (C)
(C)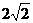 (D)
(D)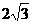
5.復數 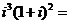 ( )
( )
A.2 B.-2 C. 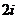 D.
D. 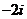
4.已知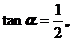 ,則
,則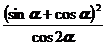 = ( )
= ( )
(A)2 (B)-2 (C)3 (D)-3
3.函數f(x)=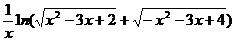 的定義域為
的定義域為
A.(- ∞,-4)[∪2,+ ∞] B.(-4,0) ∪(0,1)
C. [-4,0]∪(0,1)] D. [-4,0∪(0,1)
2.用與球心距離為1的平面去截球,所得的截面面積為π,則球的休積為
A.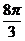 B.
B. 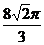 C.
C.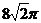 D.
D. 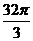
1.若非空集合A,B,C滿足A∪B=C,且B不是A的子集,則
A.“x∈C”是“x∈A”的充分條件但不是必要條件
B. “x∈C”是“x∈A”的必要條件但不是充分條件
C. “x∈C”是“x∈A”的充分條件
D. “x∈C”是“x∈A”的充分條件也不是“x∈A”必要條件
21.(本題滿分14分)
已知數列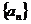 中,
中,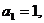 且點
且點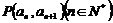 在直線
在直線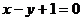 上.
上.
(1)求數列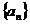 的通項公式;
的通項公式;
(2)若函數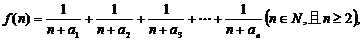 求函數
求函數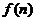 的最小值;
的最小值;
(3)設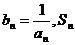 表示數列
表示數列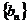 的前項和.試問:是否存在關于
的前項和.試問:是否存在關于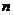 的整式
的整式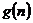 ,使得
,使得
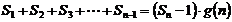 對于一切不小于2的自然數
對于一切不小于2的自然數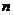 恒成立?
若存在,寫出
恒成立?
若存在,寫出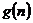 的解析式,并加以證明;若不存在,試說明理由.(東莞市2009屆高三模擬試題(二))
的解析式,并加以證明;若不存在,試說明理由.(東莞市2009屆高三模擬試題(二))
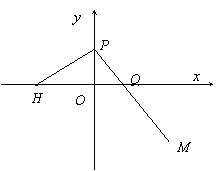
20、(14分)已知點H(-3,0),點P在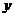 軸上,點Q在
軸上,點Q在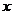 軸的正半軸上,點M在直線PQ上,且滿足
軸的正半軸上,點M在直線PQ上,且滿足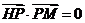 ,
, 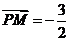
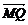 .
.
(Ⅰ)當點P在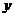 軸上移動時,求點M的軌跡C;
軸上移動時,求點M的軌跡C;
(Ⅱ)過定點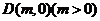 作直線
作直線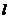 交軌跡C于A、B兩點,E是D點關于坐標原點O的對稱點,求證:
交軌跡C于A、B兩點,E是D點關于坐標原點O的對稱點,求證: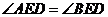 ;
;
 (Ⅲ)在(Ⅱ)中,是否存在垂直于
(Ⅲ)在(Ⅱ)中,是否存在垂直于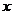 軸的直線
軸的直線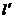 被以AD為直徑的圓截得的弦長恒為定值?若存在求出
被以AD為直徑的圓截得的弦長恒為定值?若存在求出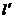 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com