
20.(14分)已知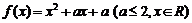 ,
,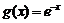 ,
,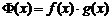 .
.
(1)當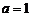 時,求
時,求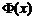 的單調區間;
的單調區間;
(2)求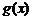 在點
在點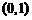 處的切線與直線
處的切線與直線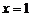 及曲線
及曲線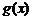 所圍成的封閉圖形的面積;
所圍成的封閉圖形的面積;
(3)是否存在實數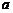 ,使
,使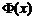 的極大值為3?若存在,求出
的極大值為3?若存在,求出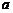 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
18.(14分) 已知圓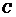 方程為:
方程為: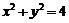 .
.
(1)直線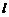 過點
過點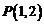 ,且與圓
,且與圓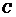 交于
交于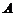 、
、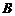 兩點,若
兩點,若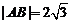 ,求直線
,求直線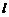 的方程;
的方程;
(2)過圓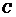 上一動點
上一動點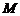 作平行于
作平行于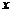 軸的直線
軸的直線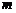 ,設
,設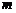 與
與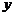 軸的交點為
軸的交點為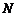 ,若向量
,若向量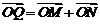 ,求動點
,求動點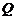 的軌跡方程,并說明此軌跡是什么曲線.
的軌跡方程,并說明此軌跡是什么曲線.
 19.(14分)如圖,在長方體
19.(14分)如圖,在長方體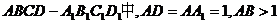 ,點E在棱AB上移動,小螞蟻從點A沿長方體的表面爬到點C1,所爬的最短路程為
,點E在棱AB上移動,小螞蟻從點A沿長方體的表面爬到點C1,所爬的最短路程為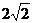 .
.
(1)求證:D1E⊥A1D;
(2)求AB的長度;
(3)在線段AB上是否存在點E,使得二面角
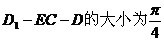 。若存在,確定
。若存在,確定
點E的位置;若不存在,請說明理由.
17. (12分)某公司有10萬元資金用于投資,如果投資甲項目,根據市場分析知道:一年后可能獲利10﹪,可能損失10﹪,可能不賠不賺,這三種情況發生的概率分別為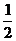 ,
,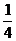 ,
,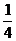 ;如果投資乙項目,一年后可能獲利20﹪,也可能損失20﹪,這兩種情況發生的概率分別為
;如果投資乙項目,一年后可能獲利20﹪,也可能損失20﹪,這兩種情況發生的概率分別為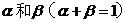 .
.
(1)如果把10萬元投資甲項目,用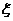 表示投資收益(收益=回收資金-投資資金),求
表示投資收益(收益=回收資金-投資資金),求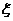 的概率分布及
的概率分布及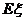 ;
;
(2)若把10萬元投資投資乙項目的平均收益不低于投資甲項目的平均收益,求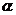 的取值范圍.
的取值范圍.
16. (12分)設函數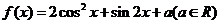 .
.
(1)求函數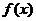 的最小正周期和單調遞增區間;
的最小正周期和單調遞增區間;
(2)當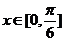 時,
時,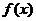 的最大值為2,求
的最大值為2,求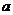 的值,并求出
的值,并求出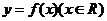 的對稱軸方程.
的對稱軸方程.
(二)選做題(13--15題,考生只能從中選作2題)
13.(坐標系與參數方程選做題) (坐標系與參數方程選做題)兩直線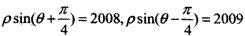 的位置關系是______(判斷垂直或平行或斜交)
的位置關系是______(判斷垂直或平行或斜交)
14. (不等式選講選做題)
不等式
(不等式選講選做題)
不等式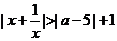 對于一非零實數x均成立,則實數a的取值范圍是_________
對于一非零實數x均成立,則實數a的取值范圍是_________
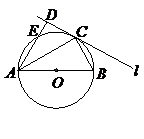
15.(幾何證明選講選做題) 如圖所示,圓O的直徑AB=6,C為圓周上一點,BC=3,過C作圓的切線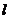 ,則點A到直線
,則點A到直線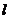 的距離AD為 .
的距離AD為 .
(一)必做題(9--12題)
9.在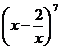 的展開式中,
的展開式中,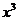 的系數是
.(用數字作答)
的系數是
.(用數字作答)
10. 一個均勻小正方體的六個面中,三個面上標以數0,兩個面上標以數1,一個面上標以數2,將這個小正方體拋擲2次,則向上的數之積為0的概率
.
一個均勻小正方體的六個面中,三個面上標以數0,兩個面上標以數1,一個面上標以數2,將這個小正方體拋擲2次,則向上的數之積為0的概率
.
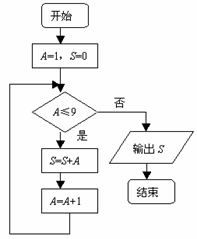
11.如圖,該程序運行后輸出的結果為 .
12.已知點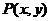 滿足條件
滿足條件
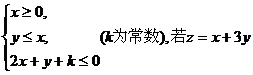 的最大值為8,
的最大值為8,
則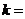 .
.
8.已知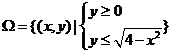 ,直線
,直線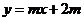 和曲線
和曲線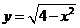 有兩個不同的交點,它們圍成的平面區域為
有兩個不同的交點,它們圍成的平面區域為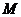 ,向區域
,向區域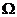 上隨機投一點A,點A落在區域
上隨機投一點A,點A落在區域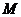 內的概率為
內的概率為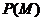 ,若
,若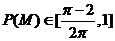 ,則實數
,則實數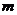 的取值范圍為
的取值范圍為
A.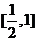 B.
B.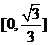 C.
C.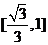 D.
D. 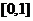
7.兩個正數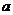 、
、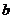 的等差中項是
的等差中項是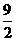 ,一個等比中項是
,一個等比中項是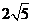 ,且
,且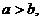 則雙曲線
則雙曲線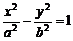 的離心率為
的離心率為
A.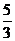 B.
B.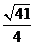 C.
C.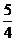 D.
D.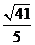
6.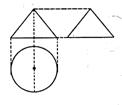 如右圖,一個空間幾何體的主視圖和左視圖都是邊長為1的正三角形,俯視圖是一個圓,那么幾何體的側面積為
如右圖,一個空間幾何體的主視圖和左視圖都是邊長為1的正三角形,俯視圖是一個圓,那么幾何體的側面積為
A. 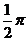 B.
B. 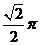
C. 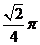 D.
D.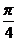
5.已知函數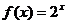 的反函數
的反函數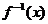 滿足
滿足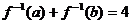 ,則
,則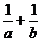 的最小值為
的最小值為
A.1 B.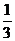 C.
C.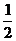 D.
D.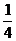
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com