
(三)高頻考點及考題類型
1、直線以傾斜角、斜率、夾角、距離、平行與垂直、線性規劃(老)等有關的問題,其中要重視“對稱問題”及”線性規劃問題”的解答。
2、與圓位置有關的問題,一是研究方程組;二是充分利用平面幾何知識。重在后者。
3、求曲線的方程或軌跡問題,涉及圓錐曲線的定義和幾何性質(如求離心率的問題)
4、直線與圓錐曲線的位置關系問題,如參數的變量取值范圍、最值;幾何參量的求值問題。
5、以圓錐曲線為載體在知識網絡的交匯點設計問題,其目的是加強聯系注重應用,考查學生的應變能力以及分析問題和解決問題的能力。
(一)基本知識網絡
 (二)基本知識點(定義公式)
(二)基本知識點(定義公式)
1、 直線
(1)兩點P1(x1,y1)、P2(x2,y2)的距離公式: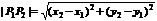 .
.
若直線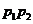 的斜率為k,則
的斜率為k,則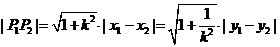 .
.
(老教材)定比分點坐標分式。若點P(x,y)分有向線段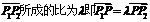 ,其中P1(x1,y1),P2(x2,y2).則
,其中P1(x1,y1),P2(x2,y2).則
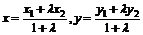
特例,中點坐標公式;重要結論,三角形重心坐標公式。
(2) 直線的傾斜角(0°≤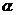 <180°)、斜率:
<180°)、斜率: 過兩點
過兩點 .
. 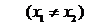
當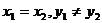 (即直線和x軸垂直)時,直線的傾斜角
(即直線和x軸垂直)時,直線的傾斜角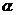 =
=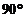 ,沒有斜率
,沒有斜率
(3)直線方程的幾種形式:
|
直線名稱 |
已知條件 |
直線方程 |
使用范圍 |
|
點斜式 |
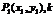 |
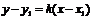 |
k存在 |
|
斜截式 |
k,b |
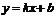 |
k存在 |
|
兩點式 |
(x1,y1)、(x2,y2) |
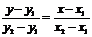 |
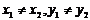 |
|
截距式 |
a,b |
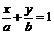 |
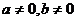 |
|
一般式 |
|
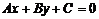 |
A、B不全為0 |
|
參數式 |
傾斜角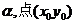 |
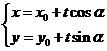 |
t為參數 |
(4)兩條直線的位置關系
①若兩條直線的方程分別為 l1: y=k1x+b1; l2: y=k2x+b2.則
l1|| l2⇔k1=k2,且b1≠b2; l1⊥l2⇔k1•k2= -1 ;
當1+k1k2≠0時,若q為l1到l2的角,則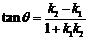 , 若α為l1和l2的夾角則
, 若α為l1和l2的夾角則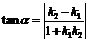 ,
,
②如果直線l1、l2的方程分別為l1:A1x+B1y+C1=0, l2: A2x+B2y+C2=0 則l1與l2
相交的充要條件: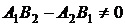 ;交點坐標:
;交點坐標: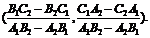
. 平行的充要條件:l1|| l2⇔A1B2-A2B1=0,(B1C2-B2C1)2+(C1A2-C2A1)2≠0.
垂直的充要條件:l1⊥ l2⇔A1A2+B1B2=0.
重合的充要條件:l1與l2重合⇔A1B2-A2B1=B1C2-B2C1=C1A2-C2A1=0 (或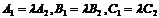 ).
).
若 A1A2+B1B2≠0,直線l1到直線l2的角是θ,則有tanθ=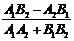
(5)直線系方程
①與直線:Ax+By+C= 0平行的直線系方程是:Ax+By+m=0.( m∊R, C≠m).
② 與直線:Ax+By+C= 0垂直的直線系方程是:Bx-Ay+m=0.( m∊R)
③ 過定點(x1,y1)的直線系方程是: A(x-x1)+B(y-y1)=0 (A,B不全為0)
④ 過直線l1、l2交點的直線系方程:(A1x+B1y+C1)+λ( A2x+B2y+C2)=0 (λ∊R) 注:該直線系不含l2.
(5)距離
①點P(xo,yo)到直線l:Ax+By+C=
0的距離
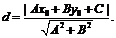
②兩平行線l1:Ax+By+c1=0, l2:Ax+By+c2=0間的距離公式:d=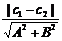
2、圓
(1) 圓的定義:平面上到一定點的距離等于定長的點的軌跡。
(2) 圓的方程
① 圓的標準方程:(x-a)2+(y-b)2=r2
②一般方程:x2+y2+Dx+Ey+F=0,(D2+E2-4F>0) 圓心坐標:(-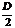 ,-
,-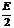 ) 半徑r=
) 半徑r=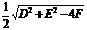

③以(x1,y1),(x2,y2)為直徑兩端的圓的方程:(x-x1)(x-x2)+(y-y1)(y-y2)=0
④圓的參數方程: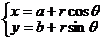 (
(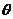 為參數)
為參數)
(3) 點與圓的位置關系
設圓C∶(x-a)2+(y-b)2=r2,點M(x0,y0)到圓心的距離為d,則有:
幾何表示(1)d>r 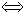 點M在圓外; (2)d=r
點M在圓外; (2)d=r 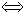 點M在圓上;
(3)d<r
點M在圓上;
(3)d<r 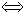 點M在圓內.
點M在圓內.
代數表示(x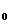 -a)2+(y
-a)2+(y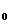 -b)2>r2
-b)2>r2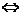 點M在圓外;(x
點M在圓外;(x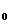 -a)2+(y
-a)2+(y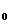 -b)2=r2
-b)2=r2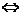 點M在圓上;(x
點M在圓上;(x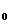 -a)2+(y
-a)2+(y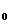 -b)2<r2
-b)2<r2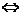 點M在圓內;
點M在圓內;
(4)直線與圓的位置關系
設圓C:(x-a)2+(y-b)2=r2, 直線l的方程為Ax+By+C=0.1圓心(a,b)到l的距離為d;
2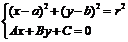 消去y得關于x的一元二次方程判別式為△,則有:
消去y得關于x的一元二次方程判別式為△,則有:
|
位置關系 |
公共點個數 |
數量關系 |
|
|
相離 |
0 |
d>r |
⊿< 0 |
|
相切 |
1 |
d=r |
⊿ = 0 |
|
相交 |
2 |
d<r |
⊿> 0 |
(5) 圓與圓的位置關系
設圓C1:(x-a)2+(y-b)2=r12和圓C2:(x-m)2+(y-n)2=r22(r1≥r2),且設兩圓圓心距為d,則有:
|
位置關系 |
相離 |
外切 |
相交 |
內切 |
內含 |
|
數量關系 |
d> r1+r2 |
d=r1+r2 |
r1-r2<d<r1+r2 |
d=r1-r2 |
d<r1-r2(d=0:兩圓同心) |
(6)幾個常用結論和方法
①弦長的求解:弦心距d、圓半徑r、弦長l,則: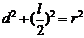 (根據垂弦定理和勾股定理)
(根據垂弦定理和勾股定理)
②圓的切線方程的求法
過圓上的點的圓的切線方程
..圓x2+y2=r2,圓上一點為(x0,y0),則此點的切線方程為x0x+y0y=r2(課本命題).
..圓(x-a)2+(y-b)2=r2,圓上一點為(x0,y0),則過此點的切線方程為(x0-a)(x-a)+(y0-b)(y-b)=r2(課本命題的推廣).
..以(x0,y0)為切點的圓x2+y2+Dx+Ey+F=0的切線方程:分別以xox,yoy,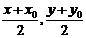 替換圓方程中的x2,y2,x,y.
替換圓方程中的x2,y2,x,y.
過圓外一點M(xo,yo),作圓(x-a)2+(y-b)2=r2的切線,可設切線方程為點斜式:
y-yo=k(x-xo),利用圓心到直線的距離等于半徑或與圓的方程聯立用判別式法求k。
注意: 由圓外一點向圓引切線,應當有兩條切線。但,可能只算出一個 k值,那么,另一條斜率不存在,即過(x0,y0)垂直于x軸的直線x=x0.
③兩圓相交時的公共弦方程、兩圓外切時的內公切線、兩圓內切時的外公切線:兩圓方程作差,消去二次項所得的直線方程即為所求。
3圓錐曲線
(1)橢圓、雙曲線、拋物線的標準方程與幾何性質(見后表)
(2)橢圓、雙曲線、拋物線的標準方程的其他形式及相應性質.
(3)等軸雙曲線
(4)共軛雙曲線
(5)方程y2=ax與x2=ay的焦點坐標及準線方程.
(6)共漸近線的雙曲線系方程.
(7)點、直線與圓錐曲線的位置關系
橢圓、雙曲線、拋物線的標準方程與幾何性質
|
|
橢圓 |
雙曲線 |
拋物線 |
|
|
定義 |
1.到兩定點F1,F2的距離之和為定值2a(2a>|F1F2|)的點的軌跡 |
1.到兩定點F1,F2的距離之差的絕對值為定值2a(0<2a<|F1F2|)的點的軌跡 |
|
|
|
2.與定點和直線的距離之比為定值e的點的軌跡.(0<e<1) |
2.與定點和直線的距離之比為定值e的點的軌跡.(e>1) |
與定點和直線的距離相等的點的軌跡. |
||
|
圖形 |
|
|
|
|
|
方 程 |
標準方程 |
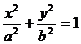 ( (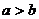 >0) >0) |
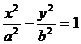 (a>0,b>0) (a>0,b>0) |
y2=2px |
|
參數方程 |
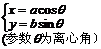 |
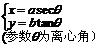 |
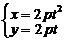 (t為參數) (t為參數) |
|
|
范圍 |
─a£x£a,─b£y£b |
|x| ³ a,yÎR |
x³0 |
|
|
中心 |
原點O(0,0) |
原點O(0,0) |
|
|
|
頂點 |
(a,0), (─a,0), (0,b) , (0,─b) |
(a,0), (─a,0) |
(0,0) |
|
|
對稱軸 |
x軸,y軸; 長軸長2a,短軸長2b |
x軸,y軸; 實軸長2a, 虛軸長2b. |
x軸 |
|
|
焦點 |
F1(c,0),
F2(─c,0) |
F1(c,0),
F2(─c,0) |
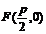 |
|
|
焦距 |
2c (c=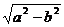 ) ) |
2c (c=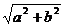 ) ) |
|
|
|
離心率 |
   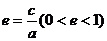 |
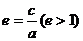 |
e=1 |
|
|
準線 |
x=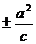 |
x=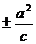 |
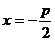 |
|
|
漸近線 |
|
y=±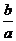 x x |
|
|
|
焦半徑 |
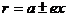 |
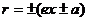 |
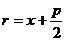 |
|
|
通徑 |
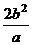 |
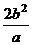 |
2p |
|
|
焦參數 |
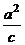 |
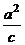 |
P |
4、曲線和方程
1.曲線與方程:在直角坐標系中,如果曲線C和方程f(x,y)=0的實數解建立了如下的關系:
(1) 曲線C上的點的坐標都是方程f(x,y)=0的解(純粹性);
(2) 方程f(x,y)=0的解為坐標的點都在曲線C上(完備性)。
則稱方程f(x,y)=0為曲線C的方程,曲線C叫做方程f(x,y)=0的曲線。
2.求曲線方程的方法:.
(1)待定系數法; (2) 直接法(直譯法);(3)定義法; (4)相關點代入法(轉移法);(5)參數法.
3.過兩條曲線f1(x,y)=0與f2(x,y)=0的公共點的曲線系方程:
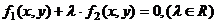
(二)考點預測題
1(2008年江蘇卷5).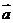 ,
,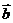 的夾角為
的夾角為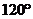 ,
,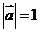 ,
,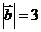 則
則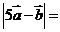 .
.
[解析]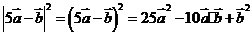 =
=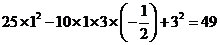 ,則
,則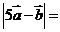 7.
7.
[答案]7.
2(2007年山東理11). 在直角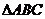 中,
中,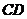 是斜邊
是斜邊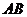 上的高,則下列等式不成立的是( )
上的高,則下列等式不成立的是( )
A.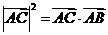 B.
B. 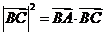
C.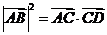 D.
D.
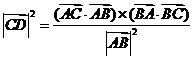
[解析]由于
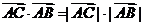 cso∠CAB=|
cso∠CAB=|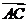 |2,
可排除A.
|2,
可排除A. 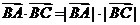 cos∠ABC=
cos∠ABC=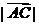 2,
可排除B , 而
2,
可排除B , 而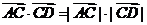 cos(π-∠ACD)=-|
cos(π-∠ACD)=-|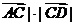 cos∠ACD<0 , |
cos∠ACD<0 , |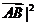 >0
, ∴|
>0
, ∴|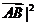 ≠
≠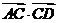 ,可知選C.
,可知選C.
[答案]C.
3(廣東省2009屆高三第一次六校聯考(理)16).已知向量a=(sinθ,1),b=(1,cosθ),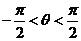 .
.
(Ⅰ)若a⊥b,求θ;
(Ⅱ)求|a+b|的最大值.
[解析](Ⅰ)若a⊥b,則sinθ+cosθ=0,
由此得 tanθ=-1(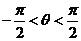 ),
),
所以 θ=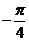 ;
;
(Ⅱ)由a=(sinθ,1),b=(1,cosθ),得
|a+b|==
=,
當sin(θ+)=1時,|a+b|取得最大值,
即當θ=時,|a+b|最大值為+1.
4(2009屆廣東五校高三第二聯考試卷文) .已知向量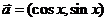 ,
,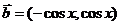 ,
,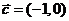 .
.
(1)若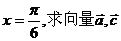 的夾角;
的夾角;
(2)當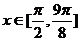 時,求函數
時,求函數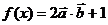 的最大值.
的最大值.
[解析](1)當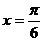 時,
時,
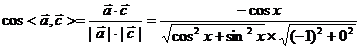
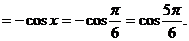
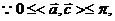
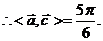
(2)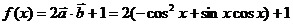
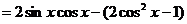
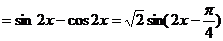 .
.

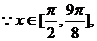 ∴
∴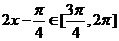 ,故
,故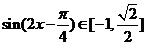
∴當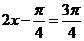 時,即
時,即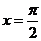 ,所以
,所以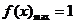 .
.
(一)文字介紹
預計向量基本概念、向量基本運算等基礎問題,通常為選擇題或填空題出現;而向量與三角函數、解三角形等綜合的問題,通常為解答題,難度以中檔題為主.具體如下:
1.向量概念和向量的基本定理
有關向量概念和向量的基本定理的命題,主要以選擇題或填空題為主,考查的難度屬中檔類型.
2.向量的運算
向量的運算要求掌握向量的加減法運算,會用平行四邊形法則、三角形法則進行向量的加減運算;掌握實數與向量的積運算,理解兩個向量共線的含義,會判斷兩個向量的平行關系;掌握向量的數量積的運算,體會平面向量的數量積與向量投影的關系,并理解其幾何意義,掌握數量積的坐標表達式,會進行平面向量積的運算,能運用數量積表示兩個向量的夾角,會用向量積判斷兩個平面向量的垂直關系.主要以選擇、填空題型出現,難度不大,考查重點為模和向量夾角的定義、夾角公式、向量的坐標運算,有時也會與其它內容相結合.
3.向量與三角函數的綜合問題
向量與三角函數的綜合問題是高考經常出現的問題,考查了向量的知識,三角函數的知識,達到了高考中試題的覆蓋面的要求.命題以三角函數作為坐標,以向量的坐標運算或向量與解三角形的內容相結合,也有向量與三角函數圖象平移結合的問題,屬中檔偏易題.
4.平面向量與函數問題的交匯
平面向量與函數交匯的問題,主要是向量與二次函數結合的問題為主,要注意自變量的取值范圍.命題多以解答題為主,屬中檔題.
1(漢沽一中2008~2009屆月考文9).已知平面向量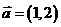 ,
, 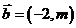 , 且
, 且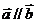 , 則
, 則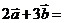 ( )
( )
A.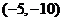 B.
B.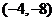 C.
C.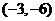 D.
D.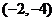
[解析]∵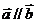 ,∴
,∴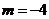 ,
,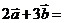
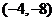 .
.
B.
 2(浙江省09年高考省教研室第一次抽樣測試數學試題(理)5).已知
2(浙江省09年高考省教研室第一次抽樣測試數學試題(理)5).已知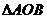 ,點P在直線AB上,且滿足
,點P在直線AB上,且滿足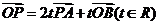 ,則
,則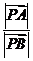 =( )
=( )
A、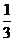 B、
B、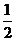 C、2
D、3
C、2
D、3
[解析]如圖所示,不妨設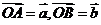 ;找共線,對于點P在直線AB上,有
;找共線,對于點P在直線AB上,有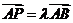 ;列方程,因此有
;列方程,因此有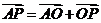
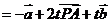 ,即
,即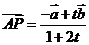 ;而
;而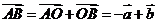 ,即有
,即有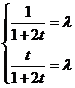 ,因此
,因此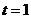 時
時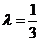 .即有
.即有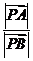 =
=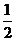 .
.
[答案]B.
3(沈陽二中2009屆高三期末數學試題).設點P是△ABC所在平面內一點,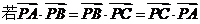 ,則點P是△ABC的( )
,則點P是△ABC的( )
A.內心 B.外心 C.重心 D.垂心
[解析]
[答案]D.
4(寧波市2008學年度第一學期高三期末數(文)).已知在平面直角坐標系中,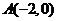 ,
,
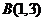 ,O為原點,且
,O為原點,且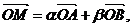 (其中
(其中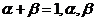 均為實數),若N(1,0),則
均為實數),若N(1,0),則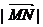 的最小值是 .
的最小值是 .
[解析]由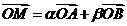 及
及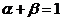 知,點M與點A、B共線,所以
知,點M與點A、B共線,所以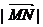 的最小值是點N到直線AB的距離,在直角三角形ABN中求解得
的最小值是點N到直線AB的距離,在直角三角形ABN中求解得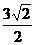 .
.
[答案]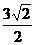 .
.
5(福州質檢·理).已知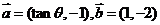 ,若
,若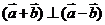 ,則
,則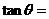 .
.
[解析]由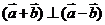 得:
得: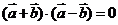 ,即
,即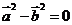 ,所以
,所以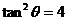 ,
,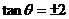 .
.
[答案]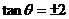 .
.
6(江蘇省南通市2008-2009學年度第一學期期末調研測試數學試卷13) .在△ABC中,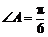 ,D是BC邊上任意一點(D與B、C不重合),且
,D是BC邊上任意一點(D與B、C不重合),且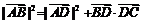 ,則
,則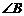 等于 ▲ .
等于 ▲ .
[解析]當點D無限逼近點C時,由條件知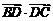 趨向于零,
趨向于零,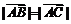 ,即△ABC是等邊三角形.
,即△ABC是等邊三角形.
[答案] 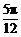 .
.
7 ( 江蘇省常州市2008-2009高三第一學期期中統一測試10) .已知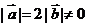 ,且關于
,且關于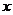 的函數
的函數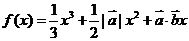 在R上有極值,則
在R上有極值,則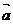 與
與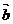 的夾角范圍為_______.
的夾角范圍為_______.
[解析]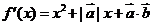 ,依題意
,依題意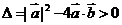 ,
,
即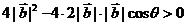 ,
,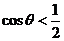 ,又夾角
,又夾角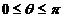 ,所以范圍為
,所以范圍為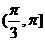 .
.
[答案]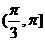 .
.
8(2008年東北三省三校高三第一次聯合模擬考試).
已知向量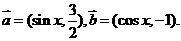
(1)當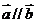 時,求
時,求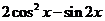 的值;
的值;
(2)求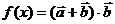 在
在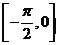 上的值域.
上的值域.
[解析](1)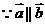 ,∴
,∴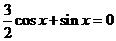 ,∴
,∴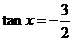
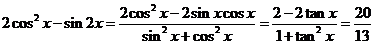 .
.
(2)
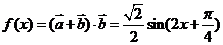
∵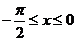 ,∴
,∴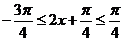 ,∴
,∴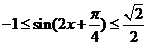
∴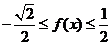 ∴函數
∴函數 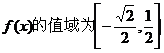 .
.
9(紹興市2008學年第一學期統考數學試題).已知向量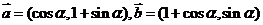 ,
,
(1)若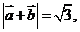 求
求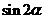 的值;
的值;
(2)設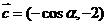 ,求
,求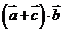 的取值范圍.
的取值范圍.
[解析](1)因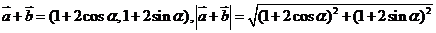
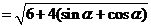 ,∴
,∴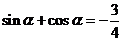 ,兩邊平方得
,兩邊平方得 ,
,
∴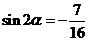 .
.
(2)因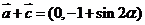 ,∴
,∴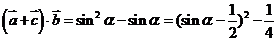
又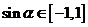 ,∴
,∴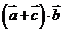 的取值范圍為
的取值范圍為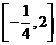 .
.
10 (溫州市十校2008學年高三第一學期期初聯考 數學試題(文)) .已知A、B、C三點的坐標分別為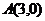 、
、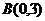 、
、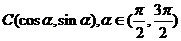 .
.
(1)若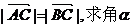 的值;
的值;
(2)若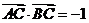 ,求
,求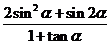 的值.
的值.
[解析](1) 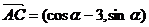
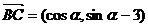
∵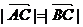 ∴
∴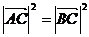
即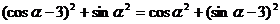
∴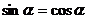 ,又∵
,又∵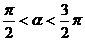 ,∴
,∴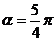 .
.
(2)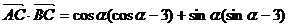
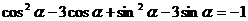 ,∴
,∴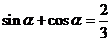 ,
,
兩邊平方,得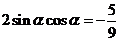 ,
,
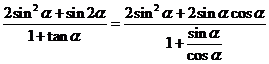
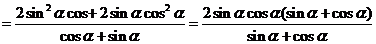
=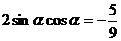 .
.
1(2008年安徽卷3).在平行四邊形ABCD中,AC為一條對角線,若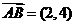 ,
,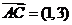 ,則
,則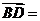 ( )
( )
A.(-2,-4) B.(-3,-5) C.(3,5) D.(2,4)
[解析]因為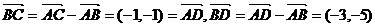 ,選B.
,選B.
[答案]B.
2(2007年山東文5).已知向量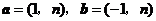 ,若
,若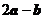 與
與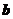 垂直,則
垂直,則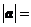 ( C )
( C )
A.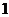 B.
B.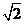 C.
C.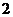 D.4
D.4
[解析]∵2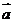 -
-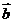 與
與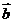 垂直. ∴(2
垂直. ∴(2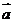 -
-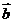 )·
)·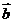 =0, 而2
=0, 而2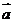 -
-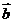 = (3 , n) , ∴-3+n2=0
, 而|
= (3 , n) , ∴-3+n2=0
, 而|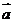 |2
=
|2
=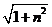 =
4 即 |
=
4 即 |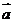 |=2
. 兩個非零向量
|=2
. 兩個非零向量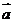 ⊥
⊥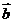
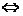
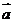 ·
·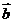 =0
=0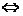 x1x2+y1y2=0
, |
x1x2+y1y2=0
, |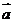 |2
=
|2
=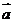 2
= x2 +y2.
2
= x2 +y2.
[答案]C.
3(2008年遼寧卷理5).已知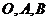 是平面上的三個點,直線
是平面上的三個點,直線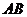 上有一點
上有一點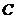 ,滿足
,滿足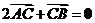 ,則
,則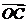 等于( )
等于( )
A.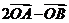 B.
B.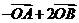 C.
C.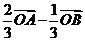 D.
D.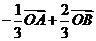
[解析]依題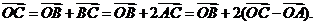 ∴
∴
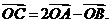
[答案]A.
4(2008年浙江卷理9).已知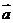 ,
,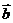 是平面內兩個互相垂直的單位向量,若向量
是平面內兩個互相垂直的單位向量,若向量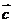 滿足
滿足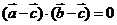 ,則
,則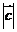 的最大值是( )
的最大值是( )
A. 1 B. 2 C. 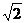 D.
D. 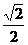
[解析]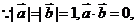
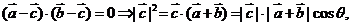
∴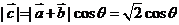 ,則
,則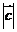 的最大值是
的最大值是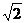 ;
;
∴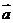 ,
,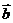 對應的點A,B在圓
對應的點A,B在圓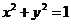 上,
上,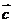 對應的點C在圓
對應的點C在圓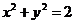 上即可.
上即可.
[答案]C.
5(2008年天津卷理14).如圖,在平行四邊形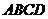 中,
中,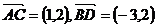 ,
,
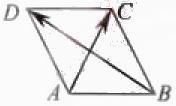 則
則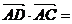 .
.
[解析]令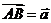 ,
,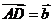 ,則
,則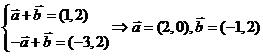
所以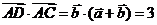 .
.
[答案]3.
6(2007年天津理15)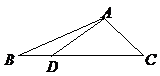 .如圖,在
.如圖,在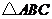 中,
中,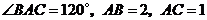 ,
,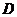 是邊
是邊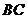 上一點,
上一點,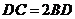 ,則
,則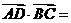 .
.
[解析]在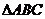 中,有余弦定理得
中,有余弦定理得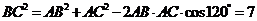 ,
,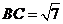 ,
,
由正弦定理得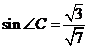 ,則
,則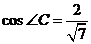 ,在
,在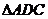 中,由余弦定理求得
中,由余弦定理求得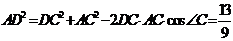 ,則
,則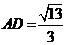 ,
,
由余弦定理得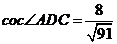 ,
,
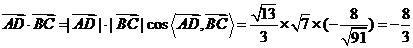 .
.
[答案] .
.
7(2007年廣東文16).已知ΔABC三個頂點的直角坐標分別為A(3,4)、B(0,0)、C(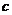 ,0).
,0).
(1)若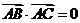 ,求
,求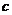 的值;
的值;
(2)若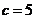 ,求sin∠A的值
,求sin∠A的值
[解析] (1) 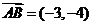 ,
,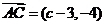 ,
,
由 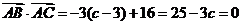 得
得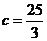 .
.
(2) 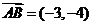 ,
,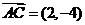 ,
,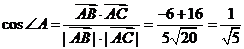 ,
,
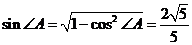 .
.
5.向量的應用
(1)會用向量方法解決某些簡單的平面幾何問題.
(2)會用向量方法解決簡單的力學問題與其他一些實際問題.
4.平面向量的數量積
(1)理解平面向量數量積的含義及其物理意義.
(2)了解平面向量的數量積與向量投影的關系.
(3)掌握數量積的坐標表達式,會進行平面向量數量積的運算.
(4)能運用數量積表示兩個向量的夾角,會用數量積判斷兩個平面向量的垂直關系.
3.平面向量的基本定理及坐標表示
(1) 了解平面向量的基本定理及其意義.
(2) 掌握平面向量的正交分解及其坐標表示.
(3)會用坐標表示平面向量的加法、減法與數乘運算.
(4) 理解用坐標表示的平面向量共線的條件.
2.向量的線性運算
(1) 掌握向量加法、減法的運算,并理解其幾何意義.
(2) 掌握向量數乘的運算及其幾何意義,理解兩個向量共線的含義.
(3) 了解向量線性運算的性質及其幾何意義.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com