日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

（福建卷文19）如圖，在四棱錐P—ABCD中，側面PAD⊥底面ABCD，側棱PA＝PD=,底面ABCD為直角梯形，其中BC∥AD,AB⊥AD,AD=2AB=2BC=2，O為AD中點.

(Ⅰ)求證:PO⊥平面ABCD；

(Ⅱ)求異面直線PB與CD所成角的余弦值；

(Ⅲ)求點A到平面PCD的距離.

（福建卷文19）如圖，在四棱錐P—ABCD中，側面PAD⊥底面ABCD，側棱PA＝PD=,底面ABCD為直角梯形，其中BC∥AD,AB⊥AD,AD=2AB=2BC=2，O為AD中點.

(Ⅰ)求證:PO⊥平面ABCD；

(Ⅱ)求異面直線PB與CD所成角的余弦值；

(Ⅲ)求點A到平面PCD的距離.

 (2012年高考福建卷理科19)（本小題滿分13分）

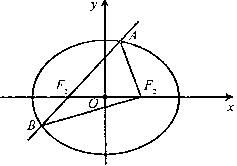如圖，橢圓的左焦點為，右焦點為，離心率。過的直線交橢圓于兩點，且的周長為8。

（Ⅰ）求橢圓的方程。

（Ⅱ）設動直線與橢圓有且只有一個公共點，且與直線相交于點。試探究：

     在坐標平面內是否存在定點，使得以為直徑的圓恒過點？若存在，求出點的坐標；若不存在，說明理由。

（06年福建卷理）對于直角坐標平面內的任意兩點，定義它們之間的一種“距離”：              給出下列三個命題：

       ①若點C在線段AB上，則

       ②在中，若則

       ③在中，

       其中真命題的個數為

       （A）0　　　　（B）1　　　　（C）2　　　　（D）3

（07年福建卷理） 已知集合，且，則實數的取值范圍是（    ）

A．             B．              C．            D．