日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

19.(本題滿分16分)

已知函數f(x)=alnx+x²(a為實常數).

(1)若a=－2，求證：函數f(x)在(1，+．∞)上是增函數；

(2)求函數f(x)在[1，e]上的最小值及相應的x值；

(3)若存在x∈[1，e]，使得f(x)≤(a+2)x成立，求實數a的取值范圍.

18.(本小題滿分16分)

設橢圓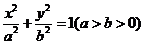的左焦點為F，上頂點為A，過點A且與AF垂直的光線經橢圓的右準線反射，反射光線與直線AF平行.

(1)求橢圓的離心率；

(2)設入射光線與右準線的交點為B，過A，B，F三點的圓恰好與直線3x一y+3=0相切，求橢圓的方程.

17.(本小題滿分14分)

在直角坐標系xoy中，若角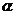的始邊為x軸的非負半軸，終邊為射線l：y=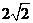x (x≥0).

(1)求的值；

(2)若點P，Q分別是角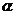始邊、終邊上的動點，且PQ=4，求△POQ面積最大時，點P，Q

的坐標．

16.(本小題滿分14分)

如圖，四邊形ABCD為矩形，BC上平面ABE，F為CE上的點，且BF⊥平面ACE.

(1)求證：AE⊥BE；

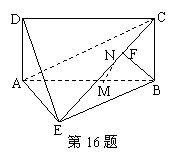(2)設點M為線段AB的中點，點N為線段CE的中點．

　 求證：MN∥平面DAE．

15.(本小題滿分14分)

　　 已知z，y之間的一組數據如下表：　

(1)從x ,y中各取一個數，求x+y≥10的概率；

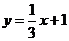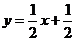(2)對于表中數據，甲、乙兩同學給出的擬合直線分別為與，試利

　 用“最小平方法(也稱最小二乘法)”判斷哪條直線擬合程度更好.

14.設函數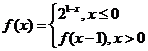,方程f(x)＝x+a有且只有兩相不等實數根，則實a的取值范圍為　　　　　　 .

13.已知數列{a_n}共有m項，記{a_n}的所有項和為s(1)，第二項及以后　 　　

所有項和為s(2)，第三項及以后所有項和為s(3)，…，第n項及以后所有項和為s(n)，若s(n)是首項為1，公差為2的等差數列的前n項和，則當n<m時，a_n =　　　　　 .

12.如圖，半徑為10 cm的圓形紙板內有一個相同圓心的半徑為1 cm的

　 小圓．現將半徑為1 cm的一枚硬幣拋到此紙板上，使硬幣整體隨機

　 落在紙板內，則硬幣落下后與小圓無公共點的概率為　　　　　 .

11.已知函數f(x)= 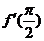sinx+cosx，則=　　　　　　 .

10.如圖，已知雙曲線以長方形ABCD的頂點A，B為左、右焦點，且過C，D兩頂點．若AB=4，BC=3，則此雙曲線的標準方程為　　　　　　 .