
4、某次乒乓球比賽的決賽在甲乙兩名選手之間舉行,比賽采用五局三勝制,按以往比賽經驗,甲勝乙的概率為 .
.
(Ⅰ)求比賽三局甲獲勝的概率;
(Ⅱ)求甲獲勝的概率;
(Ⅲ)設甲比賽的次數為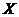 ,求
,求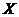 的數學期望.
的數學期望.
揚州市2008-2009學年度第一學期期未調研測試試題
3、如圖,四棱錐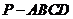 中,底面ABCD是矩形,
中,底面ABCD是矩形,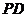 ⊥平面ABCD,且
⊥平面ABCD,且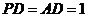 ,
,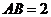 ,點E是AB上一點,AE等于何值時,二面角
,點E是AB上一點,AE等于何值時,二面角 的平面角為
的平面角為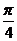 .
.
2、選修4-4 參數方程與極坐標
已知某圓錐曲線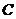 的參數方程為
的參數方程為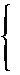
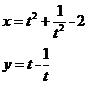 (
(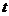 為參數).
為參數).
(Ⅰ)試將圓錐曲線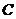 的參數方程化為普通方程;
的參數方程化為普通方程;
(Ⅱ)以圓錐曲線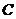 的焦點為極點,以它的對稱軸為極軸建立極坐標系,試求它的極坐標方程.
的焦點為極點,以它的對稱軸為極軸建立極坐標系,試求它的極坐標方程.
(總分40分,加試時間30分鐘)
答卷前,請考生務必將自己的學校、姓名、考試號等信息填寫在答卷密封線內.解答過程應寫在答題卷的相應位置上,在其它地方答題無效。
1、 選修4-2 矩陣與變換
選修4-2 矩陣與變換
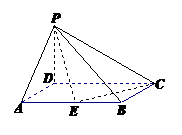
如圖矩形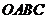 在變換
在變換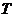 的作用下變成了平行四邊形
的作用下變成了平行四邊形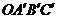 ,求變換
,求變換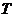 所對應的矩陣
所對應的矩陣 .
.
20.(本題滿分16分)
已知等差數列 的首項為
的首項為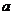 ,公差為
,公差為 ,等比數列
,等比數列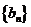 的首項為
的首項為 ,公比為
,公比為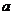 (其中
(其中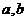 均為正整數).
均為正整數).
(Ⅰ) 若 ,求數列
,求數列 、
、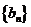 的通項公式;
的通項公式;
(Ⅱ)在(Ⅰ)的條件下,若
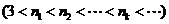 成等比數列,求數列
成等比數列,求數列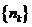 的通項公式;
的通項公式;
(Ⅲ) 若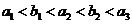 ,且至少存在三個不同的
,且至少存在三個不同的 值使得等式
值使得等式 成立,試求
成立,試求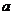 、
、 的值.
的值.
揚州市2008-2009學年度第一學期期未調研測試試題
高 三 數 學
19.(本小題滿分16分)
已知函數 .
.
(Ⅰ)若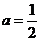 ,求
,求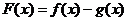 的單調區間;
的單調區間;
(Ⅱ)若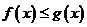 恒成立,求
恒成立,求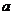 的取值范圍.
的取值范圍.
18、(本題滿分15分)
已知圓 交
交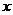 軸于
軸于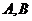 兩點,曲線
兩點,曲線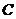 是以
是以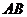 為長軸,直線
為長軸,直線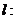
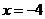 為準線的橢圓.
為準線的橢圓.
(Ⅰ)求橢圓的標準方程;
 (Ⅱ)若
(Ⅱ)若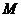 是直線
是直線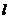 上的任意一點,以
上的任意一點,以 為直徑的圓
為直徑的圓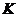 與圓
與圓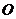 相交于
相交于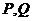 兩點,求證:直線
兩點,求證:直線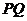 必過定點
必過定點 ,并求出點
,并求出點 的坐標;
的坐標;
(Ⅲ)如圖所示,若直線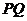 與橢圓
與橢圓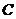 交于
交于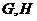 兩點,且
兩點,且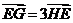 ,試求此時弦
,試求此時弦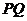 的長.
的長.
17、(本題滿分15分)
為了分析某個高三學生的學習狀態,對其下一階段的學習提供指導性建議。現對他前7次考試的數學成績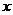 、物理成績
、物理成績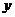 進行分析.下面是該生7次考試的成績.
進行分析.下面是該生7次考試的成績.
|
數學 |
88 |
83 |
117 |
92 |
108 |
100 |
112 |
|
物理 |
94 |
91 |
108 |
96 |
104 |
101 |
106 |
(Ⅰ)他的數學成績與物理成績哪個更穩定?請給出你的證明;
(Ⅱ)已知該生的物理成績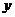 與數學成績
與數學成績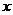 是線性相關的,若該生的物理成績達到115分,請你估計他的數學成績大約是多少?并請你根據物理成績與數學成績的相關性,給出該生在學習數學、物理上的合理建議.
是線性相關的,若該生的物理成績達到115分,請你估計他的數學成績大約是多少?并請你根據物理成績與數學成績的相關性,給出該生在學習數學、物理上的合理建議.
16.(本題滿分14分)
在正方體 中,
中,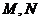 分別是
分別是 中點.
中點.
 (Ⅰ)求證:平面
(Ⅰ)求證:平面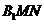 ⊥平面
⊥平面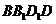 ;
;
(Ⅱ)若在棱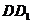 上有一點
上有一點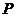 ,使
,使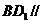 平面
平面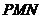 ,求
,求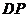 與
與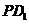 的比.
的比.
15.(本題滿分14分)
在△ABC中,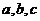 分別是角A,B,C的對邊,
分別是角A,B,C的對邊,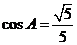 ,
,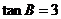 .
.
(Ⅰ)求角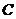 的值;
的值;
(Ⅱ)若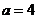 ,求△ABC面積.
,求△ABC面積.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com