
8.利用導數證明不等式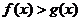 的步驟:
的步驟:
(1)作差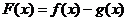 ;
;
(2)判斷函數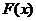 在定義域上的單調性并求它的最小值;
在定義域上的單調性并求它的最小值;
(3)判斷最小值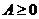 ;
;
(4)結論: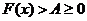 ,則
,則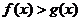 .
.
7.含有參數的函數求最值的方法:
看導數為0的點與定義域之間的關系.
6. 利用導數求最值的步驟:
(1)求函數在給定區間上的極值;
(2)比較區間端點所對的函數值與極值的大小,確定最大值與最小值.
5.求函數極值的方法:
(1)先找定義域,求導數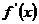 ;
;
 (2)求方程
(2)求方程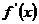 =0的根
=0的根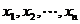 找出定義域的分界點;
找出定義域的分界點;
(3)列表,根據單調性求出極值.
已知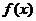 在
在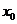 處的極值為A,相當于給出了兩個條件:①函數在此點導數值為零,②函數在此點的值為定值.
處的極值為A,相當于給出了兩個條件:①函數在此點導數值為零,②函數在此點的值為定值.
4.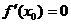 是函數f(x)在x0處取得極值的必要非充分條件,f(x)在x0處取得極值的充分必要條件是什么?
是函數f(x)在x0處取得極值的必要非充分條件,f(x)在x0處取得極值的充分必要條件是什么?
3.
利用導數可以證明或判斷函數的單調性,注意當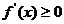 或
或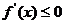 ,帶上等號.
,帶上等號.
例.已知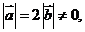 且關于
且關于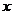 的函數
的函數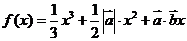 在R上有極值,則
在R上有極值,則 與
與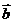 的夾角的范圍為
的夾角的范圍為
2.幾個重要函數的導數:
①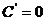 ,(C為常數)
②
,(C為常數)
②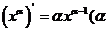 為常數)
為常數)
③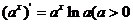 且
且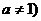 ④
④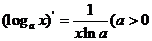 且
且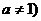
⑤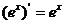 ⑥
⑥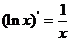
⑦ ⑧
⑧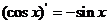
導數的四運算法則
①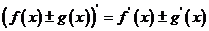
②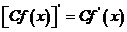 (C為常數)
(C為常數)
③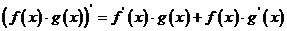
④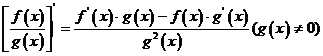
1.導數的幾何意義即曲線在該點處的切線的斜率,學會定義的多種變形.
8.一個封閉圖形首尾連接而成的向量和為零向量,這是題目中的天然條件,要注意運用,對于一個向量等式,可以移項,兩邊平方、兩邊同乘以一個實數,兩邊同時取模,兩邊同乘以 一個向量,但不能兩邊同除以一個向量.
例1.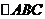 內接于以O為圓心,1為半徑的圓,且
內接于以O為圓心,1為半徑的圓,且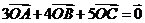 ,求數量積
,求數量積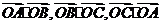 .
.
 例2.平面四邊形ABCD中,
例2.平面四邊形ABCD中,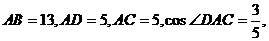
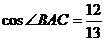 ,設
,設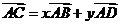 ,求
,求 的值.
的值.
例3.如圖,設點O在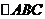 內部,且有
內部,且有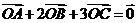 ,則
,則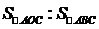 = ____.
= ____.
7.向量等式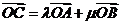 的常見變形方法:(1)兩邊同時平方;(2)兩邊同時乘以一個向量;(3)合并成兩個新向量間的線性關系.
的常見變形方法:(1)兩邊同時平方;(2)兩邊同時乘以一個向量;(3)合并成兩個新向量間的線性關系.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com