
1.已知集合A={x|-2,-1,0,1,2},B={2,3},則A∪B為( )
A.{2} B.{2,3} C.{-2,-1,0,1,2} D.{-2,-1,0,1,2,3}
21.方差的性質
若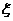 -
-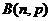 ,則
,則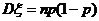 .
.
20.標準差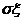 =
=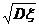 .
.
19.方差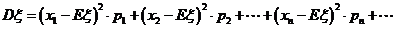
例題.設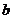 和
和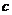 分別是先后拋擲一枚骰子得到的點數,用隨機變量
分別是先后拋擲一枚骰子得到的點數,用隨機變量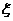 表示方程
表示方程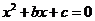 實根的個數(重根按一個計).
實根的個數(重根按一個計).
(1)求方程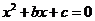 有實根的概率;
有實根的概率;
(2)求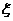 的分布列和數學期望;
的分布列和數學期望;
(3)求在先后兩次出現的點數中有5的條件下,方程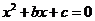 有實根的概率.
有實根的概率.
解析: (1)基本事件總數為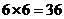 ,
,
若使方程有實根,則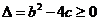 ,即
,即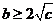 .
.
當 時,
時,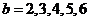 ;當
;當 時,
時,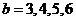 ;當
;當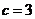 時,
時,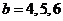 ;
;
當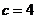 時,
時,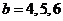 ;當
;當 時,
時,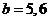 ;當
;當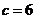 時,
時,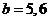 ,
,
目標事件個數為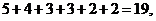
因此方程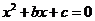 有實根的概率為
有實根的概率為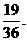
(2)由題意知,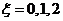 ,則
,則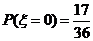 ,
,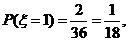
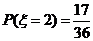 ,
,
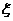 |
0 |
1 |
2 |
|
P |
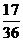 |
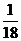 |
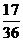 |
故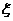 的分布列為
的分布列為

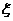 的數學期望
的數學期望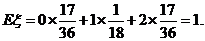
(3)記“先后兩次出現的點數中有5”為事件M,“方程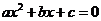 有實根” 為事件N,則
有實根” 為事件N,則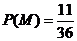 ,
,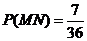 ,
,
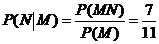 .
.
例題:袋中裝有3個白球和4個黑球,現從袋中任取3個球,設ξ為所取出的3個球中白球的個數.
(I)求ξ的概率分布; (II)求Eξ.
解:(I)ξ的可能取值為0,1,2,3.
∵P(ξ=0)=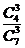 =
=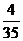 ; P(ξ=1)=
; P(ξ=1)=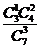 =
=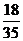 ;
;
P(ξ=2)=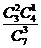 =
=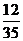 ; P(ξ=3)=
; P(ξ=3)=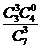 =
=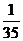 .
.
∴ξ的分布列為:
|
ξ |
0 |
1 |
2 |
3 |
|
P |
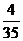 |
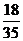 |
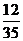 |
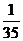 |
(II)Eξ=0×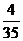 +1×
+1×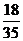 +2×
+2×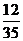 +3×
+3×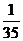 =
=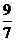 .
.
18.數學期望的性質
(1)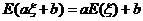 .(2)若
.(2)若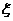 -
-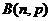 ,則
,則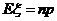 .
.
(3) 若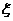 服從幾何分布,且
服從幾何分布,且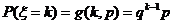 ,則
,則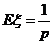 .
.
17.數學期望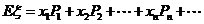
16.離散型隨機變量的分布列的兩個性質:(1)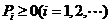 ;(2)
;(2)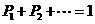 .
.
15.n次獨立重復試驗中某事件恰好發生k次的概率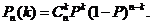
14.n個獨立事件同時發生的概率 P(A1· A2·…· An)=P(A1)· P(A2)·…· P(An).
13.獨立事件A,B同時發生的概率P(A·B)= P(A)·P(B).
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com