
2.(2005湖北)雙曲線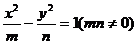 離心率為2,有一個焦點與拋物線
離心率為2,有一個焦點與拋物線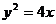 的焦點重合,則mn的值為 ( )
的焦點重合,則mn的值為 ( )
A.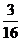 B.
B.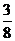 C.
C.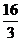 D.
D.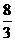
1.(2004湖北)已知橢圓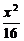 +
+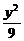 =1的左、右焦點分別為F1、F2,點P在橢圓上,若P、F1、F2是一個直角三角形的三個頂點,則點P到x軸的距離為 ( )
=1的左、右焦點分別為F1、F2,點P在橢圓上,若P、F1、F2是一個直角三角形的三個頂點,則點P到x軸的距離為 ( )
A.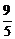 B.3
C.
B.3
C.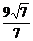 D.
D.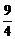
5.注意用好以下數學思想、方法:
①數形結合思想;②方程與函數思想;③化歸轉化思想;④分類討論思想;⑤對稱思想;⑥主元與參數思想.此外,整體思想、正難則反思想、構造思想等也是解析幾何解題中不可缺少的思想方法.在復習中必須給予足夠的重視,真正發揮其聯系知識、簡化計算、提高能力中的作用.
同步練習 8.5 圓錐曲線綜合應用
[選擇題]
4.四點重視:①重視定義在解題中的作用;②重視平面幾何知識在解題中的簡化功能;③重視根與系數關系在解題中的作用;④重視曲線的幾何特征與方程的代數特征的統一.
3. 解決圓錐曲線應用問題時,要善于抓住問題的實質,通過建立數學模型,實現應用性問題向數學問題的順利轉化;要注意認真分析數量間的關系,緊扣圓錐曲線概念,充分利用曲線的幾何性質,確定正確的問題解決途徑,靈活運用解析幾何的常用數學方法,求得最終完整的解答.
2.對于求曲線方程中參數范圍或最值問題,應根據題設條件及曲線的幾何性質構造參數滿足的不等式,通過解不等式求得參數的范圍;或建立關于參數的目標函數,轉化為函數的值域來解,還有Δ法,幾何法,向量法等.
1.解決圓錐曲線的綜合問題應根據曲線的幾何特征,熟練運用圓錐曲線的知識將曲線的幾何特征轉化為數量關系,再結合代數等知識來解。
[例1](2006福建) 已知橢圓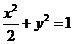 的左焦點為F,O為坐標原點。
的左焦點為F,O為坐標原點。
(I)求過點O、F,并且與橢圓的左準線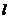 相切的圓的方程;
相切的圓的方程;
(II)設過點F且不與坐標軸垂直的直線交橢圓于A、B兩點,線段AB的垂直平分線與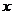 軸交于點G,求點G橫坐標的取值范圍。
軸交于點G,求點G橫坐標的取值范圍。
解:(I)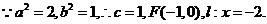
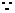 圓過點O、F,
圓過點O、F,
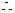 圓心M在直線
圓心M在直線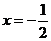 上。
上。
設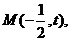 則圓半徑
則圓半徑
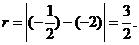
由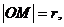 得
得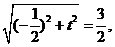
解得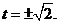
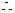 所求圓的方程為
所求圓的方程為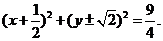
(II)設直線AB的方程為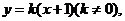
代入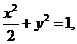 整理得
整理得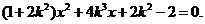
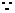 直線AB過橢圓的左焦點F,
直線AB過橢圓的左焦點F,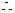 方程有兩個不等實根。
方程有兩個不等實根。
記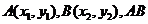 中點
中點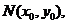
則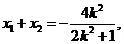
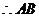 的垂直平分線NG的方程為
的垂直平分線NG的方程為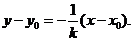
令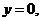 得
得

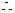 點G橫坐標的取值范圍為
點G橫坐標的取值范圍為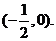
[例2](2006天津)如圖,以橢圓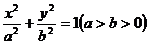 的中心
的中心 為圓心,分別以
為圓心,分別以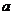 和
和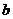 為半徑作大圓和小圓。過橢圓右焦點
為半徑作大圓和小圓。過橢圓右焦點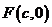
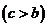 作垂直于
作垂直于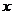 軸的直線交大圓于第一象限內的點
軸的直線交大圓于第一象限內的點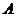 .連結
.連結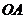 交小圓于點
交小圓于點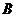 .設直線
.設直線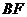 是小圓的切線.
是小圓的切線.
 (1)證明
(1)證明 ,并求直線
,并求直線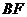 與
與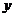 軸的交
軸的交
點 的坐標;
的坐標;
(2)設直線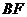 交橢圓于
交橢圓于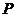 、
、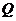 兩點,證明
兩點,證明
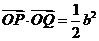 .
.
(Ⅰ)證明:由題設條件知,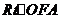 ∽
∽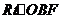 故
故
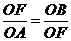 ,即
,即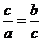
因此,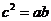 ①
①
解:在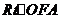 中
中
 .
.
于是,直線OA的斜率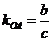 .設直線BF的斜率為
.設直線BF的斜率為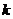 ,則
,則
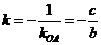 .
.
這時,直線BF與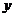 軸的交點為
軸的交點為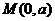
(Ⅱ)證明:由(Ⅰ),得直線BF得方程為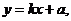 且
且
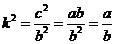 ②
②
由已知,設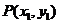 、
、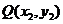 ,則它們的坐標滿足方程組
,則它們的坐標滿足方程組
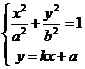 ③
③
由方程組③消去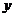 ,并整理得
,并整理得
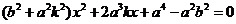 ④
④
由式①、②和④,
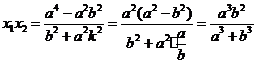
由方程組③消去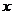 ,并整理得
,并整理得
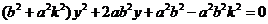 ⑤
⑤
由式②和⑤,
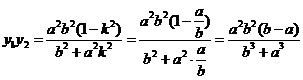
綜上,得到
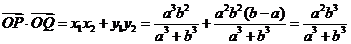
注意到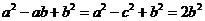 ,得
,得
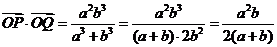

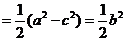
[例3]A、B、C是我方三個炮兵陣地,A在B正東6 km,C在B正北偏西30°,相距4 km,P為敵炮陣地,某時刻A處發現敵炮陣地的某種信號,由于B、C兩地比A距P地遠,因此4 s后,B、C才同時發現這一信號,此信號的傳播速度為1 km/s,A若炮擊P地,求炮擊的方位角.
解:如下圖,以直線BA為x軸,線段BA的中垂線為y軸建立坐標系,則
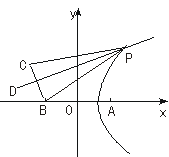 B(-3,0)、A(3,0)、C(-5,2
B(-3,0)、A(3,0)、C(-5,2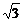 ).
).
因為|PB|=|PC|,所以點P在線段BC的垂直平分線上.
因為kBC=-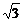 ,BC中點D(-4,
,BC中點D(-4,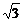 ),
),
所以直線PD的方程為y-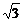 =
=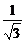 (x+4) ①
(x+4) ①
又|PB|-|PA|=4,故P在以A、B為焦點的雙曲線右支上.
設P(x,y),則雙曲線方程為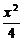 -
-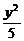 =1(x≥0) ②
=1(x≥0) ②
聯立①②,得x=8,y=5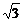 ,
,
所以P(8,5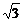 ).因此kPA=
).因此kPA=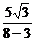 =
=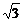 .
.
故炮擊的方位角為北偏東30°.
[例4] (2006春上海) 學校科技小組在計算機上模擬航天器變軌返回試驗. 設計方案如圖:航天器運行(按順時針方向)的軌跡方程為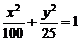 ,變軌(即航天器運行軌跡由橢圓變為拋物線)后返回的軌跡是以
,變軌(即航天器運行軌跡由橢圓變為拋物線)后返回的軌跡是以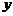 軸為對稱軸、
軸為對稱軸、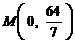 為頂點的拋物線的實線部分,降落點為
為頂點的拋物線的實線部分,降落點為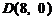 . 觀測點
. 觀測點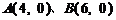 同時跟蹤航天器.
同時跟蹤航天器.
 (1)求航天器變軌后的運行軌跡所在的曲線方程;
(1)求航天器變軌后的運行軌跡所在的曲線方程;
(2)試問:當航天器在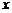 軸上方時,觀測點
軸上方時,觀測點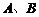 測得離航天器的距離分別為多少時,應向航天器發出變軌指令?
測得離航天器的距離分別為多少時,應向航天器發出變軌指令?
解(1)設曲線方程為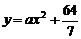 , 由題意可知,
, 由題意可知,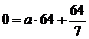 .
. 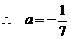 .
.
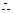 曲線方程為
曲線方程為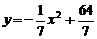
(2)設變軌點為 ,根據題意可知
,根據題意可知
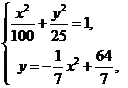 得
得
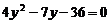 ,
,
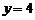 或
或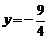 (不合題意,舍去).
(不合題意,舍去).
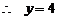 . 得
. 得 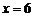 或
或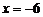 (不合題意,舍去).
(不合題意,舍去).
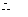
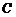 點的坐標為
點的坐標為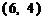 ,
, 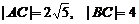 .
.
答:當觀測點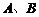 測得
測得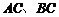 距離分別為
距離分別為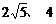 時,應向航天器發出變軌指令.
時,應向航天器發出變軌指令.
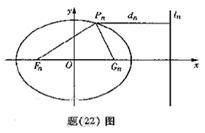
[研討.欣賞](2006重慶)已知一列橢圓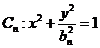 ,
,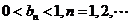 。若橢圓
。若橢圓 上有一點
上有一點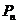 ,使
,使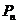 到右準線
到右準線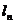 的距離
的距離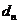 是
是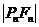 與
與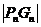 的等差中項,其中
的等差中項,其中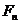 、
、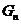 分別是
分別是 的左、右焦點。
的左、右焦點。
(Ⅰ)試證: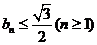 ;
;
 (Ⅱ)取
(Ⅱ)取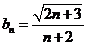 ,并用
,并用 表示
表示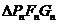 的面積,試證:
的面積,試證: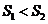 且
且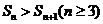
證:(I)由題設及橢圓的幾何性質有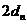
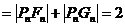 ,故
,故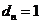 。
。
設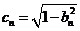 ,則右準線方程為
,則右準線方程為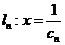 .
.
 因此,由題意
因此,由題意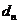 應滿足
應滿足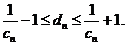 即
即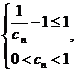 解之得:
解之得: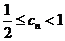 。
。
即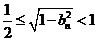 ,從而對任意
,從而對任意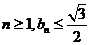 .
.
(II)設點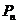 的坐標為
的坐標為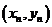 ,則由
,則由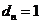 及橢圓方程易知
及橢圓方程易知

 。
。
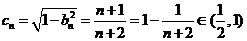
因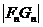
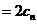 ,故
,故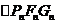 的面積為
的面積為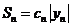 ,
,
從而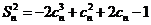 。
。
令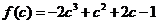 。由
。由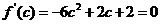 ,得兩根
,得兩根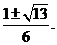 從而易知函數
從而易知函數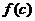 在
在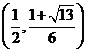 內是增函數。而在
內是增函數。而在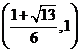 內是減函數。
內是減函數。
現在由題設取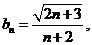 則
則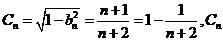 是增數列。
是增數列。
又易知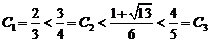 。
。
故由前已證,知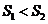 ,且
,且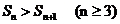 。
。
說明:如果建立Sn與n的函數,討論單調性比較復雜.
5.2; 6.  +
+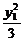 =1,
=1, 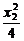 +
+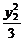 =1.相減得
=1.相減得
∴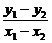 =-
=-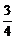 ·
·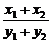 .
.
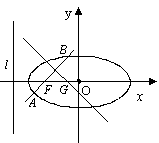
又∵M為AB中點,x1+x2=2,y1+y2=2.
∴直線l的斜率為-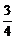 .
.
得直線l的方程為3x+4y-7=0.
4.設左焦點為F1,右焦點為F2,由雙曲線定義和三角形邊的關系得:

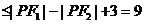 ,選D
,選D
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com