
3.已知向量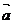 =(1,2)和
=(1,2)和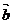 =(x,1),若向量
=(x,1),若向量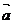 +2
+2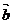 與2
與2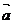 -
-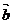 平行,則實數x等于 ( ▲ )
平行,則實數x等于 ( ▲ )
A.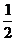 B.1 C.
B.1 C.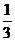 D.2
D.2
2.已知數列{an}是公差為2的等差數列,且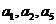 成等比數列,則
成等比數列,則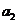 為 ( ▲ )
為 ( ▲ )
A.-2 B.-3 C.2 D.3
一項是符合題目要求的)
1.若M={1,2},N={2,3},則M∪N= ( ▲ )
A.{1,2,3} B.{2} C.{1,2,4} D.{4}
23.已知方程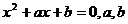 為常數。
為常數。
(Ⅰ)若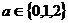 ,
,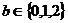 ,求方程的解的個數
,求方程的解的個數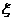 的期望;
的期望;
(Ⅱ)若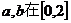 內等可能取值,求此方程有實根的概率.
內等可能取值,求此方程有實根的概率.
22。正方體ABCD-A1B1C1D1的棱長為2,點E為A1A的中點。
 (Ⅰ)求
(Ⅰ)求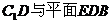 所成角的大小;
所成角的大小;
(Ⅱ)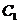 到平面
到平面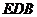 的距離。
的距離。
21.(選做題)從A,B,C,D四個中選做2個,每題10分,共20分.
A.選修4-1 幾何證明選講
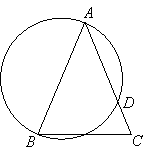
如圖,在△ABC中,AB=AC,以AB為直徑的圓
交AC于D.求證: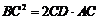 .
.
B.選修4-2 矩陣與變換
已知矩陣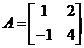 ,求
,求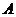 特征值λ1,λ2及對應的特征向量α1,α2.
特征值λ1,λ2及對應的特征向量α1,α2.
C.選修4-4 參數方程與極坐標
已知直線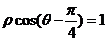 和圓
和圓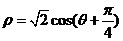 ,判斷直線和圓的位置關系.
,判斷直線和圓的位置關系.
D.選修4-5 不等式證明選講
若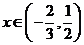 ,證明
,證明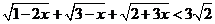 。
。
必做題(每題10分,共20分)
20.解:(Ⅰ)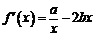 ,
,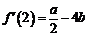 ,
, .
.
∴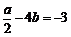 ,且
,且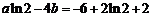 . …………………… 2分
. …………………… 2分
解得a=2,b=1. …………………… 4分
(Ⅱ) ,令
,令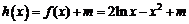 ,
,
則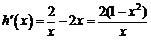 ,令
,令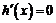 ,得x=1(x=-1舍去).
,得x=1(x=-1舍去).
在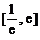 內,當x∈
內,當x∈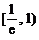 時,
時,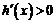 ,∴h(x)是增函數;
,∴h(x)是增函數;
當x∈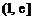 時,
時,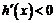 ,∴h(x)是減函數. …………………… 7分
,∴h(x)是減函數. …………………… 7分
則方程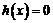 在
在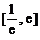 內有兩個不等實根的充要條件是
內有兩個不等實根的充要條件是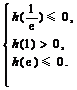 ……10分
……10分
即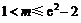 . …………………… 12分
. …………………… 12分
(Ⅲ)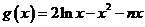 ,
,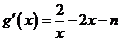 .
.
假設結論成立,則有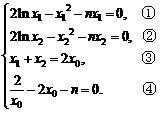
①-②,得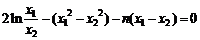 .
.
∴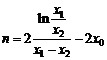 .
.
由④得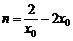 ,
,
∴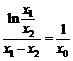 .即
.即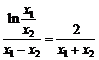 .
.
即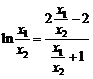 .⑤
…………………… 14分
.⑤
…………………… 14分
令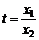 ,
,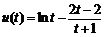 (0<t<1),
(0<t<1),
則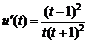 >0.∴
>0.∴ 在0<t<1上增函數.
在0<t<1上增函數.
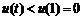 ,∴⑤式不成立,與假設矛盾.
,∴⑤式不成立,與假設矛盾.
∴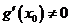 .
………………………………… 16分
.
………………………………… 16分
數 學(附加題)
20.(本小題滿分16分)
已知函數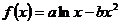 圖象上一點P(2,f(2))處的切線方程為
圖象上一點P(2,f(2))處的切線方程為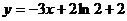 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若方程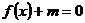 在
在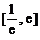 內有兩個不等實根,求
內有兩個不等實根,求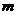 的取值范圍(其中
的取值范圍(其中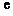 為自然對數的底,
為自然對數的底, );
);
(Ⅲ)令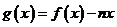 ,如果
,如果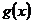 圖象與
圖象與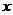 軸交于
軸交于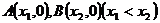 ,AB中點為
,AB中點為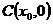 ,求證:
,求證: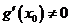 .
.
19.解:(Ⅰ)點A代入圓C方程,
 得
得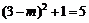 .
.
∵m<3,∴m=1. …… 2分
圓C: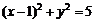 .
.
設直線PF1的斜率為k,
則PF1: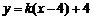 ,
,
即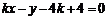 .
.
∵直線PF1與圓C相切,
∴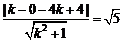 .
.
解得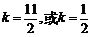 . …………………… 4分
. …………………… 4分
當k=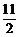 時,直線PF1與x軸的交點橫坐標為
時,直線PF1與x軸的交點橫坐標為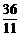 ,不合題意,舍去.
,不合題意,舍去.
當k=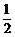 時,直線PF1與x軸的交點橫坐標為-4,
時,直線PF1與x軸的交點橫坐標為-4,
∴c=4.F1(-4,0),F2(4,0). …………………… 6分
2a=AF1+AF2=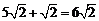 ,
,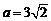 ,a2=18,b2=2.
,a2=18,b2=2.
橢圓E的方程為: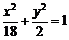 .
…………………… 8分2
.
…………………… 8分2
(Ⅱ)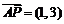 ,設Q(x,y),
,設Q(x,y),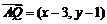 ,
,
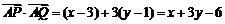 .
…………………… 10分
.
…………………… 10分
∵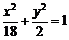 ,即
,即 ,
,
而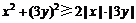 ,∴-18≤6xy≤18.
…………………… 12分
,∴-18≤6xy≤18.
…………………… 12分
則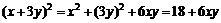 的取值范圍是[0,36]. ……… 14分
的取值范圍是[0,36]. ……… 14分
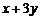 的取值范圍是[-6,6].
的取值范圍是[-6,6].
∴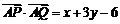 的取值范圍是[-12,0]. …………………… 16分
的取值范圍是[-12,0]. …………………… 16分
19.(本小題滿分16分)
已知點P(4,4),圓C: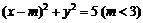 與橢圓E:
與橢圓E: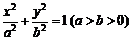 有一個公共點A(3,1),F1、F2分別是橢圓的左、右焦點,直線PF1與圓C相切.
有一個公共點A(3,1),F1、F2分別是橢圓的左、右焦點,直線PF1與圓C相切.
(Ⅰ)求m的值與橢圓E的方程;
(Ⅱ)設Q為橢圓E上的一個動點,求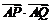 的取值范圍.
的取值范圍.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com