
題目列表(包括答案和解析)
某地區為了解中學生的日平均睡眠時間(單位:h),隨機選擇了n位中學生進行調查,根據所得數據畫出樣本的頻率分布直方圖如圖所示,且從左到右的第1個、第4個、第2個、第3個小長方形的面積依次構成公差為0.1的等差數列,又第一小組的頻數是10,則n=
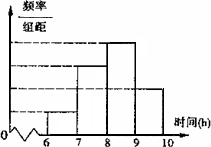
80
90
100
110
我們用min{S1,S2,…,Sn}和max{S1,S2,…,Sn}分別表示實數S1,S2,…,Sn中的最小者和最大者.
(1)設f(x)=min{sinx,cosx},g(x)=max{sinx,cosx},x∈[0,2π],函數f(x)的值域為A,函數g(x)的值域為B,求A∩B;
(2)數學課上老師提出了下面的問題:設a1,a2,an為實數,x∈R,求函數![]() (x1<x2<xn∈R=的最小值或最大值.為了方便探究,遵循從特殊到一般的原則,老師讓學生先解決兩個特例:求函數
(x1<x2<xn∈R=的最小值或最大值.為了方便探究,遵循從特殊到一般的原則,老師讓學生先解決兩個特例:求函數![]() 和
和![]() 的最值.學生甲得出的結論是:[f(x)]min=min{f(-2),f(-1),f(1)},且f(x)無最大值.學生乙得出的結論是:[g(x)]max=max{g(-1),g(1),g(2)},且g(x)無最小值.請選擇兩個學生得出的結論中的一個,說明其成立的理由;
的最值.學生甲得出的結論是:[f(x)]min=min{f(-2),f(-1),f(1)},且f(x)無最大值.學生乙得出的結論是:[g(x)]max=max{g(-1),g(1),g(2)},且g(x)無最小值.請選擇兩個學生得出的結論中的一個,說明其成立的理由;
(3)試對老師提出的問題進行研究,寫出你所得到的結論并加以證明(如果結論是分類的,請選擇一種情況加以證明).
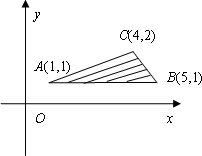
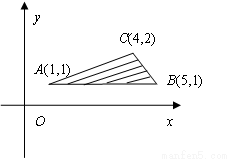
在如下圖所示的坐標平面的可行域內(陰影部分且包括邊界),目標函數:z=x+ay取得最小值的最優解有無數個,則![]() 的最大值是
的最大值是
A.2
B.![]()
C.![]()
D.![]()
對定義域分別是Df、Dg的函數y=f(x)、y=g(x),規定:函數h(x)
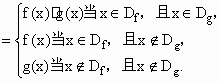
(1)若函數f(x)=![]() ,g(x)=x2,寫出函數h(x)的解析式;
,g(x)=x2,寫出函數h(x)的解析式;
(2)求問題(1)中函數h(x)的值域;
(3)若g(x)=f(x+α),其中α是常數,且a∈[0,π],請設計一個定義域為R的函數y=f(x),及一個α的值,使得h(x)=cos 4x,并予以證明.
在如下圖所示的坐標平面的可行域內(陰影部分且包括邊界),目標函數:z=x+ay取得最小值的最優解有無數個,則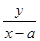 的最大值是 ( )
的最大值是 ( )
A.2 B.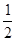 C.
C.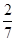 D.
D.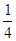
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com