
18.解:(Ⅰ)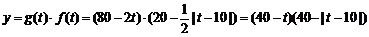 …… 4分
…… 4分
=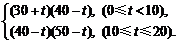 …………………… 8分
…………………… 8分
(Ⅱ)當0≤t<10時,y的取值范圍是[1200,1225],
在t=5時,y取得最大值為1225; …………………… 11分
當10≤t≤20時,y的取值范圍是[600,1200],
在t=20時,y取得最小值為600. …………………… 14分
(答)總之,第5天,日銷售額y取得最大為1225元;
第20天,日銷售額y取得最小為600元. …………………… 15分
18.(本小題滿分15分)
經市場調查,某超市的一種小商品在過去的近20天內的銷售量(件)與價格(元)均為時間t(天)的函數,且銷售量近似滿足g(t)=80-2t(件),價格近似滿足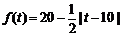 (元).
(元).
(Ⅰ)試寫出該種商品的日銷售額y與時間t(0≤t≤20)的函數表達式;
(Ⅱ)求該種商品的日銷售額y的最大值與最小值.
17.解:(Ⅰ)在Rt△ABC中,AB=1,
∠BAC=60°,∴BC=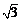 ,AC=2.
,AC=2.
在Rt△ACD中,AC=2,∠CAD=60°,
∴CD=2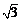 ,AD=4.
,AD=4.
∴SABCD=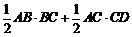
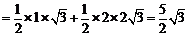 .……………… 3分
.……………… 3分
則V=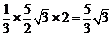 . ……………… 5分
. ……………… 5分
 (Ⅱ)∵PA=CA,F為PC的中點,
(Ⅱ)∵PA=CA,F為PC的中點,
∴AF⊥PC. ……………… 7分
∵PA⊥平面ABCD,∴PA⊥CD.
∵AC⊥CD,PA∩AC=A,
∴CD⊥平面PAC.∴CD⊥PC.
∵E為PD中點,F為PC中點,
∴EF∥CD.則EF⊥PC. ……… 9分
∵AF∩EF=F,∴PC⊥平面AEF.…… 10分
(Ⅲ)證法一:
取AD中點M,連EM,CM.則EM∥PA.
∵EM 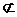 平面PAB,PA
平面PAB,PA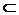 平面PAB,
平面PAB,
∴EM∥平面PAB. ……… 12分
在Rt△ACD中,∠CAD=60°,AC=AM=2,
∴∠ACM=60°.而∠BAC=60°,∴MC∥AB.
 ∵MC
∵MC 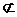 平面PAB,AB
平面PAB,AB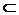 平面PAB,
平面PAB,
∴MC∥平面PAB. ……… 14分
∵EM∩MC=M,
∴平面EMC∥平面PAB.
∵EC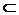 平面EMC,
平面EMC,
∴EC∥平面PAB. ……… 15分
證法二:
延長DC、AB,設它們交于點N,連PN.
∵∠NAC=∠DAC=60°,AC⊥CD,
∴C為ND的中點. ……12分
∵E為PD中點,∴EC∥PN.……14分
∵EC 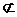 平面PAB,PN
平面PAB,PN 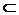 平面PAB,
平面PAB,
∴EC∥平面PAB. ……… 15分
17.(本小題滿分15分)
 在四棱錐P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E為PD的中點,PA=2AB=2.
在四棱錐P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E為PD的中點,PA=2AB=2.
(Ⅰ)求四棱錐P-ABCD的體積V;
(Ⅱ)若F為PC的中點,求證PC⊥平面AEF;
(Ⅲ)求證CE∥平面PAB.
16.解:(Ⅰ)n≥2時, . ………………… 4分
. ………………… 4分
n=1時,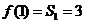 ,適合上式,
,適合上式,
∴
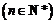 .
………………… 5分
.
………………… 5分
(Ⅱ)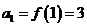 ,
,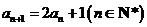 .
………………… 8分
.
………………… 8分
即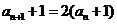 .
.
∴數列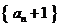 是首項為4、公比為2的等比數列. ………………… 10分
是首項為4、公比為2的等比數列. ………………… 10分
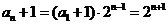 ,∴
,∴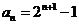
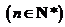 .……………… 12分
.……………… 12分
Tn=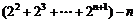 =
=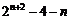 .
………………… 14分
.
………………… 14分
16.(本小題滿分14分)
已知數列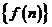 的前n項和為
的前n項和為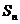 ,且
,且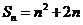 .
.
(Ⅰ)求數列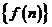 通項公式;
通項公式;
(Ⅱ)若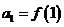 ,
,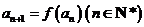 ,求證數列
,求證數列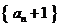 是等比數列,并求數列
是等比數列,并求數列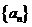 的前
的前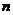 項和
項和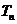 .
.
15.解:(Ⅰ) =
=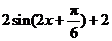 .………… 4分
.………… 4分
由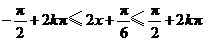 ,得
,得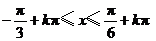 .
.
∴函數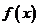 的單調增區間為
的單調增區間為
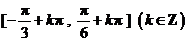 .………… 7分
.………… 7分
(Ⅱ)由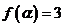 ,得
,得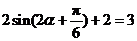 .
.
∴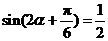 .
………………………………………… 10分
.
………………………………………… 10分
∴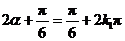 ,或
,或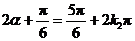
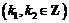 ,
,
即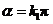 或
或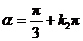
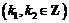 .
.
∵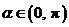 ,∴
,∴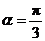 . …………………………………………… 14分
. …………………………………………… 14分
15.(本小題滿分14分)
已知函數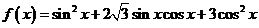 .
.
(Ⅰ)求函數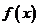 的單調增區間;
的單調增區間;
(Ⅱ)已知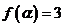 ,且
,且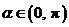 ,求α的值.
,求α的值.
14.已知命題:“在等差數列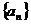 中,若
中,若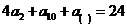 ,則
,則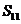 為定值”為真命題,由于印刷問題,括號處的數模糊不清,可推得括號內的數為_________.18
為定值”為真命題,由于印刷問題,括號處的數模糊不清,可推得括號內的數為_________.18
13.在銳角△ABC中,b=2,B=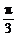 ,
,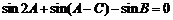 ,則△ABC的面積為_________.
,則△ABC的面積為_________.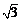
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com