
6. 直線l過點M(1,1),與橢圓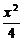 +
+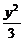 =1相交于A、B兩點,若AB的中點為M,則直線l的方程是________.
=1相交于A、B兩點,若AB的中點為M,則直線l的方程是________.
簡答:1-4.BCBD;
5.(2005山東)設直線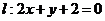 關于原點對稱的直線為
關于原點對稱的直線為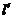 ,若
,若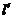 與橢圓
與橢圓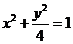 的交點為A、B,點
的交點為A、B,點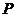 為橢圓上的動點,則使
為橢圓上的動點,則使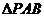 的面積為
的面積為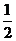 的點
的點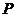 的個數為______.
的個數為______.
4.(2006江西)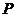 為雙曲線
為雙曲線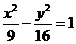 的右支上一點,
的右支上一點, 、
、 分別是圓
分別是圓
 上的點,則
上的點,則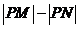 的最大值為( )
的最大值為( )
A.6 B.7 C.8 D.9
3.(2006江蘇)已知兩點M(-2,0)、N(2,0),點P為坐標平面內的動點,滿足 =0,則動點P(x,y)的軌跡方程為( )
=0,則動點P(x,y)的軌跡方程為( )
(A)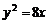 (B)
(B)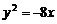 (C)
(C) (D)
(D)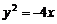
2.已知雙曲線的兩個焦點是橢圓 的兩個頂點,雙曲線的兩條準線經過橢圓的兩個焦點,則此雙曲線的方程是 ( )
的兩個頂點,雙曲線的兩條準線經過橢圓的兩個焦點,則此雙曲線的方程是 ( )
A.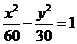 B.
B.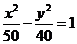 C.
C.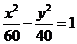 D.
D.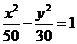
1.(2005北京)設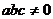 ,“
,“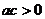 ”是“曲線
”是“曲線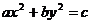 為橢圓”的( )
為橢圓”的( )
A.充分非必要條件 B.必要非充分條件
C.充分必要條件 D.既非充分又非必要條件
解析幾何是以數來研究形的學科,就是數形結合的學科;解析法就是通過坐標、方程所反映的數量間的關系和特征,來研究圖形的幾何性質。
圓錐曲線的綜合問題包括:解析法的應用,數形結合的思想,與圓錐曲線有關的定值、最值等問題;有圓錐曲線科內綜合,還有與代數、三角、幾何、向量等學科間的綜合。
復習中應注意掌握解析幾何的常用方法,如求曲線方程的方法、研究位置關系的方法、求范圍與最值的方法等,通過問題的解決,進一步培養函數與方程、等價轉化、分類討論等數學思想。
4.了解圓錐曲線的初步應用,掌握處理圓錐曲線綜合問題的常用方法.
3.掌握拋物線的定義、標準方程和拋物線的簡單幾何性質
2.掌握雙曲線的定義、標準方程和雙曲線的簡單幾何性質
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com