
4. (CUA)∩( CU B) = CU(A∪B) , (CUA)∪( CUB) = CU(A∩B);
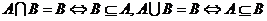 ,
,
對于含有n個元素的有限集合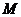 , 其子集、真子集、非空子集、非空真子集的個數依次為
, 其子集、真子集、非空子集、非空真子集的個數依次為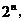
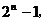
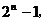
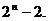 如滿足條件
如滿足條件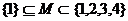 的集合
的集合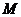 共有多少個?(特別注意
共有多少個?(特別注意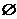 )
)
3.
集合 A、B,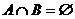 時,你是否注意到“極端”情況:
時,你是否注意到“極端”情況: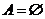 或
或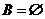 ;求集合的子集
;求集合的子集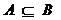 時是否忘記
時是否忘記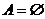 .
.
例如: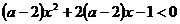 對一切
對一切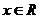 恒成立,求a的取植范圍,你討論了
恒成立,求a的取植范圍,你討論了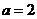 的情況了嗎?
的情況了嗎?
2. 研究集合,首先必須弄清代表元素,才能理解集合的意義.
(1)已知“集合M={y|y=x2 ,x∈R},N={y|y=x2+1,x∈R},求M∩N”;與“集合M={(x,y)|y=x2 ,x∈R},N={(x,y)|y=x2+1,x∈R}求M∩N”的區別.
(2)已知集合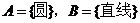 ,則
,則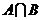 中的元素個數是____個.你注意空集了嗎?
中的元素個數是____個.你注意空集了嗎?
(3)設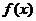 的定義域A是無限集,則下列集合中必為無限集的有
的定義域A是無限集,則下列集合中必為無限集的有
①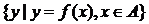 ②
②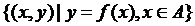
③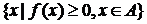 ④
④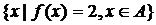
⑤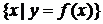
1. 研究集合必須注意集合元素的特征即三性(確定,互異,無序); 已知集合A={x,xy,lgxy},集合B={0,|x|,y},且A=B,則x+y=
14.二次方程、二次不等式、二次函數間的聯系你了解了嗎?二次方程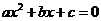 的兩個根即為二次不等式
的兩個根即為二次不等式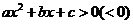 的解集的端點值,也是二次函數
的解集的端點值,也是二次函數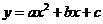 的圖象與
的圖象與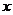 軸的交點的橫坐標。如(1)不等式
軸的交點的橫坐標。如(1)不等式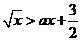 的解集是
的解集是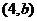 ,則
,則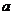 =__________(答:
=__________(答: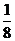 );(2)若關于
);(2)若關于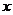 的不等式
的不等式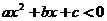 的解集為
的解集為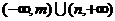 ,其中
,其中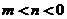 ,則關于
,則關于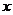 的不等式
的不等式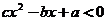 的解集為________(答:
的解集為________(答: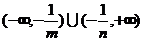 );(3)不等式
);(3)不等式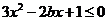 對
對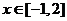 恒成立,則實數
恒成立,則實數 的取值范圍是_______(答:
的取值范圍是_______(答: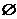 )。
)。
13.一元二次方程根的分布理論。方程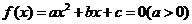 在
在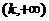 上有兩根、在
上有兩根、在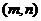 上有兩根、在
上有兩根、在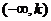 和
和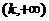 上各有一根的充要條件分別是什么?
上各有一根的充要條件分別是什么?
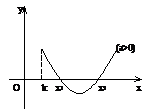 (
(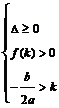 、
、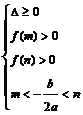 、
、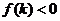 )。根的分布理論成立的前提是開區間,若在閉區間
)。根的分布理論成立的前提是開區間,若在閉區間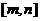 討論方程
討論方程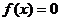 有實數解的情況,可先利用在開區間
有實數解的情況,可先利用在開區間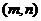 上實根分布的情況,得出結果,再令
上實根分布的情況,得出結果,再令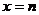 和
和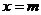 檢查端點的情況.如實系數方程
檢查端點的情況.如實系數方程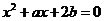 的一根大于0且小于1,另一根大于1且小于2,則
的一根大于0且小于1,另一根大于1且小于2,則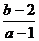 的取值范圍是_________(答:(
的取值范圍是_________(答:(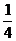 ,1))
,1))
12. 對于方程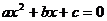 有實數解的問題。首先要討論最高次項系數
有實數解的問題。首先要討論最高次項系數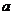 是否為0,其次若
是否為0,其次若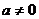 ,則一定有
,則一定有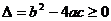 。對于多項式方程、不等式、函數的最高次項中含有參數時,你是否注意到同樣的情形?如:(1)
。對于多項式方程、不等式、函數的最高次項中含有參數時,你是否注意到同樣的情形?如:(1)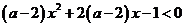 對一切
對一切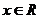 恒成立,則
恒成立,則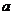 的取值范圍是_______(答:
的取值范圍是_______(答: );(2)關于
);(2)關于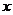 的方程
的方程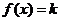 有解的條件是什么?(答:
有解的條件是什么?(答: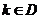 ,其中
,其中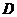 為
為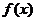 的值域),特別地,若在
的值域),特別地,若在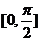 內有兩個不等的實根滿足等式
內有兩個不等的實根滿足等式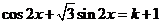 ,則實數
,則實數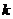 的范圍是_______.(答:
的范圍是_______.(答: )
)
11. 一元二次不等式的解集(聯系圖象)。尤其當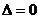 和
和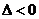 時的解集你會正確表示嗎?設
時的解集你會正確表示嗎?設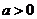 ,
,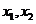 是方程
是方程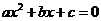 的兩實根,且
的兩實根,且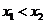 ,則其解集如下表:
,則其解集如下表:
|
|
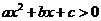 |
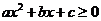 |
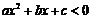 |
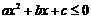 |
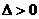 |
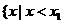 或 或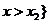 |
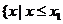 或 或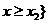 |
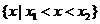 |
 |
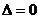 |
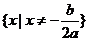 |
R |
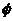 |
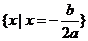 |
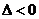 |
R |
R |
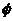 |
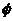 |
如解關于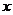 的不等式:
的不等式: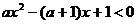 。(答:當
。(答:當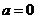 時,
時,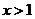 ;當
;當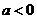 時,
時,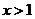 或
或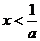 ;當
;當 時,
時,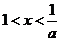 ;當
;當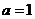 時,
時,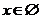 ;當
;當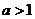 時,
時,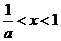 )
)
10. 一元一次不等式的解法:通過去分母、去括號、移項、合并同類項等步驟化為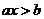 的形式,若
的形式,若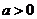 ,則
,則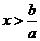 ;若
;若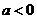 ,則
,則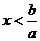 ;若
;若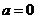 ,則當
,則當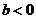 時,
時,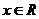 ;當
;當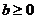 時,
時,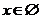 。如已知關于
。如已知關于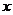 的不等式
的不等式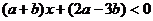 的解集為
的解集為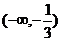 ,則關于
,則關于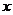 的不等式
的不等式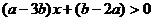 的解集為_______(答:
的解集為_______(答: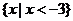 )
)
9.充要條件。關鍵是分清條件和結論(劃主謂賓),由條件可推出結論,條件是結論成立的充分條件;由結論可推出條件,則條件是結論成立的必要條件。從集合角度解釋,若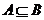 ,則A是B的充分條件;若
,則A是B的充分條件;若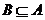 ,則A是B的必要條件;若A=B,則A是B的充要條件。如(1)給出下列命題:①實數
,則A是B的必要條件;若A=B,則A是B的充要條件。如(1)給出下列命題:①實數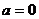 是直線
是直線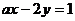 與
與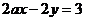 平行的充要條件;②若
平行的充要條件;②若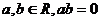 是
是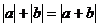 成立的充要條件;③已知
成立的充要條件;③已知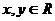 ,“若
,“若 ,則
,則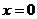 或
或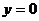 ”的逆否命題是“若
”的逆否命題是“若 或
或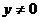 則
則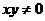 ”;④“若
”;④“若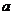 和
和 都是偶數,則
都是偶數,則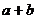 是偶數”的否命題是假命題 。其中正確命題的序號是_______(答:①④);(2)設命題p:
是偶數”的否命題是假命題 。其中正確命題的序號是_______(答:①④);(2)設命題p: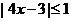 ;命題q:
;命題q: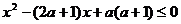 。若┐p是┐q的必要而不充分的條件,則實數a的取值范圍是
(答:
。若┐p是┐q的必要而不充分的條件,則實數a的取值范圍是
(答: )
)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com