
6.幾個重要結論:(1)已知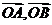 不共線,
不共線,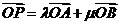 ,則A,P,B三點共線的充要條件是
,則A,P,B三點共線的充要條件是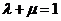 ;(2)向量中點公式:若C是AB的中點,則
;(2)向量中點公式:若C是AB的中點,則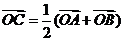 ;(3)向量重心公式:在
;(3)向量重心公式:在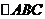 中,
中,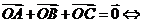
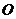 是
是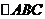 的重心.
的重心.
例:設F為拋物線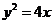 的焦點,A,B,C為該拋物線上三點,若
的焦點,A,B,C為該拋物線上三點,若 ,則
,則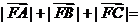 __________.
__________.
5.你還記得向量基本定理的幾何意義嗎?它的實質就是平面內的任何向量都可以用平面內任意不共線的兩個向量線性表示,它的系數的含義與求法你清楚嗎?
4.向量的運算要和實數運算有區別:(1)如兩邊不能約去一個向量,即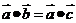 推不出
推不出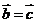 ,(2)向量的乘法不滿足結合律,即
,(2)向量的乘法不滿足結合律,即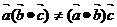 ,(3)兩向量不能相除.
,(3)兩向量不能相除.
3.利用向量平行或垂直來解決解析幾何中的平行和垂直問題可以不用討論斜率不存在的情況,要注意:
(1)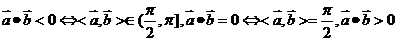
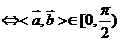
(2)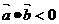 是向量
是向量 夾角為鈍角的必要而非充分條件.
夾角為鈍角的必要而非充分條件.
2.向量可以解決有關夾角、距離、平行和垂直等問題,要記住以下公式:|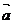 |2=
|2=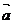 ·
·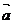 ,
,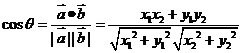
1.兩向量平行或共線的條件,它們兩種形式表示,你還記得嗎?注意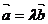 是向量平行的充分不必要條件.(定義及坐標表示)
是向量平行的充分不必要條件.(定義及坐標表示)
10、對于不等式恒成立問題,常用的處理方式?(轉化為最值問題)
9、解含參數的不等式的通法是“定義域為前提,函數增減性為基礎,分類討論是關鍵.”
8、 在解含有參數的不等式時,怎樣進行討論?(特別是指數和對數的底
在解含有參數的不等式時,怎樣進行討論?(特別是指數和對數的底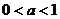 或
或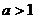 )討論完之后,要寫出:綜上所述,原不等式的解集是…….
)討論完之后,要寫出:綜上所述,原不等式的解集是…….
7、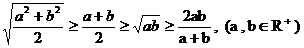 (當且僅當
(當且僅當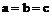 時,取等號); a、b、c
時,取等號); a、b、c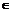 R,
R,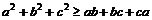 (當且僅當
(當且僅當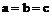 時,取等號);
時,取等號);
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com