
5.獨立性檢驗
(1)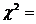 ,
,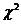 越大說明X與Y
越大說明X與Y
(2)獨立性檢驗的步驟
①假設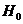
②計算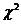
③與臨界值比較
④作出推斷
4.回歸分析:
(1)相關系數
r具有如下性質: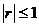 ,并且
,并且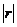 越接近于1,線性相關程度越
越接近于1,線性相關程度越 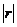 越接近于0,線性相關程度越
越接近于0,線性相關程度越
(2)相關性檢驗步驟
①提出統計假設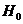 :變量
:變量 不具有相關關系;
不具有相關關系;
②計算出r的值;
③與臨界值 比較(
比較( 根據95%的要求與n-2查表可得);
根據95%的要求與n-2查表可得);
④作出統計推斷:如果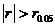 表明
表明
如果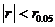 表明
表明
3.線性回歸方程:
 步驟:(1)由散點圖初步判定是否線性相關;
步驟:(1)由散點圖初步判定是否線性相關;
(2)列表求值;
(3)代入計算;
(4)交代結論
2.樣本估計總體中:注意頻率分布直方圖的縱坐標常為頻率/組距,小長方形的面積為其頻率.總體特征數的估計:
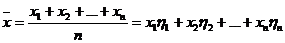 (
(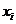 表示各組的組中值,
表示各組的組中值, 表示各組的頻率)
表示各組的頻率)
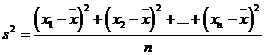
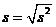
1.抽樣方法主要有簡單隨機抽樣(抽簽法、隨機數表法)常常用于總體數目較少時,主要特征是從總體中逐個抽取;系統抽樣,常用于總體個數較多時,主要特征是均衡分成若干部分,每部分只取一個;分層抽樣,主要特征是分層按比例抽樣,主要使用于總體中有明顯差異。它們的共同特征是每個個體被抽到的概率相等。
2.已知在矩形ABCD中,AB=5,AC=7,在矩形內任取一點P,求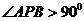 的概率.
的概率.
3.概率題的解題步驟:
(1)記事件
(2)交代總共結果數與A事件中結果數(幾何概率即D,d )
(3)計算
(4)作答
例如.1、在等腰直角三角形ABC中,
(1)在斜邊AB上任取一點M,求AM小于AC的概率;
(2)過頂點C在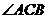 內任作一條射線CM,與線段AB交于點M,求
內任作一條射線CM,與線段AB交于點M,求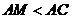 的概率.
的概率.
2.有關某個事件概率的求法:把所求的事件轉化為等可能事件的概率,轉化為若干個互斥事件中有一個發生的概率,利用對立事件的概率.
(1)若A、B互斥,則P(A+B)=P(A)+P(B);
(2)若A、B對立,則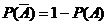 .
.
1.古典概型和幾何概型的區別.
例如:(1)任意取實數x [1,100],恰好落在[50,100]之間的概率為
[1,100],恰好落在[50,100]之間的概率為
(2)任意取整數x [1,100],恰好落在[50,100]之間的概率為
[1,100],恰好落在[50,100]之間的概率為
9.利用導數判斷方程的解的情況.
.已知函數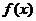 在
在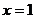 處的導數為1,則當
處的導數為1,則當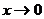 時
時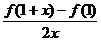 趨近于
趨近于
解析:由定義得當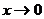 時,
時,
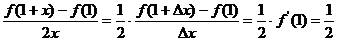
易錯原因:不會利用導數的定義來解題.
例2.函數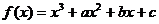 ,其中
,其中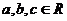 ,當
,當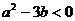 時,
時,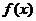 在R上的增減性是
在R上的增減性是
解析: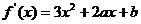 ,則
,則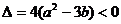 在R上
在R上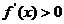 ,故是增函數.
,故是增函數.
易錯原因:不善于利用導函數的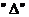 來判別單調性.
來判別單調性.
例3.若函數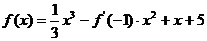 ,則
,則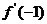 =
=
解析:設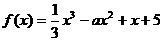 ,則
,則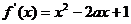 .故
.故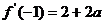 .由
.由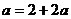 知
知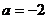 .有
.有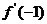 =-2.
=-2.
易錯原因:不會運用待定系數法解題.
例4.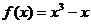 ,則當
,則當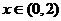 時,
時,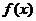 的值域為
的值域為
解析: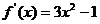 ,令
,令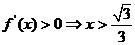 ,
,
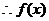 在區間
在區間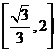 上單調增,在區間
上單調增,在區間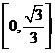 上單調減,
上單調減,

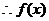 的值域為
的值域為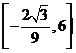 .
.
易錯原因:求導之后判別單調區間時概念模糊.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com