
12.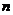 個互斥事件分別發生的概率的和P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An).
個互斥事件分別發生的概率的和P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An).
例題:. 由經驗得,在某超市的付款處排隊等候付款的人數及其概率如下:
|
排隊人數 |
0 |
1 |
2 |
3 |
4 |
5人以上 |
|
概
率 |
0.1 |
0.16 |
0.3 |
0.3 |
0.1 |
0.04 |
求:(1)至多有2個人排隊的概率;
(2)至少有2人排隊的概率.
解析:(1)設沒有人排除為事件A,1個人排隊為事件B,2個人排隊為事件C,則P(A)=0.1, P(B)=0.16, P(C)=0.3,依題意A、B、C彼此互斥,所以至多2個人排隊的概率為:
 P(A+B+C)=P(A)+P(B)+P(C)=0.1+0.16+0.3=0.56.
P(A+B+C)=P(A)+P(B)+P(C)=0.1+0.16+0.3=0.56.
(2)設至少2個人排隊為事件D,則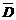 為至多1個人排隊,即
為至多1個人排隊,即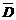 =A+B,因此
=A+B,因此
P(D)=1-P(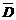 )=1-P(A+B)=1-[P(A)+P(B)]=1-(0.1+0.16)=0.74.
)=1-P(A+B)=1-[P(A)+P(B)]=1-(0.1+0.16)=0.74.
11.互斥事件A,B分別發生的概率的和P(A+B)=P(A)+P(B).
10.等可能性事件的概率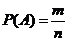 .
.
9.二項式定理 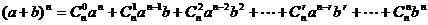 ;
;
二項展開式的通項公式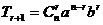
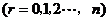 .
.
例題:函數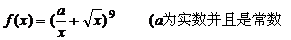 )
)
 (1)已知
(1)已知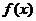 的展開式中
的展開式中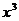 的系數為
的系數為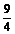 ,求常數
,求常數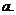
(2)是否存在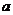 的值,使
的值,使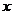 在定義域中取任意值時,
在定義域中取任意值時,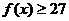 恒成立?如存在,求出
恒成立?如存在,求出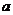 的值,如不存在,說明理由.
的值,如不存在,說明理由.
解析(1)Tr+1=C 由
由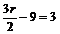 解得
解得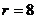
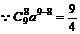
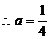
(2)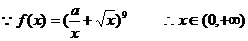 要使(
要使(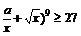
只需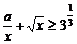
10當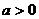 時,設
時,設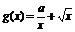
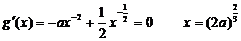
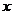 |
(0,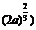 |
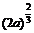 |
(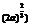 ,+ ,+ ) ) |
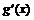 |
- |
0 |
+ |
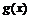 |
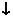 |
極小值 |
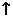 |
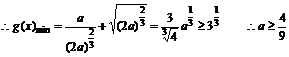
20當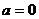 時,不成立 30當
時,不成立 30當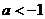 時,不成立 故當
時,不成立 故當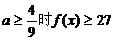
另解法 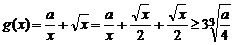 只需
只需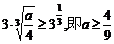
8.排列數與組合數的關系: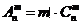 .
.
7.組合恒等式
(1)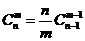 ; (2)
; (2)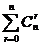 =
=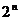 ; (3)
; (3)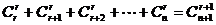 ;
;
(4)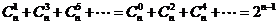
6.組合數的兩個性質
(1)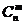 =
=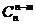 ;(2)
;(2) 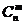 +
+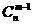 =
= ;注:規定
;注:規定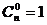 .
.
5.組合數公式
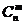 =
=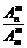 =
=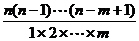 =
=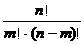 (
(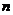 ∈N*,
∈N*,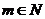 ,且
,且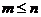 ).
).
4.排列恒等式
(1)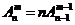 ;(2)
;(2) ;(3)
;(3)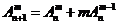 ;
;
(4) 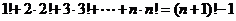 .
.
3.排列數公式
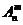 =
=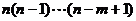 =
=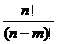 .(
.(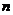 ,
,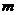 ∈N*,且
∈N*,且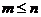 ).注:規定
).注:規定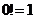 .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com