
2.分步計數原理(乘法原理)
 .
.
1.分類加法原理(加法原理)
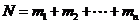 .
.
21.你注意到了嗎?求軌跡與求軌跡方程有區別的.求軌跡方程可別忘了尋求范圍呀!
(1) 是橢圓
是橢圓 的一個焦點,M在橢圓上,若
的一個焦點,M在橢圓上,若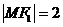 ,N是線段
,N是線段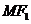 的中點,則|ON|的長度是(O是原點)
的中點,則|ON|的長度是(O是原點)
解析:考慮橢圓的定義,利用三角形的中位線,|ON|=4
易錯原因:找不到快速解題的思路,對于三角形的中位線應用不熟練.
(2)已知過橢圓的左焦點F且傾斜角為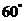 的直線交橢圓于A、B兩點,若|FA|=2|FB|,則橢圓離心率為
的直線交橢圓于A、B兩點,若|FA|=2|FB|,則橢圓離心率為
解析:作圖,過B作AC的垂線,垂足為E,可知E為AC的中點.
 ,故
,故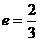 .
.
易錯原因:應用定義解題不夠熟練,構造三角形ABE有困難.
(3)若點P是以 、
、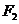 為焦點的橢圓
為焦點的橢圓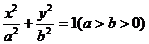 上的一點,且
上的一點,且 ,則橢圓離心率為
,則橢圓離心率為
解析: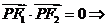
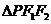 為直角三角形.
為直角三角形.
又 ,則
,則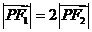 ,設
,設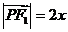 ,則
,則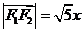
故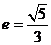 .
.
易錯原因:①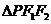 為直角三角形;②
為直角三角形;② 未用好.
未用好.
(4)已知點 、
、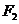 為橢圓
為橢圓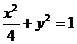 的焦點,若P為橢圓上的點,當
的焦點,若P為橢圓上的點,當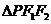 的面積為1時,
的面積為1時, 的值為
的值為
 解析:猜想
解析:猜想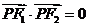 ,然后驗證此時
,然后驗證此時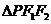 的面積為1,這種考慮抓住了填空題的特殊性,若設
的面積為1,這種考慮抓住了填空題的特殊性,若設 ,由點到直線的距離公式求
,由點到直線的距離公式求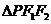 的高,同樣可以完成解答.
的高,同樣可以完成解答.
易錯原因:找不到解題的捷徑.
(5)已知橢圓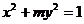 的焦點在
的焦點在 軸上,長軸長是短軸長的兩倍,那么
軸上,長軸長是短軸長的兩倍,那么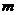 的值為
的值為
解析:將橢圓方程轉化為標準形式,注意焦點在 軸,故
軸,故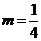
易錯原因:未考慮 的條件.
的條件.
附加題 ( 二項式定理,概率)
20.你知道嗎?解析幾何中解題關鍵就是把題目中的幾何條件代數化,特別是一些很不起眼的條件,有時起著關鍵的作用:如:點在曲線上、相交、共線、以某線段為直徑的圓經過某點、夾角、垂直、平行、中點、角平分線、中點弦問題等.圓和橢圓參數方程不要忘,有時在解決問題時很方便.數形結合是解決解幾問題的重要思想方法,要記得畫圖分析喲!
19.通徑是拋物線的所有焦點弦中最短的弦.
18.橢圓中,a,b,c的關系為----;離心率e=----;準線方程為----;焦點到相應準線距離為---- 雙曲線中,a,b,c的關系為----;離心率e=----;準線方程為----;焦點到相應準線距離為----
17. 在用圓錐曲線與直線聯立求解時,消元后得到的方程中要注意:二次項的系數是否為零?判別式
在用圓錐曲線與直線聯立求解時,消元后得到的方程中要注意:二次項的系數是否為零?判別式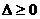 的限制.(求交點,弦長,中點,斜率,對稱,存在性問題都在
的限制.(求交點,弦長,中點,斜率,對稱,存在性問題都在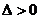 下進行).
下進行).
16.在利用圓錐曲線統一定義解題時,你是否注意到定義中的定比的分子分母的順序?兩個定義常常結伴而用,有時對我們解題有很大的幫助,有關過焦點弦問題用第二定義可能更為方便.(焦半徑公式:橢圓:|PF1|=---- ;|PF2|=---- ;雙曲線:|PF1|=---- ;|PF2|=---- (其中F1為左焦點F2為右焦點 );拋物線:|PF|=|x0|+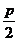 )
)
15.圓的切線的判定:①圓心到直線的距離等于圓的半徑;②經過半徑外端垂直于半徑的直線;③直線與圓的方程聯立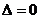 .
.
14.垂徑定理的幾種形式:①垂直于弦的直徑平分弦;②平分弦的直徑垂直于弦;③垂直平分弦的直線過圓心.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com