
20.解:(1)PB//平面EAC。 2分
(2)
正三角形PAD中,E為PD的中點,所以, ,
,
又 ,所以,AE⊥平面PCD。 6分
,所以,AE⊥平面PCD。 6分
 (3)在PC上取點M使得
(3)在PC上取點M使得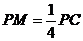 。
。
由于正三角形PAD及矩形ABCD,且AD=AB,所以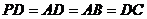
所以,在等腰直角三角形DPC中,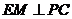 ,
,
連接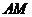 ,因為AE⊥平面PCD,所以,
,因為AE⊥平面PCD,所以,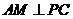 。
。
所以,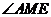 為二面角A-PC-D的平面角。
為二面角A-PC-D的平面角。
在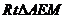 中,
中,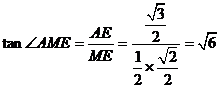 。
。
即二面角A-PC-D的正切值為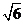 。 10分
。 10分
(4)設N為AD中點,連接PN,則 。
。
又面PAD⊥底面ABCD,所以,PN⊥底面ABCD。
所以,NB為PB在面ABCD上的射影。
 要使PB⊥AC,需且只需NB⊥AC
要使PB⊥AC,需且只需NB⊥AC
在矩形ABCD中,設AD=1,AB=x
則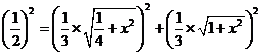 ,
,
解之得: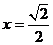 。
。
所以,當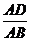
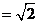 時,PB⊥AC。 14分
時,PB⊥AC。 14分
證法二:(按解法一相應步驟給分)
設N為AD中點,Q為BC中點,則因為 PAD是正三角形,底面ABCD是矩形,所以,
PAD是正三角形,底面ABCD是矩形,所以, ,
,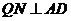 ,又因為側面PAD⊥底面ABCD,所以,
,又因為側面PAD⊥底面ABCD,所以,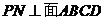 ,
,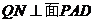 ,
,
以N為坐標原點,NA、NQ、NP所在直線分別為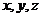 軸如圖建立空間直角坐標系。設
軸如圖建立空間直角坐標系。設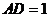 ,
, ,則
,則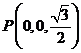 ,
,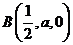 ,
,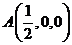 ,
,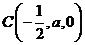 ,
,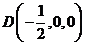 ,
,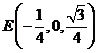 。
。
(2)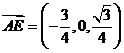 ,
, ,
,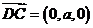 ,
,
 ,
,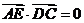
所以,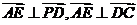 。
。
又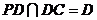 ,
,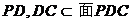 ,所以,AE⊥平面PCD。 6分
,所以,AE⊥平面PCD。 6分
(3)當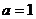 時,由(2)可知:
時,由(2)可知: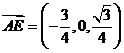 是平面PDC的法向量;
是平面PDC的法向量;
設平面PAC的法向量為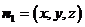 ,則
,則 ,
,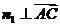 ,即
,即
 ,取
,取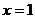 ,可得:
,可得: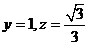 。所以,
。所以, 。
。
向量 與
與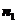 所成角
所成角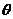 的余弦值為:
的余弦值為: 。
。
所以,tan q = 。
又由圖可知,二面角A-PC-D的平面角為銳角,所以,二面角A-PC-D的平面角就是向量 與
與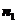 所成角
所成角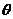 的補角。
的補角。
其正切值等于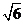 。 10分
。 10分
(4) ,
,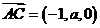 ,令
,令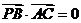 ,得
,得 ,所以,
,所以,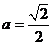 。所以,當
。所以,當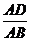
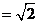 時,PB⊥AC。
時,PB⊥AC。
19.解:⑴由已知f′(x)=-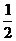 e-x(ax2+a+1)+
e-x(ax2+a+1)+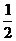 e-x·2ax
e-x·2ax
=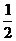 e-x(-ax2+2ax-a-1)
e-x(-ax2+2ax-a-1)
∴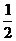 e-x>0,以下討論函數g(x)=-ax2+2ax-a-1
e-x>0,以下討論函數g(x)=-ax2+2ax-a-1
當a=0時,g(x)=-1<0,即f′(x)<0,∴f(x)是R上是減函數
當a>0時,g(x)=0的判斷式:△=4a2-4(a2+a)=-4a<0
∴g(x)<0即f′(x)<0, ∴f(x)在R上是減函數。
當a<0時,g(x)=0有兩個根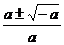 ,且
,且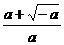 <
<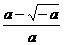
∴在(-∞,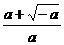 )上,g(x)>0,即f′(x)>0,f(x)在此區間上是增函數。
)上,g(x)>0,即f′(x)>0,f(x)在此區間上是增函數。
在(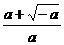 ,
,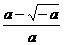 )上,g(x)<0,即f′(x)<0
)上,g(x)<0,即f′(x)<0
f(x)在區間上是減函數,在(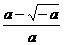 ,+∞)上,g(x)>0,即f′(x)>0
,+∞)上,g(x)>0,即f′(x)>0
f(x)在此區間上是增函數。
⑵當-1<a<0時,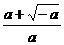 =1+
=1+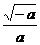 <1,
<1,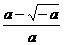 =1+
=1+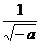 >2,∴在區間[1,2]上,函數f(x)單調遞減
>2,∴在區間[1,2]上,函數f(x)單調遞減
∴函數f(x)在[1,2]上的最小值為f(2)=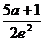
18.解:(1)
 |
3 |
4 |
5 |
6 |
|
P |
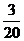 |
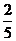 |
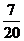 |
 |
(2)
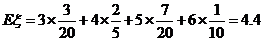
17.解:(1)∵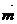 =(sinB,1-cosB)
, 且與向量
=(sinB,1-cosB)
, 且與向量 (2,0)所成角為
(2,0)所成角為
∴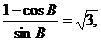 ∴tan
∴tan
(2)由(1)可得
 ’
’
∵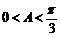 ∴
∴ ∴
∴ .
.
當且僅當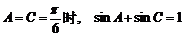
13. 11;1  4.
4. 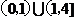 ;15.
;15. ; 16.①③
; 16.①③
22.(本題滿分14分)已知方向向量為 的直線l過點A(
的直線l過點A(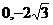 )和橢圓
)和橢圓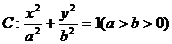 的焦點,
的焦點,
且橢圓C的中心O和橢圓的右準線上的點B滿足: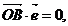 . |
. | |
|
(1)求橢圓C的方程;
(2)設M、N是橢圓C上兩個不同點,且M、N的縱坐標之和為1,記u為M、N的橫坐標之積.問是否存在最小的常數m ,
使u≤m恒成立?若存在,求出m的值;若不存在,說明理由.
|
本試卷分第Ⅰ卷和第Ⅱ卷兩部分,共150分,考試時間120分鐘
第Ⅰ卷(選擇題,共60分)
21.(本題滿分12分)設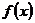 =
=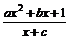 (a>0)為奇函數,且
(a>0)為奇函數,且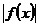 min=
min=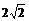 ,
,
數列{an}與{bn}滿足如下關系:a1=2, 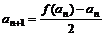 ,
,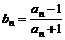 .
.
(1)求f(x)的解析表達式;
(2) 證明:當n∈N+時, 有bn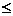
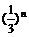 .
.
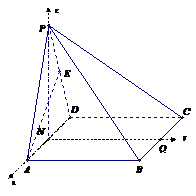
20. (本題滿分12分)如圖,四棱錐P -ABCD的底面是矩形,側面PAD是
正三角形,且側面PAD⊥底面ABCD,E 為側棱PD的中點。
(本題滿分12分)如圖,四棱錐P -ABCD的底面是矩形,側面PAD是
正三角形,且側面PAD⊥底面ABCD,E 為側棱PD的中點。
(1)試判斷直線PB與平面EAC的關系(不必證明);
(2)求證:AE⊥平面PCD;
(3)若AD = AB,試求二面角A-PC-D的正切值;
(4)當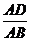 為何值時,PB⊥AC ?
為何值時,PB⊥AC ?
19.(本題滿分12分)設a∈R,函數f(x)=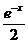 (ax2+a+1),其中e是自然對數的底數。
(ax2+a+1),其中e是自然對數的底數。
⑴判斷f(x)在R上的單調性;
⑵當-1<a<0時,求f(x)在[1,2]上的最小值。
18.(本題滿分12分).有甲、乙、丙、丁四支球隊進行單循環比賽,最后據各隊積分決出名次.規定每場比賽必須決出勝負,其中勝方積2分,負方積1分,已知球隊甲與球隊乙對陣,甲隊取勝的概率為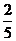 ,與球隊丙、丁對陣,甲隊取勝的概率均為
,與球隊丙、丁對陣,甲隊取勝的概率均為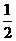 ,且各場次勝負情況彼此沒有影響.
,且各場次勝負情況彼此沒有影響.
(1)甲隊至少勝一場的概率; (2)求球隊甲賽后積分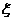 的概率分布和數學期望.
的概率分布和數學期望.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com