6．向心力
(1)作用：產(chǎn)生向心加速度，只改變線速度的方向，不改變速度的大小．因此，向心力對做圓周運動的物體不做功．
(2)大小： F＝ma＝mv2/r＝mω2 r=m4π2fr=m4π2r/T2=mωv
(3)方向：總是沿半徑指向圓心，時刻在變化．即向心力是個變力．
說明: 向心力是按效果命名的力，不是某種性質(zhì)的力，因此，向心力可以由某一個力提供，也可以由幾個力的合力提供，要根據(jù)物體受力的實際情況判定．
5．向心加速度
(1)物理意義：描述線速度方向改變的快慢
(2)大小：a=v2/r=ω2r=4π2fr=4π2r/T2=ωv，
(3)方向：總是指向圓心，方向時刻在變化．不論a的大小是否變化，a都是個變加速度．
(4)注意：a與r是成正比還是反比，要看前提條件，若ω相同，a與r成正比；若v相同，a與r成反比；若是r相同，a與ω2成正比，與v2也成正比．
4．V、ω、T、f的關(guān)系
T＝1/f，ω＝2π/T=2πf，v＝2πr/T＝2πrf=ωr．
T、f、ω三個量中任一個確定，其余兩個也就確定了．但v還和半徑r有關(guān)．
3．周期T，頻率f：做圓周運動物體一周所用的時間叫周期．
做圓周運動的物體單位時間內(nèi)沿圓周繞圓心轉(zhuǎn)過的圈數(shù)，叫做頻率，也叫轉(zhuǎn)速．
2．角速度：做勻速圓周運動的物體，連接物體與圓心的半徑轉(zhuǎn)過的圓心角與所用的時間的比值。
(l)物理意義：描述質(zhì)點繞圓心轉(zhuǎn)動的快慢．
(2)大小：ω＝φ/t(rad／s)
1．線速度：做勻速圓周運動的物體所通過的弧長與所用的時間的比值。
(1)物理意義：描述質(zhì)點沿切線方向運動的快慢．
(2)方向：某點線速度方向沿圓弧該點切線方向．
(3)大小：V=S/t
說明:線速度是物體做圓周運動的即時速度
3、平拋運動的拓展(類平拋運動)
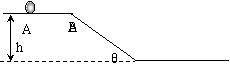
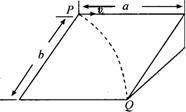[例7]如圖所示，光滑斜面長為a，寬為b，傾角為θ，一物塊沿斜面左上方頂點P水平射入，而從右下方頂點Q離開斜面，求入射初速度．
解析：物塊在垂直于斜面方向沒有運動，物塊沿斜面方向上的曲線運動可分解為水平方向上初速度v0的勻速直線運動和沿斜面向下初速度為零的勻加速運動．
在沿斜面方向上mgsinθ=ma加 a加＝gsinθ………①，水平方向上的位移s=a=v0t……②，沿斜面向下的位移y=b=½ a加t2……③，由①②③得v0＝a·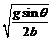
說明：運用運動分解的方法來解決曲線運動問題，就是分析好兩個分運動，根據(jù)分運動的運動性質(zhì)，選擇合適的運動學(xué)公式求解
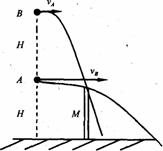[例8]從高H處的A點水平拋出一個物體，其水平射程為2s。若在A點正上方高H的B點拋出另一個物體，其水平射程為s。已知兩物體的運動軌跡在同一豎直平面內(nèi)，且都從同一豎屏M的頂端擦過，如圖所示，求屏M的高度h？
分析：思路1：平拋運動水平位移與兩個因素有關(guān)：初速大小和拋出高度，分別寫出水平位移公式，相比可得初速之比，設(shè)出屏M的頂端到各拋出點的高度，分別寫出與之相應(yīng)的豎直位移公式，將各自時間用水平位移和初速表示，解方程即可。
思路2：兩點水平拋出，軌跡均為拋物線，將“都從同一豎屏M的頂端擦過”轉(zhuǎn)化為數(shù)學(xué)條件：兩條拋物線均過同一點。按解析幾何方法求解。
解析:畫出各自軌跡示意圖
法一:由平拋運動規(guī)律根據(jù)題意得
2s=VAtA……①，s=VBtB……②，H=½gtA2……③, 2H=½gtB2……④
可得:
,又設(shè)各自經(jīng)過時間t1、t2從屏M的頂端擦過，則在豎直方向上有H－h(huán)=½gt12，2H－h(huán)=½gt22，在水平方向上有x=vAt1=vBt2，由以上三式解得h=6H/7。
法二：由平拋運動規(guī)律可得拋物線方程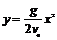
，依題意有yA=H－h(huán)，yB=2H－h(huán)時所對應(yīng)的x值相同，將(x，yA)(x，yB)分別代入各自的拋物線方程聯(lián)立求出h=6H/7。
[例9]排球場總長18m，網(wǎng)高2．25 m，如圖所示，設(shè)對方飛來一球，剛好在3m線正上方被我方運動員后排強(qiáng)攻擊回。假設(shè)排球被擊回的初速度方向是水平的，那么可認(rèn)為排球被擊回時做平拋運動。(g取10m/s2)
(1)若擊球的高度h＝2．5m，球擊回的水平速度與底線垂直，球既不能觸網(wǎng)又不出底線，則球被擊回的水平速度在什么范圍內(nèi)？
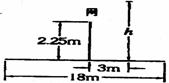(2)若運動員仍從3m線處起跳，起跳高度h滿足一定條件時，會出現(xiàn)無論球的水平初速多大都是觸網(wǎng)或越界，試求h滿足的條件。
[解析](1)球以vl速度被擊回，球正好落在底線上，則t1＝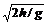
，vl=s/t1
將s=12m，h＝2．5m代入得v1=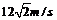
；
球以v2速度被擊回，球正好觸網(wǎng)，t2＝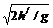
，v2=s//t2
將h/=(2.5－2.25)m＝0．25m，s/＝3m代入得v2=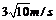
。故球被擊目的速度范圍是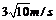＜v≤。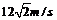
(2)若h較小，如果擊球速度大，會出界，如果擊球速度小則會融網(wǎng)，臨界情況是球剛好從球網(wǎng)上過去，落地時又剛好壓底線，則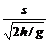
=
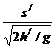，s、s/的數(shù)值同(1)中的值，h/＝
h－2．25(m)，由此得 h＝2.4m
故若h＜2.4m，無論擊球的速度多大，球總是觸網(wǎng)或出界。
試題展示
勻速圓周運動
知識簡析一、描述圓周運動的物理量
2、平拋運動的速度變化和重要推論
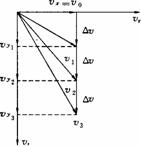
①水平方向分速度保持vx=v0.豎直方向，加速度恒為g,速度vy =gt,從拋出點起，每隔Δt時間的速度的矢量關(guān)系如圖所示．這一矢量關(guān)系有兩個特點：(1)任意時刻的速度水平分量均等于初速度v0; (2)任意相等時間間隔Δt內(nèi)的速度改變量均豎直向下，且Δv=Δvy=gΔt.
②平拋物體任意時刻瞬時時速度方向的反向延長線與初速度延長線的交點到拋出點的距離都等于水平位移的一半。
證明：設(shè)時間t內(nèi)物體的水平位移為s，豎直位移為h，則末速度的水平分量vx=v0=s/t，而豎直分量vy=2h/t，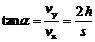 
， 所以有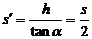
[例5]作平拋運動的物體，在落地前的最后1s內(nèi)，其速度方向由跟豎直方向成600角變?yōu)楦Q直方向成450角，求:物體拋出時的速度和高度分別是多少？
解析一:設(shè)平拋運動的初速度為v0，運動時間為t，則經(jīng)過(t一1)s時vy＝g(t一1)，
tan300＝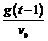
經(jīng)過ts時：vy＝gt，tan450＝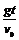
,∴
,
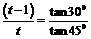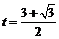
V0=gt/tan450＝23.2 m/s.H＝½gt2＝27. 5 m.
解析二：此題如果用結(jié)論解題更簡單．
ΔV＝gΔt=9. 8m/s.又有V0cot450一v0cot600=ΔV，解得V0=23. 2 m/s，
H=vy2/2g＝27. 5 m.
說明:此題如果畫出最后1s初、末速度的矢量圖，做起來更直觀．
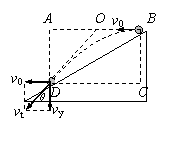
[例6] 從傾角為θ=30°的斜面頂端以初動能E=6J向下坡方向平拋出一個小球，則小球落到斜面上時的動能E /為______J。
解：以拋出點和落地點連線為對角線畫出矩形ABCD，可以證明末速度vt的反向延長線必然交AB于其中點O，由圖中可知AD∶AO=2∶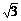
，由相似形可知vt∶v0=
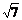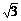∶，因此很容易可以得出結(jié)論：E /=14J。
2、處理平拋物體的運動時應(yīng)注意：
① 水平方向和豎直方向的兩個分運動是相互獨立的，其中每個分運動都不會因另一個分運動的存在而受到影響--即垂直不相干關(guān)系；
② 水平方向和豎直方向的兩個分運動具有等時性，運動時間由高度決定，與v0無關(guān)；
③ 末速度和水平方向的夾角不等于位移和水平方向的夾角，由上證明可知tgβ=2tgα
[例1] 物塊從光滑曲面上的P點自由滑下，通過粗糙的靜止水平傳送帶以后落到地面上的Q點，若傳送帶的皮帶輪沿逆時針方向轉(zhuǎn)動起來，使傳送帶隨之運動，如圖1－16所示，再把物塊放到P點自由滑下則
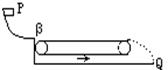A.物塊將仍落在Q點
B.物塊將會落在Q點的左邊
C.物塊將會落在Q點的右邊
D.物塊有可能落不到地面上
解答:物塊從斜面滑下來，當(dāng)傳送帶靜止時，在水平方向受到與運動方向相反的摩擦力，物塊將做勻減速運動。離開傳送帶時做平拋運動。當(dāng)傳送帶逆時針轉(zhuǎn)動時物體相對傳送帶都是向前運動，受到滑動摩擦力方向與運動方向相反。 物體做勻減速運動，離開傳送帶時，也做平拋運動，且與傳送帶不動時的拋出速度相同，故落在Q點，所以A選項正確。
[小結(jié)]若此題中傳送帶順時針轉(zhuǎn)動，物塊相對傳送帶的運動情況就應(yīng)討論了。
(1)當(dāng)v0=vB物塊滑到底的速度等于傳送帶速度，沒有摩擦力作用，物塊做勻速運動，離開傳送帶做平拋的初速度比傳送帶不動時的大，水平位移也大，所以落在Q點的右邊。
(2)當(dāng)v0＞vB物塊滑到底速度小于傳送帶的速度，有兩種情況，一是物塊始終做勻加速運動，二是物塊先做加速運動，當(dāng)物塊速度等于傳送帶的速度時，物體做勻速運動。這兩種情況落點都在Q點右邊。
(3)v0＜vB當(dāng)物塊滑上傳送帶的速度大于傳送帶的速度，有兩種情況，一是物塊一直減速，二是先減速后勻速。第一種落在Q點，第二種落在Q點的右邊。
規(guī)律方法 1、平拋運動的分析方法
用運動合成和分解方法研究平拋運動，要根據(jù)運動的獨立性理解平拋運動的兩分運動，即水平方向的勻速直線運動和豎直方向的自由落體運動．其運動規(guī)律有兩部分：一部分是速度規(guī)律，一部分是位移規(guī)律．對具體的平拋運動，關(guān)鍵是分析出問題中是與位移規(guī)律有關(guān)還是與速度規(guī)律有關(guān)
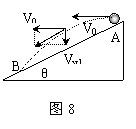[例2]如圖在傾角為θ的斜面頂端A處以速度V0水平拋出一小球，落在斜面上的某一點B處，設(shè)空氣阻力不計，求(1)小球從A運動到B處所需的時間；(2)從拋出開始計時，經(jīng)過多長時間小球離斜面的距離達(dá)到最大？
解析：(1)小球做平拋運動，同時受到斜面體的限制，設(shè)從小球從A運動到B處所需的時間為t,則：水平位移為x=V0t
豎直位移為y=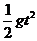
, 由數(shù)學(xué)關(guān)系得到: 
(2)從拋出開始計時，經(jīng)過t1時間小球離斜面的距離達(dá)到最大,當(dāng)小球的速度與斜面平行時，小球離斜面的距離達(dá)到最大。因Vy1=gt1=V0tanθ,所以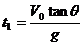
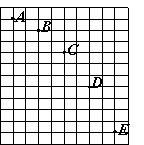
[例3] 已知方格邊長a和閃光照相的頻閃間隔T，求：v0、g、vc
解：水平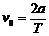方向：
豎直方向：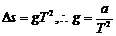
先求C點的水平分速度vx和豎直分速度vy，再求合速度vC：
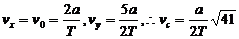
[例4]如圖所示，一高度為h=0.2m的水平面在A點處與一傾角為θ=30°的斜面連接，一小球以V0=5m/s的速度在平面上向右運動。求小球從A點運動到地面所需的時間(平面與斜面均光滑，取g=10m/s2)。某同學(xué)對此題的解法為：小球沿斜面運動，則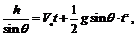
由此可求得落地的時間t。問：你同意上述解法嗎？若同意，求出所需的時間；若不同意，則說明理由并求出你認(rèn)為正確的結(jié)果。
解析：不同意。小球應(yīng)在A點離開平面做平拋運動，而不是沿斜面下滑。
正確做法為：落地點與A點的水平距離
斜面底寬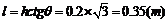 
因為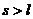
,所以小球離開A點后不會落到斜面，因此落地時間即為平拋運動時間。
∴ 
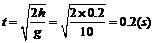
1、平拋運動：將物體沿水平方向拋出，其運動為平拋運動．
(1)運動特點：a、只受重力；b、初速度與重力垂直．盡管其速度大小和方向時刻在改變，但其運動的加速度卻恒為重力加速度g，因而平拋運動是一個勻變速曲線運動
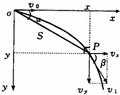(2)平拋運動的處理方法：平拋運動可分解為水平方向的勻速直線運動和豎直方向的自由落體運動。水平方向和豎直方向的兩個分運動既具有獨立性，又具有等時性．
(3)平拋運動的規(guī)律：以物體的出發(fā)點為原點，沿水平和豎直方向建成立坐標(biāo)。
ax=0……①
ay=0……④
水平方向 vx=v0 ……② 豎直方向 vy=gt……⑤
x=v0t……③ y=½gt2……⑥
①平拋物體在時間t內(nèi)的位移S可由③⑤兩式推得s=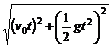
=
，
②位移的方向與水平方向的夾角α由下式?jīng)Q定tgα=y/x=½gt2/v0t=gt/2v0
③平拋物體經(jīng)時間t時的瞬時速度vt可由②⑤兩式推得vt=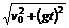
，
④速度vt的方向與水平方向的夾角β可由下式?jīng)Q定tgβ=vy/vx=gt/v0
⑤平拋物體的軌跡方程可由③⑥兩式通過消去時間t而推得：y=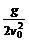
·x2， 可見，平拋物體運動的軌跡是一條拋物線．
⑥運動時間由高度決定，與v0無關(guān)，所以t=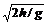，水平距離x＝v0t＝v0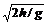
⑦Δt時間內(nèi)速度改變量相等，即△v＝gΔt，ΔV方向是豎直向下的．說明平拋運動是勻變速曲線運動．
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com