
綜上, 得到 a ∈ (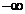 , -
, -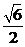 ]∪[1 ,
]∪[1 ,  ).
).
類似地, 也可以利用拋物線頂點的縱坐標討論. 如:
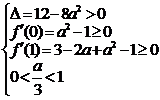 , 解得
, 解得 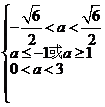 . 所以 a ∈[1,
. 所以 a ∈[1,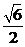 ).
).
(ii) 若Δ> 0, 為使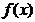 在 (
在 (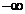 , 0 ) 和 ( 1,
, 0 ) 和 ( 1,  ) 為增函數, 只需
) 為增函數, 只需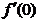 ≥0,
≥0,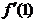 ≥0且0 <
≥0且0 <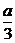 < 1. 由
< 1. 由
即
a∈(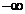 , -
, -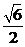 ]∪[1 ,
]∪[1 ,  ).
).
解法2 利用拋物線的對稱軸討論.
(i) 若Δ≤0, 這種情況的求解與解法1相同, 不再贅述.
綜上, a的取值范圍為 (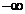 , -
, -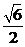 ]∪[
]∪[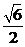 ,
,  )∪[1 ,
)∪[1 , 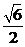 ).
).
由 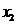 ≤1 得
≤1 得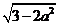 ≤3-a, 解得
-
≤3-a, 解得
-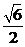 < a <
< a < 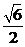 . 從而 a∈[1,
. 從而 a∈[1,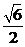 ).
).
由 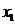 ≥0 得 a ≥
≥0 得 a ≥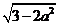 , 解得1 ≤ a <
, 解得1 ≤ a < 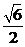 .
.
為使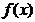 在(
在(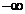 , 0 )和( 1,
, 0 )和( 1,  )為增函數, 必須
)為增函數, 必須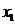 ≥0且
≥0且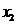 ≤1.
≤1.
當x∈(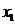 ,
,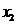 )時,
)時, 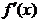 < 0,
< 0, 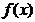 為減函數.
為減函數.
當x∈(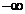 ,
,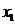 )或(
)或(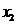 ,
, )時,
)時, 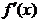 > 0,
> 0, 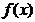 為增函數;
為增函數;
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com