日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

    若1< a <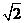, 則當y = －1時, | PQ | 取最大值2 .

    解法2:

    若a ≥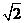, 則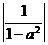≤1, 當y = 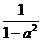時, | PQ | 取最大值;

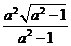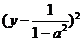
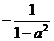       = (1)  + 1 + .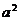

    因為 | y | ≤ 1, a > 1,

       = (1)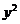－2y +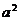 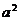1 +

 = (1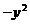) + 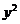－2y + 1

    又因為Q在橢圓上, 所以 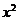 = 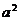(1) .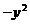

    解法1:  依題意可設 P (0, 1 ), Q (x , y ), 則| PQ | = .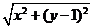

    [解答分析] 要求| PQ |的最大值, 為方便, 對加以討論. 首先需寫出點P、Q的坐標. 因Q在橢圓上, 通過消元法消去中的一個未知數(這里消x), 得到關于y的表達式, 是一個y的二次式, 配平方. 其中有參數a, 需結合此橢圓的性質分類討論, 從而求出| PQ |的最大值.

    本題屬于難題, 區分度較好. 六道解答題中, 本題不能入門得0分者最多, 達57%. 除此之外, 得分主要分布在1~6分. 僅寫出P、Q的坐標得1~2分者有約五分之一, 能寫出| PQ |的表達式并消元得5~6分者有7%, 進一步將的表達式配平方, 而未加討論寫出| PQ |的最大值得8~9分者有7%, 基本完成解答, 得10分及其以上者有3%, 得滿分者為1.3%.

    [考查意圖] 本題主要考查橢圓的基本知識、兩點間的距離及綜合分析問題的能力.

   0.13