
 ㈥數列應用
㈥數列應用
點評:本題以新名詞“絕對差數列”出現,考查學生構造新數列的能力;以及利用已知條件,通過觀察、歸納、證明的能力. 其中(Ⅱ)可說明數列 是周期數列,而
是周期數列,而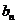 是常數列;(Ⅲ)要求學生有較深厚的數學功底,可考慮使用反證法與放縮法證明.
是常數列;(Ⅲ)要求學生有較深厚的數學功底,可考慮使用反證法與放縮法證明.
(Ⅱ)若“絕對差數列”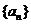 中,
中,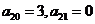 ,數列
,數列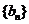 滿足
滿足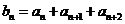 ,
,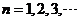 ,分別判斷當
,分別判斷當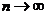 時,
時, 與
與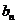 的極限是否存在,如果存在,求出其極限值;
的極限是否存在,如果存在,求出其極限值;
(Ⅲ)證明:任何“絕對差數列”中總含有無窮多個為零的項.
(2007年北京卷)在數列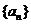 中,若
中,若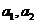 是正整數,且
是正整數,且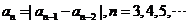 ,則稱
,則稱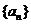 為“絕對差數列”.
為“絕對差數列”.
(Ⅰ)舉出一個前五項不為零的“絕對差數列”(只要求寫出前十項);
(3)若(2)中的數列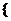
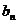
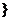 滿足不等式|
滿足不等式|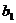 -
- |+|
|+|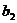 -
- |+┅+|
|+┅+|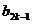 -
- |+|
|+|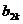 -
- |≤4,求
|≤4,求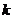 的值.
的值.
點評:本題主要考查等比數列的基本知識.
㈤新定義型數列
(2)若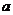 =2
=2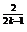 ,數列
,數列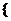
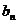
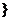 滿足
滿足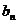 =
=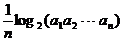 (
(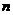 =1,2,┅,2
=1,2,┅,2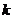 ),求數列
),求數列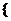
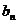
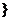 的通項公式;
的通項公式;
(1)求證:數列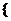

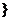 是等比數列;
是等比數列;
(2007年上海卷)已知有窮數列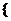

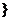 共有2
共有2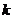 項(整數
項(整數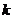 ≥2),首項
≥2),首項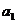 =2.設該數列的前
=2.設該數列的前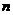 項和為
項和為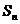 ,且
,且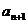 =
=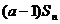 +2(
+2(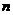 =1,2,┅,2
=1,2,┅,2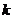 -1),其中常數
-1),其中常數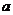 >1.
>1.
點評:此題主要考查怎樣用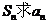 ,注意分兩步進行.
,注意分兩步進行.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com