
1.(2007年江西卷)某商場舉行抽獎促銷活動,抽獎規則是:從裝有9個白球,1個紅球的箱子中每次隨機地摸出一個球,記下顏色后放回,摸出一個紅球可獲得獎金10元;摸出2個紅球可獲得獎金50元,現有甲,乙兩位顧客,規定:甲摸一次,乙摸兩次,令x表示甲,乙摸球后獲得的獎金總額.求:
(1)x的分布列; (2)x的的數學期望.
6.(2007年四川卷)某課程考核分理論與實驗兩部分進行,每部分考核成績只記“合格”與“不合格”,兩部分考核都是“合格”則該課程考核“合格”,甲、乙、丙三人在理論考核中合格的概率分別為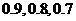 ;在實驗考核中合格的概率分別為
;在實驗考核中合格的概率分別為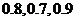 ,所有考核是否合格相互之間沒有影響,
,所有考核是否合格相互之間沒有影響,
(Ⅰ)求甲、乙、丙三人在理論考核中至少有兩人合格的概率;
(Ⅱ)求這三人該課程考核都合格的概率.(結果保留三位小數)
點評:本小題主要考察相互獨立事件、互斥事件、對立事件等概率的計算方法,考察應用概率知識解決實際問題的能力.滿分12分.
㈤分布列、期望、方差
假設某應聘者對三門指定課程考試及格的概率分別是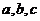 ,且三門課程考試是否及格相互之間沒有影響.
,且三門課程考試是否及格相互之間沒有影響.
(Ⅰ)分別求該應聘者用方案一和方案二時考試通過的概率;
(Ⅱ)試比較該應聘者在上述兩種方案下考試通過的概率的大小.(說明理由)
點評:本題考查相互獨立事件同時發生的概率以及利用作差比較法比較兩個值大小的變形能力.
5.(2007年北京卷)某公司招聘員工,指定三門考試課程,有兩種考試方案.
方案一:考試三門課程,至少有兩門及格為考試通過;
方案二:在三門課程中,隨機選取兩門,這兩門都及格為考試通過.
4.( 2007年湖南卷)某安全生產監督部門對5家小型煤礦進行安全檢查(簡稱安檢).若安檢不合格,則必須進行整改.若整改后經復查仍不合格,則強行關閉.設每家煤礦安檢是否合格是相互獨立的,且每家煤礦整改前安檢合格的概率是0.5, 整改后安檢合格的概率是0.8,計算(結果精確到0.01):
(Ⅰ)恰好有兩家煤礦必須整改的概率;
(Ⅱ)平均有多少家煤礦必須整改;
(Ⅲ)至少關閉一家煤礦的概率.
點評:本題考查概率中的二項分布,Pn(k)公式等,考查學生分析問題解決問題的能力.
(Ⅱ)若取到的4個球中至少有2個紅球的概率為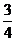 ,求n.
,求n.
點評:本題主要考查排列組合、概率等基本知識,同時考查邏輯思維能力和數學應用能力.
3.( 2007年浙江卷)甲、乙兩袋裝有大小相同的紅球和白球,甲袋裝有2個紅球,2個白球;乙袋裝有2個紅球,n個白球.從甲,乙兩袋中各任取2個球.
(Ⅰ)若n=3,求取到的4個球全是紅球的概率;
A.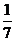 B.
B.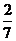 C.
C.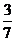 D.
D.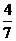
1.(2007年安徽卷)在正方體上任選3個頂點連成三角形,則所得的三角形是直角非等腰三角形的概率為( )
令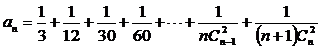 ,則
,則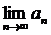 =__1/2__.
=__1/2__.
㈣概率:
等可能事件(選擇填空題) 對立事件、相互獨立事件、獨立重復事件(解答題綜合)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com