日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

③若直線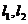與同一平面所成的角相等,則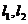互相平行.

[解]

點評:本題主要考查正余弦定理的應用.

高考啟示錄------立體幾何

縱觀2007年全國各省市高考試題，高考立體幾何試題一般共有3道(客觀題2道, 主觀題1道), 共計總分21分左右,考查的知識點在20個以內. 選擇填空題考核立幾中的計算型問題, 而解答題著重考查立幾中的邏輯推理型問題, 當然, 二者均應以正確的空間想象為前提. 隨著新的課程改革的進一步實施,立體幾何考題正朝著傳統方法和空間向量的方法相結合解決問題的方向發展.從歷年的考題變化看, 以多面體和球體為載體的線面位置關系的論證,角與距離的探求是常考常新的熱門話題. 向量的數量積常用于有關向量相等，兩向量垂直、射影、夾角等問題中.常用向量的直角坐標運算來證明向量的垂直和平行問題；利用向量的夾角公式和距離公式求解空間兩條直線的夾角和兩點間距離的問題.

（一）空間垂直與平行

例1（2007遼寧卷）給出下列四個命題:

    ①垂直于同一直線的兩條直線互相平行.

②垂直于同一平面的兩個平面互相平行.

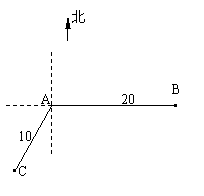
（2007年上海卷）如圖，當甲船位于A處時獲悉，在其正東方向相距20海里的B處有一艘漁船遇險等待營救．甲船立即前往救援，同時把消息告知在甲船的南偏西30，相距10海里C處的乙船，試問乙船應朝北偏東多少度的方向沿直線前往B處救援（角度精確到1）？

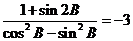（Ⅱ）若，求.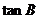

點評：本小題主要考查三角函數概念、同角三角函數的關系、兩角和與差的三角函數的公式以及倍角公式，考查應用、分析和計算能力.滿分12分.

㈥三角應用

（Ⅰ）求角；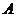

（2007年四川卷）已知是三角形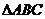三內角，向量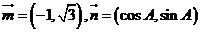，且.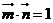

（1）       求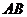的值；（2）求的值.

點評：旨在考查斜三角形中的正余弦定理和角的正弦公式，考查基本運算能力及分析和解決問題的能力.

㈤向量與三角

（2007年天津卷）如圖，在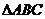中，，，．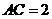

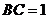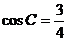       （II）函數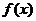的圖象可以由函數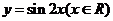的圖象經過怎樣的變換得到？

點評：本小題主要考查三角函數的基本公式、三角恒等變換、三角函數的圖象和性質等基本知識，以及推理和運算能力.滿分12分.

㈣三角形中的三角問題

       （I）求函數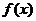的最小正周期和單調增區間；