
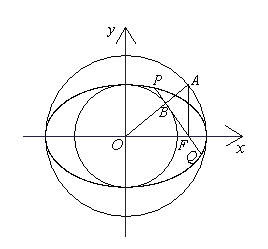
3.(2007年天津卷)如圖,以橢圓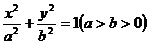 的中心
的中心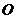 為圓心,分別以
為圓心,分別以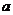 和
和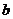 為半徑作大圓和小圓.過橢圓右焦點
為半徑作大圓和小圓.過橢圓右焦點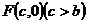 作垂直于
作垂直于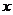 軸的直線交大圓于第一象限內的點
軸的直線交大圓于第一象限內的點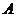 .連結
.連結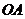 交小圓于點
交小圓于點 .設直線
.設直線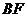 是小圓的切線.
是小圓的切線.
 點評:本小題主要考察雙曲線的定義和性質、直線與雙曲線的關系、點到直線的距離等知識及解析幾何的基本思想、方法和綜合解決問題的能力.滿分12分.
點評:本小題主要考察雙曲線的定義和性質、直線與雙曲線的關系、點到直線的距離等知識及解析幾何的基本思想、方法和綜合解決問題的能力.滿分12分.
2.(2007年四川卷)已知兩定點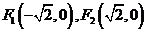 ,滿足條件
,滿足條件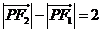 的點
的點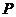 的軌跡是曲線
的軌跡是曲線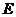 ,直線
,直線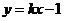 與曲線
與曲線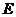 交于
交于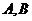 兩點,如果
兩點,如果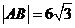 ,且曲線
,且曲線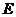 上存在點
上存在點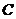 ,使
,使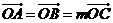 ,求
,求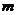 的值和
的值和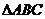 的面積
的面積 .
.
(2) 過點P(0,4)的直線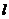 ,交雙曲線C于A,B兩點,交x軸于Q點(Q點與C的頂點不重合).當
,交雙曲線C于A,B兩點,交x軸于Q點(Q點與C的頂點不重合).當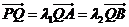 ,且
,且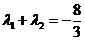 時,求Q點的坐標.
時,求Q點的坐標.
點評:本題主要考查橢圓與雙曲線的基本概念、標準方程、幾何性質等基礎知識和基本運算能力.
1.(2007年山東卷)雙曲線C與橢圓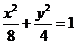 有相同的焦點,直線y=
有相同的焦點,直線y=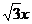 為C的一條漸近線.
為C的一條漸近線.
(1) 求雙曲線C的方程;
(Ⅱ)是否存在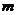 、
、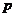 的值,使拋物線C2的焦點恰在直線AB上?若存在,求出符合條件的
的值,使拋物線C2的焦點恰在直線AB上?若存在,求出符合條件的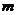 、
、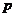 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
點評:本題主要考查直線與橢圓的位置關系,拋物線的定義等問題,考查學生計算、數形結合等方面綜合的能力.
㈥解析幾何與向量相結合:注意平面幾何知識的應用
(Ⅰ)當AB⊥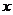 軸時,求
軸時,求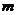 、
、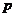 的值,并判斷拋物線C2的焦點是否在直線AB上;
的值,并判斷拋物線C2的焦點是否在直線AB上;
3.( 2007年湖南卷)已知橢圓C1: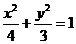 ,拋物線C2:
,拋物線C2: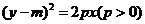 ,且C1、C2的公共弦AB過橢圓C1的右焦點.
,且C1、C2的公共弦AB過橢圓C1的右焦點.
(Ⅱ)若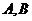 是
是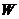 上的不同兩點,
上的不同兩點,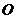 是坐標原點,求
是坐標原點,求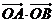 的最小值.
的最小值.
點評:考查雙曲線的定義,以及利用代數的方法―坐標法解決幾何問題,會轉化為函數的最值,又考查分類討論的思想和函數思想.
(Ⅰ)求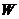 的方程;
的方程;
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com