
d=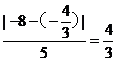 ,故選(A).
,故選(A).
法三:設(shè)直線方程為4x+3y+C=0則當(dāng)l與拋物線相切時(shí)l與4x+3y-8=0間的距離為所求最小,由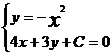 得4x-3x
得4x-3x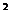 +C=0,∴△=16+
+C=0,∴△=16+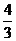 ,此時(shí)
,此時(shí)
法二:設(shè)拋物線上點(diǎn)P(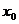 ,-
,-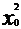 )到直線4x+3y-8=0距離最小,則過(guò)P且與拋物線相切的直線與4x+3y-8=0平行,故y
)到直線4x+3y-8=0距離最小,則過(guò)P且與拋物線相切的直線與4x+3y-8=0平行,故y (
( 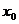 )=-2
)=-2 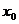 =-
=-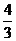 ,∴
,∴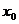 =
= ,∴P(
,∴P( ,-
,-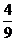 ),此時(shí)d=
),此時(shí)d=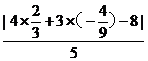 =
=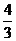 ,故選(A).
,故選(A).
[解答提示] 法一:設(shè)拋物線上任一點(diǎn)坐標(biāo)為P(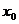 ,-
,-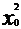 ),由點(diǎn)到直線的距離公式得P到直線的距離d(
),由點(diǎn)到直線的距離公式得P到直線的距離d(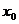 )=
)=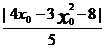 =
=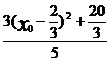
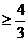 ,當(dāng)
,當(dāng)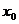 =
= 時(shí),d(
時(shí),d(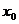 )取得最大值
)取得最大值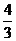 ,故選(A).
,故選(A).
(A)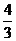 (B)
(B)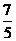 (C)
(C)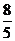 (D)
(D)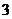
[答題情況]答案:(A)
[考查意圖] 本題主要考查直線與拋物線的位置關(guān)系,點(diǎn)到直線距離公式等基本知識(shí),考查數(shù)形結(jié)合和函數(shù)的思想與方法.
[錯(cuò)因分析] 幾何問(wèn)題代數(shù)化的思想與方程不熟悉及解析幾何中數(shù)與形的結(jié)合不明確是出錯(cuò)的重要原因.
文(11)理(8)拋物線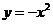 上的點(diǎn)到直線
上的點(diǎn)到直線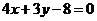 距離的最小值是( )
距離的最小值是( )
解法二:由圓的方程知圓心C(1,1),半徑r=1,設(shè)兩切線的夾角為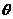 ,則
,則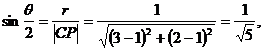
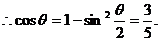 應(yīng)選(B).
應(yīng)選(B).
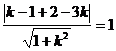 ,解之得: k=0或
,解之得: k=0或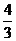 .設(shè)兩切線的夾角為
.設(shè)兩切線的夾角為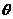 ,則
,則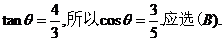 (注:本方法也可用判別式
(注:本方法也可用判別式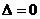 求斜率k.)
求斜率k.)
[解答提示] 解法一:圓的方程可化為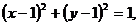 其圓心為(1,1),半徑r=1.設(shè)切線的斜率為k,則切線方程為y-2=k(x-3),即kx-y+2-3k=0.由圓心到切線的距離等于半徑r得:
其圓心為(1,1),半徑r=1.設(shè)切線的斜率為k,則切線方程為y-2=k(x-3),即kx-y+2-3k=0.由圓心到切線的距離等于半徑r得:
(A)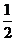 (B)
(B)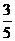 (C)
(C)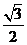 (D)
(D)
[答題情況]答案:(B)
[考查意圖] 本題主要考查直線與圓的位置關(guān)系以及直線夾角等基本知識(shí).
[錯(cuò)因分析] 圓的切線方程不會(huì)求或兩直線夾角公式記憶不清是出錯(cuò)的重要原因.
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com