日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

若，則　 　

(屆高三昆明一中模擬)設函數(shù)，若

是偶函數(shù)，則等于　　　　 　　　

(屆高三江蘇徐州模擬)設函數(shù)是奇函數(shù)，

則　　　　　　

若，，，則　

函數(shù)的單調(diào)遞減區(qū)間是　　　　　　　　 　　

①函數(shù)在它的定義域內(nèi)是增函數(shù)；②若、是第一象限角，且，

則；③函數(shù)一定是奇函數(shù)；④函數(shù)的

最小正周期為．上列四個命題中，正確的命題是 　　①④①、②②、③

設定義域為的奇函數(shù)是減函數(shù)，若當時，

，求的值．

試討論函數(shù)：的奇偶性。

(屆湖南師大附中高三月考)已知函數(shù)。

若函數(shù)的圖象關于點對稱，且，求的值；

設:,:，若是的充分條件，求實數(shù)的取值范圍。

問題1． 判斷下列函數(shù)的奇偶性：

；；

　；；

問題2．比較下列各組中兩個值的大小：

，，； ，．

問題3．求下列函數(shù)的單調(diào)遞增區(qū)間：①；

②；③；④

(全國Ⅰ)函數(shù)的一個單調(diào)增區(qū)間是

(福建)已知函數(shù)在區(qū)間上的最小值是，

則的最小值等于　　　　　　 　　　　　

為奇函數(shù)；函數(shù)為偶函數(shù)

為偶函數(shù)；函數(shù)為奇函數(shù)

函數(shù)的單調(diào)增區(qū)間可由

解出，單調(diào)減區(qū)間可由解出；　

函數(shù)的單調(diào)增區(qū)間可由

解出，單調(diào)減區(qū)間可由解出

三角函數(shù)的奇偶性和單調(diào)性具體如下表：

函數(shù)	奇偶性	單調(diào)區(qū)間
	奇	在上增 在減
	偶	在上增 在減
	奇	在上增

(四川)函數(shù)的最小正周期為　　 　　

(上海)函數(shù)的最小正周期 　　　　　　　

(福建)已知函數(shù)在區(qū)間上的最小值是，則

　的最小值等于　　 　　　

(安徽文)解不等式．

(天津)已知函數(shù)，．

(Ⅰ)求函數(shù)的最小正周期；

(Ⅱ)求函數(shù)在區(qū)間上的最小值和最大值．

(重慶)設．(Ⅰ)求的最大值及最小正周期；

(Ⅱ)若銳角滿足，求的值．

求函數(shù)的定義域.

函數(shù)的定義域為　　　　　

若方程有解，則　　　　 　

(江西)設函數(shù)，則為　　　

周期函數(shù)，最小正周期為　　　 周期函數(shù)，最小正周期為

周期函數(shù)，數(shù)小正周期為　　　 非周期函數(shù)

(全國Ⅱ)函數(shù)的最小正周期是　 　　2

函數(shù)的最小正周期為　　　　 　

函數(shù)的周期是　　　　　　

已知函數(shù)，求的定義域，判斷它的奇偶性，并求其值域

問題1． 求下列函數(shù)的定義域:

　； ；

問題2．求下列函數(shù)的值域：

；；；．

問題3．求下列函數(shù)的周期：

；；

問題4．已知函數(shù)的定義域為，值域為，求常數(shù)的值．

求三角函數(shù)的定義域實質就是解三角不等式(組)．一般可用三角函數(shù)的圖象或三角函數(shù)線確定三角不等式的解．列三角不等式，既要考慮分式的分母不能為零；偶次方根被開方數(shù)大于等于零；對數(shù)的真數(shù)大于零及底數(shù)大于零且不等于1，又要考慮三角函數(shù)本身的定義域；

求三角函數(shù)的值域的常用方法：①化為求代數(shù)函數(shù)的值域；②化為求的值域；③化為關于(或)的二次函數(shù)式；

三角函數(shù)的周期問題一般將函數(shù)式化為(其中為三角函數(shù)，)．

三角函數(shù)的定義域、值域及周期如下表：

函數(shù)	定義域	值域	周期

(天津)要得到函數(shù)的圖象，只需將函數(shù)的

圖象上所有的點的

橫坐標縮短到原來的倍(縱坐標不變),再向左平行移動個單位長度

橫坐標縮短到原來的倍(縱坐標不變)，再向右平行移動個單位長度

橫坐標伸長到原來的倍(縱坐標不變)，再向左平行移動個單位長度

橫坐標伸長到原來的倍(縱坐標不變)，再向右平行移動個單位長度

(江蘇)為了得到函數(shù)的圖像，只需把函數(shù)的圖像上所有的點

向左平移個單位長度，再把所得各點的橫坐標縮短到原來的倍(縱坐標不變)

向右平移個單位長度，再把所得各點的橫坐標縮短到原來的倍(縱坐標不變)

向左平移個單位長度，再把所得各點的橫坐標伸長到原來的倍(縱坐標不變)

向右平移個單位長度，再把所得各點的橫坐標伸長到原來的倍(縱坐標不變)

　(安徽)函數(shù)的圖象為，

①圖象關于直線對稱；②函數(shù)在區(qū)間內(nèi)是增函數(shù)；

③由的圖象向右平移個單位長度可以得到圖象．

以上三個論斷中，正確論斷的個數(shù)是　 　　　　　　　

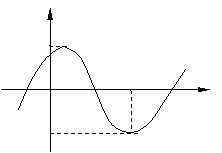(安徽)將函數(shù)的圖象按向量

平移，平移后的圖象如圖所示，

則平移后的圖象所對應函數(shù)的解析式是

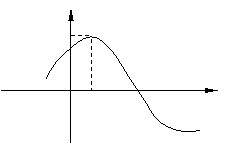
(福建)函數(shù),

)的部分圖象如圖，則　　

(福建)已知函數(shù)的最小正周期為，則該函數(shù)的圖象關于點對稱　　　 　　　　　　 關于直線對稱

關于點對稱　　　　　　　　　 關于直線對稱

(廣東文)已知簡諧運動的圖象經(jīng)過點，則該簡諧運動的最小正周期和初相分別為

，；，；，；，

(陜西)已知函數(shù)

(Ⅰ)求函數(shù)的最小正周期；(Ⅱ)求使函數(shù)取得最大值的集合.

(全國Ⅰ文)設函數(shù)圖像的一條對稱軸是直線.(Ⅰ)求；(Ⅱ)求函數(shù)的單調(diào)增區(qū)間；

(Ⅲ)畫出函數(shù)在區(qū)間上的圖像。

　(全國)已知函數(shù)是上的偶函數(shù)，其圖象關于點對稱，且在區(qū)間上是單調(diào)函數(shù)。求的值。