
 (
( 屆高三江西師大附中期中試題)若兩個向量
屆高三江西師大附中期中試題)若兩個向量 與
與 的夾角為
的夾角為 ,則稱向量“
,則稱向量“ ”為“向量積”,其長度
”為“向量積”,其長度 . 若
. 若 ,
, ,
, ,求
,求

 已知
已知 ,
, 與
與 的夾角為
的夾角為 ,則
,則 在
在 上的投影為
上的投影為
 向量
向量 都是非零向量,且
都是非零向量,且 ,求
,求 與
與 的夾角
的夾角
 已知兩單位向量
已知兩單位向量 與
與 的夾角為
的夾角為 ,若
,若 ,
, ,試求
,試求 與
與 的夾角。
的夾角。
 已知向量
已知向量 和
和 的夾角是
的夾角是 ,且
,且 ,
, ,則
,則
 設向量
設向量 滿足
滿足 ,
, ,則
,則
 已知向量
已知向量 的方向相同,且
的方向相同,且 ,
, ,則
,則
 在
在 中,
中, ,
, 的面積是
的面積是 ,若
,若 ,
, ,則
,則








 已知
已知 為原點,點
為原點,點 的坐標分別為
的坐標分別為 ,
, ,其中常數
,其中常數 ,點
,點 在線段
在線段 上,且有
上,且有
 ,則
,則 的最大值為
的最大值為 







 設
設 為平面上四個點,
為平面上四個點, ,
, ,
, ,且
,且 ,
, 

 ,則
,則 =
=
 設兩個向量
設兩個向量 、
、 ,滿足
,滿足 ,
, ,
, 、
、 的夾角為
的夾角為 ,若向量
,若向量 與向量
與向量 的夾角為鈍角,求實數
的夾角為鈍角,求實數 的取值范圍.
的取值范圍.
 (
( 屆高三湖北八校聯考)在
屆高三湖北八校聯考)在 中,
中,

 求
求 邊的長度;
邊的長度; 求
求  的值
的值
問題1. 有下列命題:①
有下列命題:① ;②
;②  ;③若
;③若 ,
,
則 ;④若
;④若 ,則
,則 當且僅當
當且僅當 時成立;⑤
時成立;⑤
⑥ 對任意
對任意 向量都成立;⑦對任意向量
向量都成立;⑦對任意向量 ,有
,有

其中正確命題的序號是
 (
( 福建)對于向量
福建)對于向量 和實數
和實數 ,下列命題中真命題是
,下列命題中真命題是
 若
若 ,則
,則 或
或
 若
若 ,則
,則 或
或
 若
若 ,則
,則 或
或
 若
若 ,則
,則
問題2. 已知
已知 中,
中, ,則
,則
 (
( 浙江)已知平面上三點
浙江)已知平面上三點 滿足
滿足 ,
,
則 的值等于
的值等于
 已知
已知 是兩個非零向量,且
是兩個非零向量,且 ,求
,求 與
與 的夾角
的夾角
 (
( 福建文)已知向量
福建文)已知向量 與
與 的夾角為
的夾角為 ,
, ,
, ,則
,則








問題3.( 蘇錫常鎮模擬)已知平面上三個向量
蘇錫常鎮模擬)已知平面上三個向量 ,它們之間的夾角均為
,它們之間的夾角均為 .
. 求證:
求證: ;
; 若
若
 ,求
,求 的取值范圍.
的取值范圍.
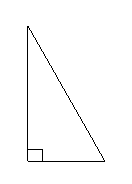
問題4. ( 湖北)如圖,在
湖北)如圖,在 中,已知
中,已知 ,若
,若
長為 的線段
的線段 以點
以點 為中點,問
為中點,問 與
與 的夾角
的夾角 取何值時
取何值時
 的值最大?并求出這個最大值.
的值最大?并求出這個最大值.
 注意向量夾角的概念和兩向量夾角的范圍;
注意向量夾角的概念和兩向量夾角的范圍;
 垂直的充要條件的應用;
垂直的充要條件的應用;
 當角為銳角或鈍角,求參數的范圍時注意轉化的等價性;
當角為銳角或鈍角,求參數的范圍時注意轉化的等價性;
 距離,角和垂直可以轉化到向量的數量積問題來解決.
距離,角和垂直可以轉化到向量的數量積問題來解決.
 平面向量數量積的概念;
平面向量數量積的概念;
 平面向量數量積的性質:
平面向量數量積的性質: ,
, ;
;
 向量垂直的充要條件:
向量垂直的充要條件: .
.
 (
( 全國Ⅰ)設平面向量
全國Ⅰ)設平面向量 、
、 、
、 的和
的和 如果向量
如果向量 、
、 、
、 ,
,
滿足 ,且
,且 順時針旋轉
順時針旋轉 后與
后與 同向,其中
同向,其中 ,則
,則

 ;
;
 ;
;
 ;
;

 (
( 山東)已知向量
山東)已知向量 ,且
,且 ,
, ,
,
則一定共線的三點是: 







 (
( 全國Ⅱ)在
全國Ⅱ)在 中,已知
中,已知 是
是 邊上一點,若
邊上一點,若 ,
,
 則
則








 (
( 北京)已知
北京)已知 是
是 所在平面內一點,
所在平面內一點, 為
為 邊中點,
邊中點,
且 ,那么
,那么 







 (
( 全國Ⅰ)
全國Ⅰ) 的外接圓的圓心為
的外接圓的圓心為 ,兩條邊上的高的交點為
,兩條邊上的高的交點為 ,
,  ,則實數
,則實數
 (
( 江西)已知等差數列
江西)已知等差數列 的前
的前 項和為
項和為 ,若
,若 ,且
,且 三點共線(該直線不過點
三點共線(該直線不過點 ),則
),則 等于
等于








 (
( 福建)已知
福建)已知 ,
, ,
, ,點
,點 在
在 內,且
內,且 ,設
,設
 ,則
,則










 (
( 上海文)在平行四邊形
上海文)在平行四邊形 中,下列結論中錯誤的是
中,下列結論中錯誤的是








 (
( 安徽文)在平行四邊形
安徽文)在平行四邊形 中,
中, ,
,
 為
為 的中點,則
的中點,則 (用
(用 表示)
表示)

 (
( 江西)如圖,在
江西)如圖,在 中,點
中,點 是
是 的中點,
的中點,
過點 的直線分別交直線
的直線分別交直線 ,
, 于不同的
于不同的
兩點 ,若
,若 ,
, ,
,
則 的值為
的值為
 考查下列四個命題:①對于實數
考查下列四個命題:①對于實數 和向量
和向量 ,恒有
,恒有 ;②對于實數
;②對于實數 和向量
和向量
 ,若
,若 ,則
,則 ;③
;③
 ,
,
則 ;④
;④ ,
, ,則
,則 ,⑤若
,⑤若 ,則存在唯一的
,則存在唯一的 ,使得
,使得 ;⑥以
;⑥以 為起點的三個向量
為起點的三個向量 的終點
的終點 在同一直線上的充要條件是
在同一直線上的充要條件是
 .則其中正確的命題的序號分別是
.則其中正確的命題的序號分別是
 已知
已知 中,
中, 是
是 內的一點,若
內的一點,若 則
則 是
是 的
的
 重心
重心  垂心
垂心  內心
內心  外心
外心
 若
若 是平面內的任意四點,給出下列式子:①
是平面內的任意四點,給出下列式子:① ;
;
② ;③
;③ .其中正確的有:
.其中正確的有:







 設
設 為非零向量,則下列命題中,真命題的個數是______
為非零向量,則下列命題中,真命題的個數是______
① 與
與 有相等的模;
有相等的模;
② 與
與 的方向相同;
的方向相同;
③ 與
與 的夾角為銳角;
的夾角為銳角;
④ 且
且 與
與 方向相反.
方向相反.
 若非零向量
若非零向量 滿足
滿足 ,則
,則 與
與 所成的角的大小為
所成的角的大小為
 向量
向量 ,則
,則 的最大值和最小值分別是
的最大值和最小值分別是
 設
設 是不共線的向量,
是不共線的向量, 與
與 共線,則實數
共線,則實數 的值是
的值是
 已知
已知 是兩個不共線的非零向量,它們的起點相同,且
是兩個不共線的非零向量,它們的起點相同,且 三個向量的終點在同一條直線上,求實數
三個向量的終點在同一條直線上,求實數 的值.
的值.
 已知四邊形
已知四邊形 的兩邊
的兩邊 的中點分別是
的中點分別是 ,求證:
,求證:
問題1.判斷下列命題是否正確,不正確的說明理由.
 若向量
若向量 與
與 同向,且
同向,且 ,則
,則 ;
;
 若向量
若向量 ,則
,則 與
與 的長度相等且方向相同或相反;
的長度相等且方向相同或相反;
 對于任意向量若
對于任意向量若 且
且 與
與 的方向相同,則
的方向相同,則 ;
;
 由于零向量
由于零向量 方向不確定,故
方向不確定,故 不能與任意向量平行;
不能與任意向量平行;
 向量
向量 ,則向量
,則向量 與
與 方向相同或相反;
方向相同或相反;
 向量
向量 與
與 是共線向量,則
是共線向量,則 四點共線;
四點共線;
 起點不同,但方向相同且模相等的幾個向量是相等向量.
起點不同,但方向相同且模相等的幾個向量是相等向量.
 若
若 ,且
,且 ,則
,則
問題2. (
( 洛陽模擬)設
洛陽模擬)設 是兩個不共線的向量,若
是兩個不共線的向量,若 與
與
 共線,則實數
共線,則實數
 若點
若點 為
為 的外心,且
的外心,且 ,
,
則 的內角
的內角
 (
( 新課程)
新課程) 是平面上的一定點,
是平面上的一定點, 是平面上不共線的三個點,動點
是平面上不共線的三個點,動點
滿足 ,則
,則 的軌跡一定通過
的軌跡一定通過 的
的  外心
外心
 內心
內心  重心
重心  垂心
垂心
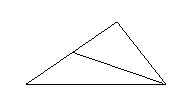
 (
( 廣東)
廣東) 是
是 的邊
的邊 上的中點,則向量
上的中點,則向量








問題3. (
( 湖南)如圖,
湖南)如圖,  , 點
, 點 在由射線
在由射線 , 線段
, 線段 及
及 的延長線圍成的區域內(不含邊界)運動,且
的延長線圍成的區域內(不含邊界)運動,且 ,則
,則 的取值范圍是
的取值范圍是
 ;當
;當 時,
時,  的取值范圍是
的取值范圍是
 (
( 陜西)如圖,平面內有三個向量
陜西)如圖,平面內有三個向量 ,其中
,其中 與
與 的夾角為
的夾角為 ,
, 與
與 的夾角為
的夾角為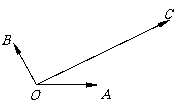
 ,且
,且 ,
, .若
.若
 ,
,
則 的值為
的值為
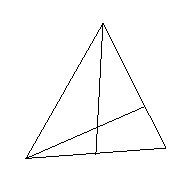 問題4. (
問題4. ( 屆高三石家莊模擬)如圖,在
屆高三石家莊模擬)如圖,在 中,
中,
點 是
是 的中點,點
的中點,點 在邊
在邊 上,且
上,且 ,
,
 與
與 相交于點
相交于點 ,求
,求 的值
的值
 充分理解向量的概念和向量的表示;
充分理解向量的概念和向量的表示;  數形結合的方法的應用;
數形結合的方法的應用;
 用基底向量表示任一向量唯一性;
用基底向量表示任一向量唯一性;  向量的特例
向量的特例 和單位向量,要考慮周全.
和單位向量,要考慮周全.
 用好“封閉折線的向量和等于零向量”;
用好“封閉折線的向量和等于零向量”; 由共線求交點的方法:待定系數
由共線求交點的方法:待定系數 .
.
 向量的概念及向量的表示;
向量的概念及向量的表示;  向量的加法、減法與實數乘向量概念與運算律;
向量的加法、減法與實數乘向量概念與運算律;
 兩向量共線定理與平面向量基本定理.
兩向量共線定理與平面向量基本定理.
 (
( 江蘇)
江蘇) 中,
中, ,
, ,則
,則 的周長為
的周長為








 (
( 全國)
全國) 中,
中, 分別是三個內角
分別是三個內角 的對邊,.如果
的對邊,.如果 成等差數列,
成等差數列, ,
, 的面積為
的面積為 ,那么
,那么








 (
( 北京春)在
北京春)在 中,
中, 、
、 、
、 分別是的對邊長,已知
分別是的對邊長,已知 、
、 、
、
成等比數列,且,求的大小及的值
 (
( 湖南)已知在
湖南)已知在 中,
中, ,
, ,
,
求角 的大小.
的大小.
 (
( 上海) 在
上海) 在 中,
中, 分別是三個內角
分別是三個內角 的對邊.若
的對邊.若 ,
, ,求
,求 的面積
的面積 .
.

 (
( 天津)如圖,在
天津)如圖,在 中,
中, ,
,
 ,
, .
. 求
求 的值;
的值; 求
求 的值.
的值.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com