
 (
( 北京)平面
北京)平面 的斜線
的斜線 交
交 于點
于點 ,過定點
,過定點 的動直線
的動直線 與
與 垂直,且交
垂直,且交
于點 ,則動點
,則動點 的軌跡是
的軌跡是  一條直線
一條直線  一個圓
一個圓  一個橢圓
一個橢圓  雙曲線的一支
雙曲線的一支
 (
( 北京文)設
北京文)設 、
、 、
、 、
、 是空間四個不同的點,在下列命題中,不正確的是
是空間四個不同的點,在下列命題中,不正確的是
 若
若 與
與 共面,則
共面,則 與
與 共面
共面
 若
若 與
與 是異面直線,則
是異面直線,則 與
與 是異面直線
是異面直線
 若
若 ,
, ,則
,則

 若
若 ,
, ,則
,則
 (
( 重慶)對于任意的直線
重慶)對于任意的直線 與平面
與平面 ,在平面
,在平面 內必有直線
內必有直線 ,使
,使 與
與
 平行
平行
 相交
相交
 垂直
垂直
 互為異面直線
互為異面直線
 (
( 全國Ⅰ)在正方形
全國Ⅰ)在正方形 中,過對角線
中,過對角線 的一個平面交
的一個平面交 于
于 ,交
,交 于
于 ,則
,則
①
四邊形 一定是平行四邊形;
一定是平行四邊形;
②
四邊形 有可能是正方形
有可能是正方形
③
四邊形 在底面
在底面 內的投影一定是正方形
內的投影一定是正方形
④
四邊形 有可能垂直于平面
有可能垂直于平面
以上結論正確的為 (寫出所有正確結論的編號)
 (
( 浙江)若
浙江)若 是兩條異面直線
是兩條異面直線 外的任意一點,則
外的任意一點,則
 過點
過點 有且僅有一條直線與
有且僅有一條直線與 都平行
都平行 過點
過點 有且僅有一條直線與
有且僅有一條直線與 都垂直
都垂直
 過點
過點 有且僅有一條直線與
有且僅有一條直線與 都相交
都相交  過點
過點 有且僅有一條直線與
有且僅有一條直線與 都異面
都異面
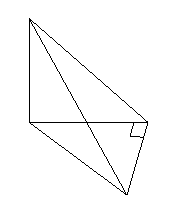
 (
( 天津)如圖,
天津)如圖, 平面
平面 ,
, ,
,
且 ,則異面直線
,則異面直線 與
與 所成角
所成角
的余弦值為
 (
( 江西文)如圖,已知三棱錐
江西文)如圖,已知三棱錐 的側棱
的側棱
 、
、 、
、 兩兩垂直,且
兩兩垂直,且 ,
, ,
,
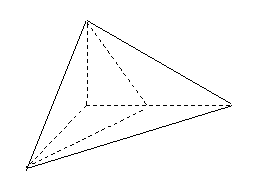
 是
是 的中點.
的中點. 略;
略; 求異面直線
求異面直線 與
與 所成的角;
所成的角;
 略.
略.
問題1. (
( 上海)若空間中有四個點,則“這四個點中有三點在同一直線上”
上海)若空間中有四個點,則“這四個點中有三點在同一直線上”
是“這四個點在同一平面上”的
 充分非必要條件;
充分非必要條件; 必要非充分條件;
必要非充分條件; 充要條件;
充要條件; 非充分非必要條件.
非充分非必要條件.
 (
( 全國Ⅲ)不共面的四個定點到平面
全國Ⅲ)不共面的四個定點到平面 的距離都相等,這樣的平面
的距離都相等,這樣的平面 共有
共有

 個
個

 個
個

 個
個

 個
個
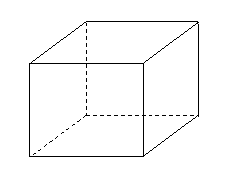
 (
( 全國Ⅱ)正方體
全國Ⅱ)正方體 中,
中,
 、
、 、
、 分別是
分別是 、
、 、
、 的中點.
的中點.
那么,正方體的過 、
、 、
、 的截面圖形是
的截面圖形是
 三角形
三角形 四邊形
四邊形 五邊形
五邊形 六邊形
六邊形

 如圖,
如圖, ,
, 、
、 ,
, ,
,
且 ,直線
,直線 ,過
,過 、
、 、
、 三點
三點
的平面記作 ,則
,則 與
與 的交線必通過
的交線必通過
 點
點 ;
;
 點
點 ;
;
 點
點 但不通過點
但不通過點 ;
;  點
點 和點
和點
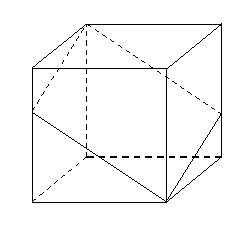
 (
( 江蘇)如圖,已知
江蘇)如圖,已知 是棱長
是棱長
為 的正方體,點
的正方體,點 在
在 上,點
上,點 在
在 上,
上,
且 .
. 求證:
求證: 四點共面;(
四點共面;( 分)
分)
 略;
略; 略.
略.
問題2.( 全國Ⅱ)如圖,在直三棱柱
全國Ⅱ)如圖,在直三棱柱 中,
中, ,
, 、
、 分別
分別
為 、
、 的中點.
的中點. 證明:
證明: 為異面直線
為異面直線 與
與 的公垂線;
的公垂線; 略.
略.
( 要求用傳統方法和向量法,注意書寫的規范性)
 證明:方法
證明:方法 (用傳統方法):
(用傳統方法):
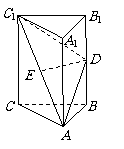
方法 (用向量法):
(用向量法):

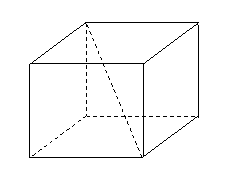
問題3.如圖,在正方體 中,
中,
棱長 ,
, 求證:
求證: 與
與 是異面直線;
是異面直線;
 求
求 于
于 間的距離.
間的距離.
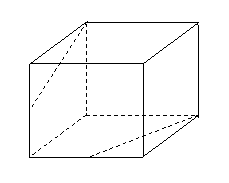
問題4.( 上海春)在棱長為
上海春)在棱長為 的正方體
的正方體 中,
中, 、
、 分別是
分別是 、
、 的中點,求異面直線
的中點,求異面直線 與
與 所成的角( 要求用傳統方法和向量法,注意書寫的規范性).
所成的角( 要求用傳統方法和向量法,注意書寫的規范性).
解法1(傳統方法):
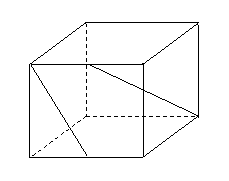
解法2(向量法):
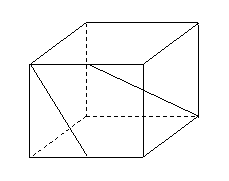
 (三)課后作業:
(三)課后作業:
 如圖,在正方體
如圖,在正方體 中,
中, 、
、 分別
分別
是 、
、 的中點,求證:
的中點,求證:
① 、
、 、
、 、
、 四點共面;
四點共面;
② 、
、 、
、 三點共線.
三點共線.
 角
角 與
與 的兩邊分別平行,當
的兩邊分別平行,當
 時,
時, 
 已知
已知 的直觀圖是邊長為
的直觀圖是邊長為 的等邊
的等邊 ,那么
,那么 的面積為
的面積為









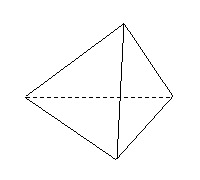
 如圖,在空間四邊形
如圖,在空間四邊形 中,已知
中,已知 ,
,
 ,且
,且 ,對角線
,對角線 ,
,
 ,求
,求 與
與 所成的角.
所成的角.
 公理
公理 :如果一條直線上的兩點在一個平面內,那么這條直線上所有的點都在這個平面內.
:如果一條直線上的兩點在一個平面內,那么這條直線上所有的點都在這個平面內.
作用:①作為判斷和證明是否在平面內的依據;②證明點在某平面內的依據;③檢驗某面是否平面的依據.
公理 :如果兩個平面有一個公共點,那么它們還有其他公共點,且所有這些公共點的集合是一條過這個公共點的直線.
:如果兩個平面有一個公共點,那么它們還有其他公共點,且所有這些公共點的集合是一條過這個公共點的直線.
作用:①作為判斷和證明兩平面是否相交;②證明點在某直線上;③證明三點共線;
④證明三線共點.
公理 : 經過不在同一條直線上的三點,有且只有一個平面.
: 經過不在同一條直線上的三點,有且只有一個平面.
推論 :經過一條直線和直線外的一點有且只有一個平面.
:經過一條直線和直線外的一點有且只有一個平面.
推論 :經過兩條相交直線有且只有一個平面.
:經過兩條相交直線有且只有一個平面.
推論 :經過兩條平行直線有且只有一個平面.
:經過兩條平行直線有且只有一個平面.
作用:公理 及其推論是空間里確定平面的依據,也是證明兩個平面重合的依據,還為立體幾何問題轉化為平面幾何問題提供了理論依據和具體辦法.
及其推論是空間里確定平面的依據,也是證明兩個平面重合的依據,還為立體幾何問題轉化為平面幾何問題提供了理論依據和具體辦法.
 證明三點均在兩個平面的交線上,可以推證三點共線
證明三點均在兩個平面的交線上,可以推證三點共線
 證明直線共面通常的方法:
證明直線共面通常的方法: 先由其中兩條直線確定一個平面,再證明其余的直線都在此平面內(納入法);
先由其中兩條直線確定一個平面,再證明其余的直線都在此平面內(納入法); 分別過某些點作多個平面,然后證明這些平面重合(重合法);
分別過某些點作多個平面,然后證明這些平面重合(重合法);
也可利用共面向量定理來證明.
 公理
公理 是證明直線共點的依據,應該這樣理解:
是證明直線共點的依據,應該這樣理解: 如果
如果 、
、 是交點,那么
是交點,那么 是交線;
是交線;
 如果兩個不同平面有三個或者更多的交點,那么它們共面;
如果兩個不同平面有三個或者更多的交點,那么它們共面;
 如果
如果 ,點
,點 是a、b的一個公共點,那么
是a、b的一個公共點,那么
 求兩條異面直線所成的角,首先要判斷兩條異面直線是否垂直,若垂直,則它們所成的角為
求兩條異面直線所成的角,首先要判斷兩條異面直線是否垂直,若垂直,則它們所成的角為 ;若不垂直,則利用平移法求角,一般的步驟是“作(找)-證-算”.注意,異面直線所成角的范圍是
;若不垂直,則利用平移法求角,一般的步驟是“作(找)-證-算”.注意,異面直線所成角的范圍是 ;求異面直線所成角的方法:①平移法:一般情況下應用平行四邊形的對邊、梯形的平行對邊、三角形的中位線進行平移.
;求異面直線所成角的方法:①平移法:一般情況下應用平行四邊形的對邊、梯形的平行對邊、三角形的中位線進行平移.
②向量法:設 、
、 分別為異面直線
分別為異面直線 、
、 的方向向量,
的方向向量,
則兩異面直線所成的角
 ;③補體法
;③補體法
 兩條異面直線的公垂線:①定義:和兩條異面直線都垂直相交的直線,叫做異面直線的公垂線;②證明:異面直線公垂線的證明常轉化為證明公垂線與兩條異面直線分別垂直.
兩條異面直線的公垂線:①定義:和兩條異面直線都垂直相交的直線,叫做異面直線的公垂線;②證明:異面直線公垂線的證明常轉化為證明公垂線與兩條異面直線分別垂直.
 兩條異面直線的距離:①定義:兩條異面直線的公垂線在這兩條異面直線間的線段的長度.
兩條異面直線的距離:①定義:兩條異面直線的公垂線在這兩條異面直線間的線段的長度.
②計算方法: 公垂線法;
公垂線法; 轉化成線面距離(點面距離);
轉化成線面距離(點面距離); 轉化成面面距離.
轉化成面面距離.
 (
( 遼寧)已知雙曲線的中心在原點,離心率為
遼寧)已知雙曲線的中心在原點,離心率為 .若它的一條準線與拋物線
.若它的一條準線與拋物線 的準線重合,則該雙曲線與拋物線
的準線重合,則該雙曲線與拋物線 的交點到原點的距離是
的交點到原點的距離是








 (
( 湖北)雙曲線
湖北)雙曲線 的左準線為
的左準線為 ,左焦點和右焦點分別為
,左焦點和右焦點分別為 和
和 ;拋物線
;拋物線 的準線為
的準線為 ,焦點為
,焦點為 與
與 的一個交點為
的一個交點為 ,則
,則 等于
等于 







 (
( 天津文)設雙曲線
天津文)設雙曲線
 的離心率為
的離心率為 ,且它的一條準線與拋物線
,且它的一條準線與拋物線 的準線重合,則此雙曲線的方程為
的準線重合,則此雙曲線的方程為








 (
( 四川)設
四川)設 、
、 分別是橢圓
分別是橢圓 的左、右焦點.
的左、右焦點.
 若
若 是該橢圓上的一個動點,求
是該橢圓上的一個動點,求 的最大值和最小值;
的最大值和最小值;
 設過定點
設過定點 的直線
的直線 與橢圓交于不同的兩點
與橢圓交于不同的兩點 、
、 ,且
,且 為銳角(其中
為銳角(其中 為坐標原點),求直線
為坐標原點),求直線 的斜率
的斜率 的取值范圍.
的取值范圍.
 (
( 上海)點
上海)點 、
、 分別是橢圓
分別是橢圓 長軸的左、右端點,點
長軸的左、右端點,點 是橢圓的右焦點,點
是橢圓的右焦點,點 在橢圓上,且位于
在橢圓上,且位于 軸上方,
軸上方, .
. 求點
求點 的坐標;
的坐標; 設
設 是橢圓長軸
是橢圓長軸 上的一點,
上的一點, 到直線
到直線 的距離等于
的距離等于 ,求橢圓上的點到點
,求橢圓上的點到點 的距離
的距離 的最小值.
的最小值.
 設集合
設集合 ,
, ,且
,且 ,求實數
,求實數 的取值范圍.
的取值范圍.
 正方體
正方體 的面
的面 中有一動點
中有一動點 到直線
到直線 和
和 的距離相等,則動點
的距離相等,則動點 的軌跡是
的軌跡是  一線段
一線段  拋物線的一部分
拋物線的一部分  橢圓
橢圓  橢圓的一部分
橢圓的一部分
 要建造一座跨度為
要建造一座跨度為 米,拱高為
米,拱高為 米的拋物線拱橋,建橋時,每隔
米的拋物線拱橋,建橋時,每隔 米用一根柱支撐,兩邊的柱長應為
米用一根柱支撐,兩邊的柱長應為
 (
( 南京模擬)已知拋物線
南京模擬)已知拋物線
 的焦點
的焦點 恰好是橢圓
恰好是橢圓 的
的
右焦點,且兩條曲線的公共點的連線過 ,則該橢圓的離心率為
,則該橢圓的離心率為








 若橢圓
若橢圓 和雙曲線
和雙曲線 有共同的焦點
有共同的焦點 、
、 且
且 是兩條曲線的一個交點,則
是兩條曲線的一個交點,則 的面積是
的面積是 







 已知橢圓的中心在原點,離心率
已知橢圓的中心在原點,離心率 ,且它的一個焦點與拋物線
,且它的一個焦點與拋物線 的焦點重合,則此橢圓方程為
的焦點重合,則此橢圓方程為 







 (
( 屆高三攸縣一中)已知橢圓
屆高三攸縣一中)已知橢圓 與雙曲線
與雙曲線 有相同的準線,
有相同的準線,
則動點 的軌跡為
的軌跡為  橢圓的一部分
橢圓的一部分
 雙曲線的一部分
雙曲線的一部分
 拋物線的一部分
拋物線的一部分  直線的一部分
直線的一部分
 已知圓
已知圓 過雙曲線
過雙曲線 的一個頂點和一個焦點,且圓心在此雙曲線上,則圓心到雙曲線中心的距離是
的一個頂點和一個焦點,且圓心在此雙曲線上,則圓心到雙曲線中心的距離是
 求與圓
求與圓 :
: 和圓
和圓 :
: 都外切的圓的圓心
都外切的圓的圓心 的軌跡方程為
的軌跡方程為
 對于任意
對于任意 ,拋物線
,拋物線 與
與 軸交于
軸交于 兩點,以
兩點,以 表示該兩點的距離,則
表示該兩點的距離,則 的值是
的值是








問題1.( 四川)已知兩定點
四川)已知兩定點
 滿足條件
滿足條件 的點
的點 的軌跡是曲線
的軌跡是曲線 ,直線
,直線 與曲線
與曲線 交于
交于 、
、 兩點。如果
兩點。如果 且曲線
且曲線 上存在點
上存在點 ,使
,使 求
求 的值和
的值和 的面積
的面積 .
.
問題2.( 湖南)已知橢圓
湖南)已知橢圓 :
: ,拋物線
,拋物線 :
: ,
,
且 、
、 的公共弦
的公共弦 過橢圓
過橢圓 的右焦點
的右焦點
 當
當 軸時,求
軸時,求 、
、 的值,并判斷拋物線
的值,并判斷拋物線 的焦點是否在直線
的焦點是否在直線 上;
上;
 是否存在
是否存在 、
、 的值,使拋物線
的值,使拋物線 的焦點恰在直線
的焦點恰在直線 上?若存在,
上?若存在,
求出符合條件的 、
、 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
問題3.( 寧夏)在平面直角坐標系
寧夏)在平面直角坐標系 中,經過點
中,經過點 且斜率為
且斜率為 的直線
的直線 與橢圓
與橢圓 有兩個不同的交點
有兩個不同的交點 和
和 .
. 求
求 的取值范圍;
的取值范圍;
 設橢圓與
設橢圓與 軸正半軸、
軸正半軸、 軸正半軸的交點分別為
軸正半軸的交點分別為 ,是否存在常數
,是否存在常數 ,使得向量
,使得向量 與
與 共線?如果存在,求
共線?如果存在,求 值;如果不存在,請說明理由.
值;如果不存在,請說明理由.
問題4.( 重慶) 已知一列橢圓
重慶) 已知一列橢圓 :
: ,
, .
. ….
….
 若橢圓
若橢圓 上有一點
上有一點 ,使
,使 到右準線
到右準線 的距離
的距離 是
是 與
與
的等差中項,其中 、
、 分別是
分別是 的左、右焦點。
的左、右焦點。
 試證:
試證: ≤
≤ (
( ≥
≥ );
);
 取
取 ,并用
,并用 表示
表示 的面積,
的面積,
試證: 且
且 (
( ≥
≥ )
)
問題5.某工程要挖一個橫斷面為半圓柱形的坑,挖出的土只能沿道路 、
、 運到
運到 處(如圖),已知
處(如圖),已知 ,
, ,
, ,試說明怎樣運土最省工
,試說明怎樣運土最省工

 圓錐曲線綜合問題包含內部綜合、圓錐曲線與其它章節的綜合以及運用圓錐曲線解決實際問題前者用到圓錐曲線重要的思想與方法,是高考的熱點;圓錐曲線與其它章節的綜合要注意各部分知識點的聯系,后者要通過建立數學模型,把實際問題轉化為數學問題求解.
圓錐曲線綜合問題包含內部綜合、圓錐曲線與其它章節的綜合以及運用圓錐曲線解決實際問題前者用到圓錐曲線重要的思想與方法,是高考的熱點;圓錐曲線與其它章節的綜合要注意各部分知識點的聯系,后者要通過建立數學模型,把實際問題轉化為數學問題求解.
 對于較為綜合的解析幾何問題,必須對題目的內涵進行深刻挖掘的基礎上,應用整體思想,構建轉化的“框架”,然后,綜合利用代數手段解題.
對于較為綜合的解析幾何問題,必須對題目的內涵進行深刻挖掘的基礎上,應用整體思想,構建轉化的“框架”,然后,綜合利用代數手段解題.
 圓錐曲線的定義是解決綜合題的基礎,定義在本質上揭示了平面上的動點與定點(或定直線)的距離滿足某種特殊關系,從數形結合思想去理解圓錐曲線中的參數(
圓錐曲線的定義是解決綜合題的基礎,定義在本質上揭示了平面上的動點與定點(或定直線)的距離滿足某種特殊關系,從數形結合思想去理解圓錐曲線中的參數( 等)的幾何意義以及這些參數間的相互關系,進而通過它們之間組成題設條件的轉化.
等)的幾何意義以及這些參數間的相互關系,進而通過它們之間組成題設條件的轉化.
 綜合題中常常離不開直線與圓錐曲線的位置,因此,要樹立將直線與圓錐曲線方程聯立,應用判別式、韋達定理的意識.
綜合題中常常離不開直線與圓錐曲線的位置,因此,要樹立將直線與圓錐曲線方程聯立,應用判別式、韋達定理的意識.
 解析幾何應用問題的解題關鍵是建立適當的坐標系,合理建立曲線模型,然后轉化為相應的代數問題作出定量或定性的分析與判斷.
解析幾何應用問題的解題關鍵是建立適當的坐標系,合理建立曲線模型,然后轉化為相應的代數問題作出定量或定性的分析與判斷.
 (
( 重慶)已知橢圓
重慶)已知橢圓 的方程為
的方程為 ,雙曲線
,雙曲線 的左、右焦點分別為
的左、右焦點分別為 的左、右頂點,而
的左、右頂點,而 的左、右頂點分別是
的左、右頂點分別是 的左、右焦點.(Ⅰ)求雙曲線
的左、右焦點.(Ⅰ)求雙曲線 的方程;
的方程;
(Ⅱ)若直線 :
: 與橢圓
與橢圓 及雙曲線
及雙曲線 都恒有兩個不同的交點,且
都恒有兩個不同的交點,且 與
與 的兩個交點
的兩個交點 和
和 滿足
滿足 (其中
(其中 為原點),求
為原點),求 的取值范圍.
的取值范圍.
 (
( 江西)
江西) 是雙曲線
是雙曲線 的右支上一點,
的右支上一點, 分別是圓
分別是圓
和 上的點,則
上的點,則 的最大值為
的最大值為 







 (
( 重慶)如圖,中心在原點
重慶)如圖,中心在原點 的橢圓的右焦點為
的橢圓的右焦點為 ,右準線
,右準線 的方程為:
的方程為: .
.
 求橢圓的方程;
求橢圓的方程; 在橢圓上任取三個不同點
在橢圓上任取三個不同點 ,使
,使
證明: 為定值,并求此定值.
為定值,并求此定值.
 (
( 全國Ⅰ)已知橢圓的中心為坐標原點
全國Ⅰ)已知橢圓的中心為坐標原點 ,焦點在
,焦點在 軸上,斜率為
軸上,斜率為 且過橢圓右焦點
且過橢圓右焦點 的直線交橢圓于
的直線交橢圓于 、
、 兩點,
兩點, 與
與 共線。
共線。
(Ⅰ)求橢圓的離心率;
(Ⅱ)設 為橢圓上任意一點,且
為橢圓上任意一點,且
 ,證明
,證明 為定值.
為定值.
 (
( 全國Ⅱ)
全國Ⅱ) 、
、 、
、 、
、 四點都在橢圓
四點都在橢圓 上,
上, 為橢圓在
為橢圓在 軸正半軸上的焦點.已知
軸正半軸上的焦點.已知 與
與 共線,
共線, 與
與 共線,且
共線,且 .求四邊形
.求四邊形 的面積的最小值和最大值.
的面積的最小值和最大值.
 (
( 浙江)已知雙曲線的中心在原點,右頂點為
浙江)已知雙曲線的中心在原點,右頂點為 ,點
,點 、
、 在雙曲線的右支上,點
在雙曲線的右支上,點 到直線
到直線 的距離為
的距離為 ,
,
 若直線
若直線 的斜率為
的斜率為 ,且
,且 , 求實數
, 求實數 的取值范圍;
的取值范圍;
 當
當 時,
時, 的內心恰好是點
的內心恰好是點 ,求此雙曲線的方程.
,求此雙曲線的方程.

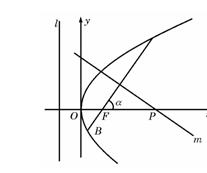 (
( 重慶文)如圖,傾斜角為
重慶文)如圖,傾斜角為 的直線經過拋物線
的直線經過拋物線 的焦點
的焦點 ,且與拋物線交于
,且與拋物線交于 、
、 兩點.
兩點.
 求拋物線的焦點
求拋物線的焦點 的坐標及準線
的坐標及準線 的方程;
的方程;
 若
若 為銳角,作線段
為銳角,作線段 的垂直平分線
的垂直平分線 交
交 軸于點
軸于點 ,證明:
,證明: 為定值,并求此定值.
為定值,并求此定值.
 (
( 山東)已知橢圓
山東)已知橢圓 的中心在坐標原點,焦點在
的中心在坐標原點,焦點在 軸上,橢圓
軸上,橢圓 上的點到焦點距離的最大值為
上的點到焦點距離的最大值為 ,最小值為
,最小值為 .
.
(Ⅰ)求橢圓 的標準方程;
的標準方程;
(Ⅱ)若直線 :
: 與橢圓
與橢圓 相交于
相交于 ,
, 兩點(
兩點( 不是左右頂點),且以
不是左右頂點),且以 為直徑的圓過橢圓
為直徑的圓過橢圓 的右頂點,求證:直線
的右頂點,求證:直線 過定點,并求出該定點的坐標.
過定點,并求出該定點的坐標.
 已知橢圓
已知橢圓 (
( )的右焦點為
)的右焦點為 ,過
,過 作直線與橢圓相交于
作直線與橢圓相交于 、
、 兩點,若有
兩點,若有 ,求橢圓離心率的取值范圍.
,求橢圓離心率的取值范圍.
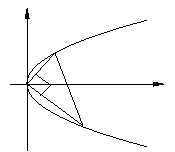
 過拋物線
過拋物線 的頂點任意作兩條互相垂直的弦
的頂點任意作兩條互相垂直的弦 、
、 ,
,
求證: 交拋物線的對稱軸上一定點.
交拋物線的對稱軸上一定點.

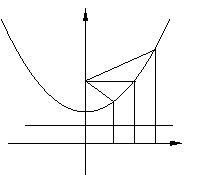 如圖,在雙曲線
如圖,在雙曲線 的上支上有三點
的上支上有三點 ,
,
 ,
, ,它們與點
,它們與點 的距離成等差數列.
的距離成等差數列.
 求
求 的值;
的值; 證明:線段
證明:線段 的垂直平分線經過
的垂直平分線經過
某一定點,并求此點坐標.
 在幾何問題中,有些幾何量與參數無關,這就構成了定值問題,解決這類問題一種思路是進行一般計算推理求出其結果;另一種是通過考查極端位置,探索出“定值”是多少,然后再進行一般性證明或計算,即將該問題涉及的幾何式轉化為代數式或三角形式,證明該式是恒定的.如果試題以客觀題形式出現,特殊方法往往比較奏效.
在幾何問題中,有些幾何量與參數無關,這就構成了定值問題,解決這類問題一種思路是進行一般計算推理求出其結果;另一種是通過考查極端位置,探索出“定值”是多少,然后再進行一般性證明或計算,即將該問題涉及的幾何式轉化為代數式或三角形式,證明該式是恒定的.如果試題以客觀題形式出現,特殊方法往往比較奏效.
 對滿足一定條件曲線上兩點連結所得直線過定點或滿足一定條件的曲線過定點問題,設該直線(曲線)上兩點的坐標,利用坐標在直線(或曲線)上,建立點的坐標滿足的方程(組),求出相應的直線(或曲線),然后再利用直線(或曲線)過定點的知識加以解決.
對滿足一定條件曲線上兩點連結所得直線過定點或滿足一定條件的曲線過定點問題,設該直線(曲線)上兩點的坐標,利用坐標在直線(或曲線)上,建立點的坐標滿足的方程(組),求出相應的直線(或曲線),然后再利用直線(或曲線)過定點的知識加以解決.
 解析幾何的最值和范圍問題,一般先根據條件列出所求目標的函數關系式,然后根據函數關系式的特征選用參數法、配方法、判別式法、不等式法、單調性法、導數法以及三角函數最值法等求出它的最大值和最小值.
解析幾何的最值和范圍問題,一般先根據條件列出所求目標的函數關系式,然后根據函數關系式的特征選用參數法、配方法、判別式法、不等式法、單調性法、導數法以及三角函數最值法等求出它的最大值和最小值.
 (二)典例分析:
(二)典例分析:
問題1. ( 廣東)在平面直角坐標系
廣東)在平面直角坐標系 中,
中,
拋物線 上異于坐標原點
上異于坐標原點 的兩不同動點
的兩不同動點 、
、 滿足
滿足 .
.
(Ⅰ)求 得重心
得重心 的軌跡方程;
的軌跡方程;
(Ⅱ) 的面積是否存在最小值?若存在,請求出最小值;
的面積是否存在最小值?若存在,請求出最小值;
若不存在,請說明理由.
問題2.已知橢圓 上的兩個動點
上的兩個動點 及定點
及定點 ,
, 為橢圓的左焦點,且
為橢圓的左焦點,且 ,
, ,
, 成等差數列.
成等差數列. 求證:線段
求證:線段 的垂直平分線經過一個定點
的垂直平分線經過一個定點 ;
;
 設點
設點 關于原點
關于原點 的對稱點是
的對稱點是 ,求
,求 的最小值及相應的
的最小值及相應的 點坐標.
點坐標.
問題3.( 全國Ⅱ)已知拋物線
全國Ⅱ)已知拋物線 的焦點為
的焦點為 ,
, 、
、 是拋物線上的兩動點,且
是拋物線上的兩動點,且 (
( ).過
).過 、
、 兩點分別作拋物線的切線,設其交點為
兩點分別作拋物線的切線,設其交點為 .
.
(Ⅰ)證明 為定值;
為定值;
(Ⅱ)設 的面積為
的面積為 ,寫出
,寫出 的表達式,并求
的表達式,并求 的最小值.
的最小值.
問題4.直線 :
: 和雙曲線
和雙曲線 的左支交于
的左支交于 、
、 兩點,直線
兩點,直線 過點
過點 和線段
和線段 的中點
的中點 ,求
,求 在
在 軸上的截距
軸上的截距 的取值范圍.
的取值范圍.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com