日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

(浙江)設集合＝|，，是三角形的三邊長，

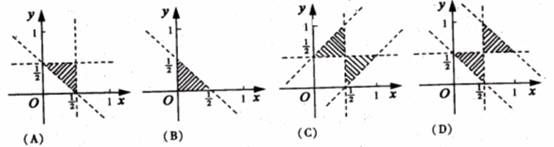
則所表示的平面區域(不含邊界的陰影部分)是

(天津文)設變量滿足約束條件則目標函數的最大值為　　　 　　　　 　　　 　　　　　　 　　　　　　　

(湖北)已知平面區域由以、、為頂點的三角形內部和邊界組成.若在區域上有無窮多個點可使目標函數取得最小值，則

(浙江)設為實數，若，則的取值范圍是　　　　　 　　　

(安徽文)如果點在平面區域上,點在曲線_，上，那么 最小值為 

(湖南)設集合，，，的取值范圍是　　　　 ；若，且的最大值為，則的值是　　　　　　　　

(江蘇)設變量滿足約束條件，則的最大值為　　 　　　

(四川)某廠生產甲產品每千克需用原料和原料分別為千克，生產乙產品每千克需用原料和原料分別為千克。甲、乙產品每千克可獲利潤分別為元。月初一次性購進本月用原料、各千克。要計劃本月生產甲、乙兩種產品各多少千克才能使月利潤總額達到最大。在這個問題中，設全月生產甲、乙兩種產品分別為千克、千克，月利潤總額為元，那么，用于求使總利潤最大的數學模型中，約束條件為

(屆高三重慶酉陽一中四檢)已知滿足約束條件,

則的最大值為　　　　　　 　　

　原點和點在直線的兩側，則的取值范圍是　　　　　　 　　

如果實數、滿足, 目標函數的最大值為, 最小值，那么實數的值為　　 　　　　　　　　　　不存在

(屆高三西安八校第一次月考)已知，則的最小值為　　　　　 　　

(蘇州中學模擬)如圖，目標函數的可行域為四邊形

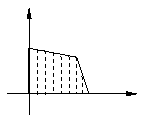(含邊界)，若()是該目標函數的最優解，則的取值范圍是

已知，則是的

充分不必要條件必要不充分條件既不充分也不必要條件充要條件

問題1．不等式表示的平面區域在直線的　　

　　 左上方　　　 　 右上方　　　　 左下方 　　　　 右下方

(全國Ⅰ)在坐標平面上，不等式組所表示的平面區域的面積為

畫出不等式組表示的平面區域，并回答下列問題：

①指出的取值范圍；②平面區域內有多少個整點？(盡可能多種解法)

已知點、在直線的異側，則的取值范圍是　　

問題2．(湖南)已知點在不等式組表示的平面區域上運動，則的取值范圍是　　 　

(遼寧)已知變量滿足約束條件則的取值范圍是

(湖南)已知則的最小值是　　　　　

(重慶)已知變量滿足約束條件：≤≤,≤≤.若目標

函數 (其中)僅在點處取得最大值，求的取值范圍.

問題3．制訂投資計劃時，不僅要考慮可能獲得的利益，而且要考慮可能出現的虧損。

某投資人打算投資甲、乙兩個項目.根據預測，甲、乙兩個項目可能的最大盈利率分別為和，可能的最大虧損率分別為和，投資人計劃投資金額不超過萬元，要求確保可能的資金虧損不超過萬元.問投資人對甲、乙兩項目各投資多少萬元，才能使可能的盈利最大？

問題4．要將兩種大小不同的鋼板截成、、三種規格，每張鋼板可同時截成三種規格的小鋼板塊數如左下表：

第一種鋼板
第二種鋼板

二元一次不等式表示平面區域.

一般地，二元一次不等式在平面直角坐標系中表示直線某一側的所有點組成的平面區域(半平面)不含邊界線；不等式所表示的平面區域(半平面)包括邊界線．

判定不等式(或)所表示的平面區域時，只要在直線的一側任意取一點，將它的的坐標代入不等式,如果該點的坐標滿足不等式，不等式就表示該點所在一側的平面區域；如果不滿足不等式，就表示這個點所在區域的另一側平面區域。

由幾個不等式組成的不等式組表示的平面區域是各個不等式所表示的平面區域的公共部分．

另外：規律總結：，(視“”為“”,“”為“”)，分別

計算：的符號與“”或“”的積；的符號與“”或“”的積； “左下負,右上正”.

線性規劃問題的圖解法：　

基本概念

名 稱	意　　　　　　　 義
線性約束條件	由的一次不等式(或方程)組成的不等式組，是對x,y的約束條件
目標函數	關于的解析式
線性目標函數	關于的一次解析式
可行解	滿足線性約束條件的解叫做可行解
可行域	所有可行解組成的集合叫做可行域
最優解	使目標函數達到最大值或最小值的可行解
線性規劃問題	求線性目標函數在線性約束條件下的最大值或最小值的問題

用圖解法解決線性規劃問題的一般步驟

①　　 設出所求的未知數；②列出約束條件(即不等式組)；③建立目標函數；

④　　 作出可行域；⑤運用圖解法求出最優解.

解法歸類：圖解法；列表法；待定系數法；調整優值法；打網格線法.

交點定界法.

注意運用線性規劃的思想解題.

(北京)若直線：與直線的交點位于第一象限，

則直線的傾斜角的取值范圍是　

(全國文)直線關于軸對稱的直線方程為

(安徽春)已知直線：，：.若直線與關于對

稱，則的方程為

(上海)直線關于直線對稱的直線方程是　　　　　

(上海文)圓關于直線對稱的圓的方程是

方程表示的直線必經過點

直線關于點對稱的直線方程是

曲線關于直線對稱的曲線方程是　　　　　　　　

，，僅有兩個元素，則實數的范圍是　　　　　　

求經過直線和的交點，且在兩坐標軸上的截距相等的直線方程

已知的頂點為，的平分線所在直線的方程分別是：

與：，求邊所在直線的方程.

已知直線，當變化時所得的直線都經過的定點為　　　　

求證：不論取何實數，直線總通過一定點

求點關于直線：的對稱點的坐標

已知：與，是對稱的兩點，求對稱軸的方程

光線沿直線：射入，遇到直線：反射，求反射光線所在的直線的方程

已知點，，試在直線：上找一點，使 最小，并求出最小值.

問題1．(湖北聯考)一條光線經過點，射在直線：上，

反射后穿過點.求入射光線的方程；求這條光線從點到點的長度.

問題2．求直線：關于直線：對稱的直線的方程.

問題3．根據下列條件，求直線的直線方程

求通過兩條直線和的交點，且到原點距離為；

經過點，且與直線平行；

經過點，且與直線垂直.

問題4．已知方程有一正根而沒有負根，求實數的范圍

若直線：與：的交點在第一象限，求的取值范圍.

　已知定點和直線：

求證：不論取何值，點到直線的距離不大于

點關于軸的對稱點的坐標為；關于軸的對稱點的坐標為；關于的對稱點的坐標為；關于的對稱點的坐標為.

點關于直線的對稱點的坐標的求法：

　設所求的對稱點的坐標為，則的中點一定在直線上.

直線與直線的斜率互為負倒數，即

結論：點關于直線：對稱點為，

其中；曲線：關于直線：的對稱曲線方程為特別地，當，即的斜率為時，點關于直線：對稱點為，即關于直線對稱的點為：，曲線關于的對稱曲線為

直線關于直線的對稱直線方程的求法：

　①到角相等；②在已知直線上去兩點(其中一點可以是交點，若相交)求這兩點關于對稱軸的對稱點，再求過這兩點的直線方程；③軌跡法(相關點法)；④待定系數法，利用對稱軸所在直線上任一點到兩對稱直線的距離相等，…

點關于定點的對稱點為，曲線：關于定點的對稱曲線方程為.

直線系方程：

直線(為常數，參數；為參數，位常數).

過定點的直線系方程為及

與直線平行的直線系方程為()

與直線垂直的直線系方程為

過直線和的交點的直線系的方程為：(不含)

(全國)如果直線與直線平行,那么系數

(全國)兩條直線，垂直的充要條件是：

(北京)“”是“直線與直線 相互垂直”的　　 充分必要條件；　　

　充分而不必要條件；必要而不充分條件； 既不充分也不必要條件.

(京皖春)直線和直線的位置關系是

相交不垂直　　 　 垂直　　 平行　　 重合

(全國Ⅱ)過點且垂直于直線的直線方程為

　(全國Ⅲ)已知過點和的直線與直線平行，則

　的值為　 　　　　　　　　　　　　　　　

　(天津文)“”是“直線平行于直線”的

充分而不必要條件必要而不充分條件充要條件既不充分也不必要條件

　(上海春)直線與直線的夾角為　　　　　　

(浙江)點到直線的距離是

(全國)已知點()到直線：的距離為，則等于

(全國文)已知兩條直線：，：，其中為實數，當這兩條直線的夾角在內變動時，的取值范圍是

　　 　 　　　(，)

已知直線：和直線：，求滿足下列條件的實數的取值范圍或取值：與相交；　　　　　；

∥：　　　；；　　　 ；與重合；　　　

(屆高三北京海淀第一學期期末練習)若直線與直線

平行，則實數的值為或或

(上海)設分別為所對邊長，則直線與直線

的位置關系是：平行重合垂直相交但不垂直

已知，則的最小值是　　　　　　　　

已知：、，且，求證：≥

若兩平行線與之間的距離為，則　　　　

直線在軸和軸上的截距分別為和，直線的方程為，直線與的夾角為，則的值為　　　　　　　　

已知一直線被兩直線：和：截得的

線段長為，且過點，求直線的方程.