
 (
( 屆孝昌二中高三質檢) 在
屆孝昌二中高三質檢) 在 中,已知
中,已知
 ,則
,則 的大小為
的大小為








 (
( 屆高三西安中學
屆高三西安中學 月月考)已知銳角
月月考)已知銳角 中,角
中,角 的對邊分別為
的對邊分別為 ,
,
且 ;
; 求
求 ;
;
 求函數
求函數
 的最大值
的最大值
 已知
已知 的面積
的面積 ,且
,且 ,求
,求 面積的最大值
面積的最大值
問題1.在 中,
中, 分別是三個內角
分別是三個內角 的對邊.如果
的對邊.如果
 且
且 .求證:
.求證: 為直角三角形
為直角三角形
問題2. 求
求
 在
在 中,角
中,角 、
、 、
、 對邊分別為
對邊分別為 、
、 、
、 ,求證:
,求證:
問題3.在 中,
中, 分別是三個內角
分別是三個內角 的對邊,且
的對邊,且
 求角
求角 的度數;
的度數; 若
若 求
求 的值
的值
問題4.( 天津)在
天津)在 中,
中, 所對的邊長分別為
所對的邊長分別為 ,
,
設 滿足條件
滿足條件 和
和 ,求
,求 和
和 的值
的值
利用正余弦定理可以把邊的關系轉化為角的關系,也可以把角的關系轉化為邊的關系 。
 正弦定理:
正弦定理: ,
,
 余弦定理:
余弦定理:
 推論:正余弦定理的邊角互換功能
推論:正余弦定理的邊角互換功能
①  ,
, ,
,
② ,
, ,
,
③  =
= =
=
④
⑤


 三角形中的基本關系式:
三角形中的基本關系式:
 (
( 全國)函數
全國)函數 的最大值是
的最大值是
 已知
已知 求
求 的最大值.
的最大值.
 (
( 全國Ⅱ)在
全國Ⅱ)在 中,已知內角
中,已知內角 ,邊
,邊 .設內角
.設內角 ,周長為
,周長為 .
.
 求函數
求函數 的解析式和定義域;
的解析式和定義域; 求
求 的最大值.
的最大值.
 (
( 重慶)設函數
重慶)設函數 (其中
(其中 ,
, ),且
),且 的圖象在
的圖象在 軸右側的第一個高點的橫坐標為
軸右側的第一個高點的橫坐標為 .
.
(Ⅰ)求 的值;(Ⅱ)如果
的值;(Ⅱ)如果 在區間
在區間 上的最小值為
上的最小值為 ,求
,求 的值.
的值.
 (
( 湖北文)已知函數
湖北文)已知函數 ,
, .
.
(Ⅰ)求 的最大值和最小值;
的最大值和最小值;
(Ⅱ)若不等式 在
在 上恒成立,求實數
上恒成立,求實數 的取值范圍.
的取值范圍.

 在
在 上取得最大值時,
上取得最大值時, 的值是
的值是 







 函數
函數 的最大值
的最大值
 已知
已知 ,則
,則 的最大值是
的最大值是
 當函數
當函數 的最大值為
的最大值為 時,求
時,求 的值.
的值.
問題1. 求函數的最大值和最小值:

 ;
; 

問題2.求下列各函數的最值: 求函數
求函數
 的最大值;
的最大值;


 的最小值.
的最小值.
 的最小值.
的最小值.
問題3. (
( 全國文)函數
全國文)函數 的最大值是
的最大值是

 的最大值是
的最大值是 







 (
(  全國Ⅰ文) 當
全國Ⅰ文) 當 時,函數
時,函數 的最小值為
的最小值為








①配方法;②化為一個角的三角函數;③數形結合法;④換元法;⑤基本不等式法;⑥導數法
① ,設
,設 化為一次函數
化為一次函數 在閉區間
在閉區間 上的最值求之;
上的最值求之;
② ,引入輔助角
,引入輔助角 ,化為
,化為 求解方法同類型①;
求解方法同類型①;
③ ,設
,設 ,化為二次函數
,化為二次函數 在
在 上的最值求之;
上的最值求之;
④ ,設
,設 化為二次函數
化為二次函數 在閉區間
在閉區間 上的最值求之;
上的最值求之;
⑤ ,設
,設 化為
化為 用
用 法求值;當
法求值;當 時,還可用平均值定理求最值;
時,還可用平均值定理求最值;
⑥ 根據正弦函數的有界性,即可分析法求最值,還可“不等式”法或“數形結合”.
根據正弦函數的有界性,即可分析法求最值,還可“不等式”法或“數形結合”.
 (
( 江蘇)已知
江蘇)已知 ,函數
,函數 為奇函數,則
為奇函數,則








 (
( 湖南文)若
湖南文)若 是偶函數,則
是偶函數,則
 (
( 全國Ⅰ)函數
全國Ⅰ)函數 的單調增區間為
的單調增區間為








 (
( 北京)函數
北京)函數
 在
在 上遞增,在
上遞增,在 上遞減
上遞減
 在
在 上遞增,在
上遞增,在 上遞減
上遞減
 在
在 上遞增,在
上遞增,在 上遞減
上遞減
 在
在 上遞增,在
上遞增,在 上遞減
上遞減
 (
( 天津文)設
天津文)設 、
、 ,那么
,那么 是
是 的
的
 充分不必要條件
充分不必要條件 必要不充分條件
必要不充分條件 充要條件
充要條件 既不充分又不必要條件
既不充分又不必要條件
 (
( 安徽)設
安徽)設 ,對于函數
,對于函數 ,下列結論正確的是
,下列結論正確的是
 有最大值無最小值
有最大值無最小值 有最小值無最大值
有最小值無最大值 有最大值且有最小值
有最大值且有最小值 既無最大值又無最小值
既無最大值又無最小值
 (
( 廣東)若函數
廣東)若函數
 ,則
,則 是
是
 最小正周期為
最小正周期為 的奇函數
的奇函數  最小正周期為
最小正周期為 的奇函數
的奇函數
 最小正周期為
最小正周期為 的偶函數
的偶函數  最小正周期為
最小正周期為 的偶函數
的偶函數
 (
( 天津文)設函數
天津文)設函數
 ,則
,則
 在區間
在區間 上是增函數
上是增函數  在區間
在區間 上是減函數
上是減函數
 在區間
在區間 上是增函數
上是增函數  在區間
在區間 上是減函數
上是減函數
 (
( 天津)已知函數
天津)已知函數 、
、 為常數,
為常數, 在
在
處取得最小值,則函數 是
是
 偶函數且它的圖象關于點
偶函數且它的圖象關于點 對稱;
對稱; 偶函數且它的圖象關于點
偶函數且它的圖象關于點 對稱;
對稱;
 奇函數且它的圖象關于點
奇函數且它的圖象關于點 對稱;
對稱; 奇函數且它的圖象關于點
奇函數且它的圖象關于點 對;
對;
 (
( 湖南文)已知函數
湖南文)已知函數
求:(Ⅰ)函數 的最小正周期;(Ⅱ)函數
的最小正周期;(Ⅱ)函數 的單調增區間.
的單調增區間.
 (
( 湖南)已知函數
湖南)已知函數 ,
, .
.
(Ⅰ)設 是函數
是函數 圖象的一條對稱軸,求
圖象的一條對稱軸,求 的值.
的值.
(Ⅱ)求函數 的單調遞增區間.
的單調遞增區間.
 (
( 遼寧)已知函數
遼寧)已知函數 ,
,
(其中 ,
, )(Ⅰ)求函數
)(Ⅰ)求函數 的值域;
的值域;
(Ⅱ)若對任意的 ,函數
,函數 ,
, 的圖象與直線
的圖象與直線 有且僅有兩個不同的交點,試確定
有且僅有兩個不同的交點,試確定 的值(不必證明),并求函數
的值(不必證明),并求函數 的單調增區間.
的單調增區間.
 (
( 江西)如圖,函數
江西)如圖,函數
 的圖象與
的圖象與 軸相交于點
軸相交于點 ,且該函數的最小正周期為
,且該函數的最小正周期為 .
. 求
求 和
和 的值;
的值;
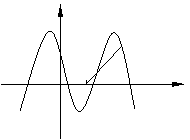
 已知點
已知點 ,點
,點 是該函數圖象上一點,點
是該函數圖象上一點,點 是
是 的中點,當
的中點,當 ,
, 時,求
時,求 的值.
的值.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com