
 設
設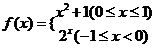 ,則
,則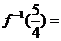
 設
設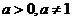 ,函數(shù)
,函數(shù) 的反函數(shù)和
的反函數(shù)和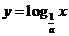 的反函數(shù)的圖象關于
的反函數(shù)的圖象關于

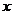 軸對稱
軸對稱

 軸對稱
軸對稱 
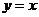 軸對稱
軸對稱  原點對稱
原點對稱
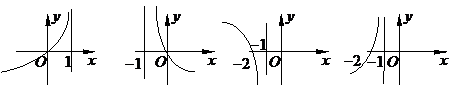
 已知函數(shù)
已知函數(shù)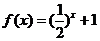 ,則
,則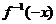 的圖象只可能是
的圖象只可能是




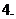 若
若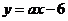 與
與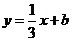 的圖象關于直線
的圖象關于直線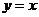 對稱,且點
對稱,且點 在指數(shù)函數(shù)
在指數(shù)函數(shù)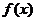 的
的
圖象上,則
 設函數(shù)
設函數(shù) 滿足
滿足 ,則
,則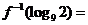
 己知:函數(shù)
己知:函數(shù)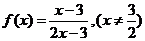 ,若
,若 的圖像是
的圖像是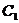 ,它關于直線
,它關于直線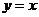 對稱
對稱
圖像是 關于原點對稱的圖像為
關于原點對稱的圖像為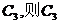 對應的函數(shù)解析式是____________
對應的函數(shù)解析式是____________
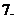 若
若 既在
既在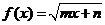 的圖象上,又在它反函數(shù)圖象上,求
的圖象上,又在它反函數(shù)圖象上,求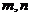 的值.
的值.
 (
( 湖南文)設
湖南文)設 是函數(shù)
是函數(shù) 的反函數(shù),則下面不等式中恒成立的是
的反函數(shù),則下面不等式中恒成立的是

 ≤
≤

 ≤
≤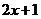

 ≥
≥

 ≥
≥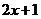
 已知函數(shù)
已知函數(shù)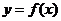 的反函數(shù)為
的反函數(shù)為 ,求函數(shù)
,求函數(shù)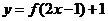 的反函數(shù).
的反函數(shù).
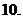 已知
已知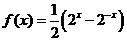 的反函數(shù)為
的反函數(shù)為 ,則不等式
,則不等式 的解集為
的解集為
 已知函數(shù)
已知函數(shù)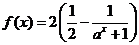 (
( ,且
,且 )
)
 求函數(shù)
求函數(shù)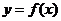 的反函數(shù)
的反函數(shù) ;
;
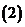 判定
判定 的單調(diào)性;
的單調(diào)性; 解不等式
解不等式
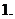 要使
要使 (
(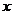 ≥
≥ )有反函數(shù),則
)有反函數(shù),則 的最小值為
的最小值為
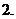 設
設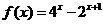 ,則
,則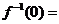
 (
( 新課程)函數(shù)
新課程)函數(shù) 圖象與其反函數(shù)圖象的交點坐標為
圖象與其反函數(shù)圖象的交點坐標為
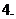 若函數(shù)
若函數(shù)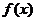 的圖象經(jīng)過點
的圖象經(jīng)過點 ,則函數(shù)
,則函數(shù) 的反函數(shù)圖象必經(jīng)過
的反函數(shù)圖象必經(jīng)過








 (
(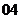 全國Ⅰ)已知函數(shù)
全國Ⅰ)已知函數(shù)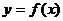 是奇函數(shù),當
是奇函數(shù),當 時,
時, ,設
,設 的反函數(shù)是
的反函數(shù)是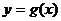 ,則
,則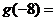
問題1. 求下列函數(shù)的反函數(shù):
 (
(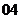 全國)
全國)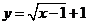 (
(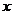 ≥
≥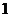 );
);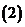 (
( 上海春)
上海春) 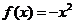 (
(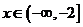 )
)
 (
(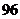 上海)
上海)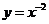 (
(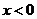 );
);
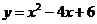 (
(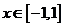 )
)
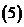
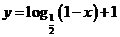 (
( );
); 
 (
(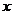 ≤
≤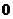 );
);
 (
( 安徽)
安徽)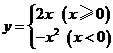 .
.
問題2.
 (
( 北京文)已知函數(shù)
北京文)已知函數(shù) 的反函數(shù)的圖象經(jīng)過點
的反函數(shù)的圖象經(jīng)過點 ,則
,則
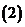 已知
已知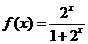
 ,求
,求 的值
的值
問題3. (
( 遼寧)與方程
遼寧)與方程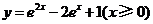 的曲線關于直線
的曲線關于直線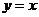 對稱的
對稱的
曲線方程為 


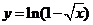

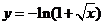

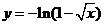
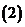 函數(shù)
函數(shù)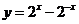 的反函數(shù)
的反函數(shù)
 是奇函數(shù),且在
是奇函數(shù),且在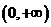 是減函數(shù)
是減函數(shù) 是偶函數(shù),且在
是偶函數(shù),且在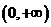 是減函數(shù)
是減函數(shù)
 是奇函數(shù),且在
是奇函數(shù),且在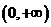 是增函數(shù)
是增函數(shù) 是偶函數(shù),且在
是偶函數(shù),且在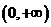 是增函數(shù)
是增函數(shù)
 (
( 全國)設函數(shù)
全國)設函數(shù)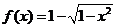 (
(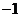 ≤
≤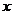 ≤
≤ ),則函數(shù)
),則函數(shù) 的圖像是
的圖像是

問題4. 函數(shù)
函數(shù)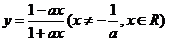 的圖象關于
的圖象關于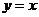 對稱,求
對稱,求 的值.
的值.
 設函數(shù)
設函數(shù) ,又函數(shù)
,又函數(shù)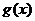 與
與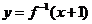 的圖象關于
的圖象關于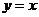 對稱,求
對稱,求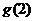 .
.
問題5. 已知
已知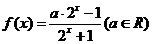 ,是
,是 上的奇函數(shù).
上的奇函數(shù). 求
求 的值,
的值,
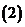 求
求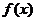 的反函數(shù),
的反函數(shù), 對任意的
對任意的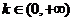 解不等式
解不等式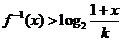 .
.
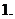 求反函數(shù)的一般步驟:
求反函數(shù)的一般步驟: 求原函數(shù)的值域;
求原函數(shù)的值域;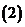 反解,由
反解,由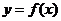 解出
解出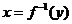 ;
;
 寫出反函數(shù)的解析式(互換
寫出反函數(shù)的解析式(互換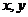 ),并注明反函數(shù)的定義域(即原函數(shù)的值域).
),并注明反函數(shù)的定義域(即原函數(shù)的值域).
注:析分段函數(shù)的反函數(shù)可以分別求出各段函數(shù)的反函數(shù)再合成.
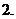 若函數(shù)
若函數(shù)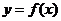 與
與 互為反函數(shù),且
互為反函數(shù),且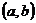 在
在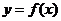 的圖像上,則
的圖像上,則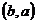 在
在 圖像上。
圖像上。
 若函數(shù)
若函數(shù)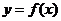 與
與 互為反函數(shù),若
互為反函數(shù),若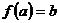 ,則
,則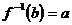 .
.
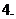 求證一個函數(shù)
求證一個函數(shù)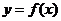 的圖象關于
的圖象關于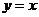 成軸對稱圖形,只須證明
成軸對稱圖形,只須證明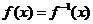 .
.
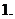 設函數(shù)
設函數(shù)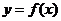 的定義域為
的定義域為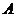 ,值域為
,值域為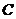 ,由
,由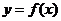 求出
求出 .如果對于
.如果對于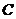 中
每個
中
每個 值,在
值,在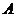 中都有唯一的值和它對應,那么
中都有唯一的值和它對應,那么 為以
為以 為自變量的函數(shù),叫做
為自變量的函數(shù),叫做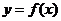 的反函數(shù),記作
的反函數(shù),記作 ,(
,( )
)
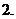 反函數(shù)存在的條件:從定義域到值域上的一一映射確定的函數(shù)才有反函數(shù);
反函數(shù)存在的條件:從定義域到值域上的一一映射確定的函數(shù)才有反函數(shù);
 反函數(shù)的定義域、值域上分別是原函數(shù)的值域、定義域,若
反函數(shù)的定義域、值域上分別是原函數(shù)的值域、定義域,若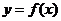 與
與
互為反函數(shù),函數(shù)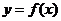 的定義域為
的定義域為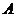 、值域為
、值域為 ,則
,則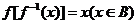 ,
, ;
;
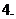 互為反函數(shù)的兩個函數(shù)具有相同的單調(diào)性,它們的圖象關于
互為反函數(shù)的兩個函數(shù)具有相同的單調(diào)性,它們的圖象關于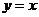 對稱.
對稱.
 一些結(jié)論:
一些結(jié)論: 定義域上的單調(diào)函數(shù)必有反函數(shù);
定義域上的單調(diào)函數(shù)必有反函數(shù);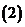 奇函數(shù)若存在反函數(shù),則其反函數(shù)也是奇函數(shù);
奇函數(shù)若存在反函數(shù),則其反函數(shù)也是奇函數(shù); 定義域為非單元素集的偶函數(shù)不存在反函數(shù).
定義域為非單元素集的偶函數(shù)不存在反函數(shù). 周期函數(shù)在整個定義域內(nèi)不存在反函數(shù).
周期函數(shù)在整個定義域內(nèi)不存在反函數(shù).
 (
( 福建)
福建) 是定義在
是定義在 上的以
上的以 為周期的奇函數(shù),且
為周期的奇函數(shù),且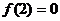 在區(qū)間
在區(qū)間 內(nèi)解
內(nèi)解
的個數(shù)的最小值是

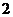
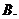


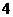
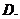
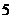
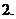 (
(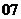 安徽)定義在
安徽)定義在 上的函數(shù)
上的函數(shù) 既是奇函數(shù),又是周期函數(shù),
既是奇函數(shù),又是周期函數(shù), 是它的一個正周期.
是它的一個正周期.
若將方程 在閉區(qū)間
在閉區(qū)間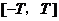 上的根的個數(shù)記為
上的根的個數(shù)記為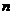 ,則
,則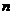 可能為
可能為



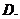
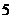
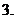 (
(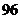 全國)已知函數(shù)
全國)已知函數(shù) 為
為 上的奇函數(shù),且滿足
上的奇函數(shù),且滿足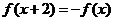 ,
,
當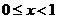 時,
時,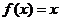 ,則
,則 等于( )
等于( )


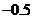

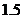
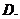
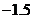
 (
( 安徽)函數(shù)
安徽)函數(shù) 對于任意實數(shù)
對于任意實數(shù)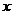 滿足條件
滿足條件 ,若
,若 ,
,
則
 (
( 福建文)已知
福建文)已知 是周期為
是周期為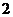 的奇函數(shù),當
的奇函數(shù),當 時,
時,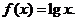
設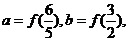
 則
則

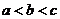
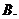
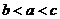

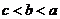
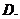
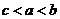
 (
( 天津)定義在
天津)定義在 上的函數(shù)
上的函數(shù) 既是偶函數(shù)又是周期函數(shù),若
既是偶函數(shù)又是周期函數(shù),若 的最小正周期
的最小正周期
是 ,且當
,且當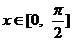 時,
時,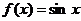 ,則
,則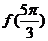 的值為
的值為

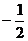
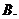
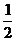


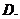
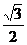
 (
( 天津)設
天津)設 是定義在
是定義在 上的奇函數(shù),且
上的奇函數(shù),且 的圖象關于直線
的圖象關于直線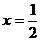
對稱,則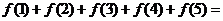
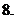 (
( 廣東)設函數(shù)
廣東)設函數(shù) 在
在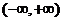 上滿足
上滿足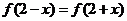 ,
,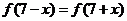 ,且在閉區(qū)間
,且在閉區(qū)間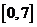 上,只有
上,只有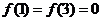 .
.
(Ⅰ)試判斷函數(shù)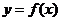 的奇偶性;
的奇偶性;
(Ⅱ)試求方程 在閉區(qū)間
在閉區(qū)間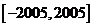 上的根的個數(shù),并證明你的結(jié)論
上的根的個數(shù),并證明你的結(jié)論
 已知函數(shù)
已知函數(shù) 是以
是以 為周期的周期函數(shù),且當
為周期的周期函數(shù),且當 時,
時,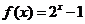 ,則
,則
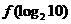 的值為
的值為 
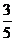
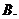


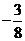
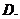
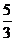
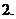 設偶函數(shù)
設偶函數(shù) 對任意
對任意 ,都有
,都有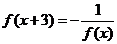 ,且當
,且當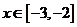 時,
時,
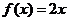 ,則
,則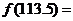


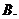
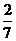

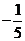
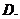
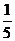
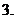 設函數(shù)
設函數(shù) 是定義在
是定義在 上的奇函數(shù),對于任意的
上的奇函數(shù),對于任意的 ,都有
,都有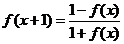 ,
,
當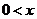 ≤
≤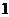 時,
時,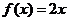 ,則
,則

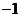

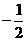
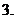 已知
已知 是定義在實數(shù)集
是定義在實數(shù)集 上的函數(shù),滿足
上的函數(shù),滿足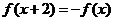 ,且
,且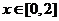 時,
時,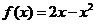 .
.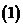 求
求 時,
時, 的表達式;
的表達式; 證明
證明 是
是 上的奇函數(shù).
上的奇函數(shù).
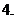 (
( 朝陽模擬)已知函數(shù)
朝陽模擬)已知函數(shù) 的圖象關于點
的圖象關于點 對稱,且滿足
對稱,且滿足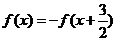 ,又
,又 ,
,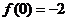 ,求
,求 …
… 的值
的值
 (
(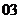 北京春)若存在常數(shù)
北京春)若存在常數(shù)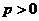 ,使得函數(shù)
,使得函數(shù) 滿足
滿足
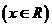 ,
,
 的一個正周期為
的一個正周期為
 設函數(shù)
設函數(shù) (
(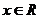 )是以
)是以 為周期的奇函數(shù),且
為周期的奇函數(shù),且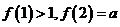 ,則
,則



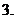 函數(shù)
函數(shù) 既是定義域為
既是定義域為 的偶函數(shù),又是以
的偶函數(shù),又是以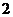 為周期的周期函數(shù),若
為周期的周期函數(shù),若 在
在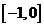 上
上
是減函數(shù),那么 在
在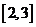 上是
上是
 增函數(shù)
增函數(shù) 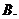 減函數(shù)
減函數(shù)  先增后減函數(shù)
先增后減函數(shù) 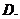 先減后增函數(shù)
先減后增函數(shù)
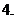 設
設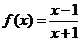 ,記
,記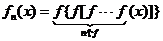 ,則
,則
問題1.( 山東)已知定義在
山東)已知定義在 上的奇函數(shù)
上的奇函數(shù) 滿足
滿足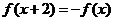 ,則
,則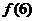 的值為
的值為 
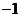
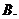
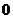

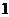
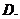
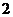
 問題2.
問題2.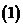 (
(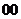 上海) 設
上海) 設 的最小正周期
的最小正周期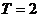 且
且 為偶函數(shù),
為偶函數(shù),
它在區(qū)間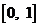 上的圖象如右圖所示的線段
上的圖象如右圖所示的線段 ,則在區(qū)間
,則在區(qū)間 上,
上,
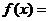
 已知函數(shù)
已知函數(shù) 是周期為
是周期為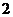 的函數(shù),當
的函數(shù),當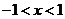 時,
時,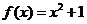 ,
,
當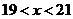 時,
時, 的解析式是
的解析式是
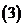
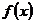 是定義在
是定義在 上的以
上的以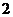 為周期的函數(shù),對
為周期的函數(shù),對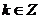 ,用
,用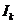 表示區(qū)間
表示區(qū)間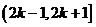 ,
,
已知當 時,
時, ,求
,求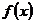 在
在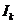 上的解析式。
上的解析式。
問題3.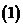 (
( 福建)定義在
福建)定義在 上的函數(shù)
上的函數(shù)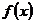 滿足
滿足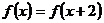 ,當
,當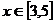 時,
時,
 ,則
,則 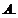
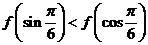 ;
; 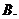
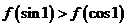 ;
;
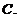
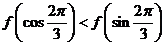
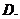

 (
( 天津文) 設
天津文) 設 是定義在
是定義在 上以
上以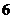 為周期的函數(shù),
為周期的函數(shù), 在
在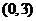 內(nèi)單調(diào)遞減,
內(nèi)單調(diào)遞減,
且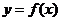 的圖像關于直線
的圖像關于直線 對稱,則下面正確的結(jié)論是
對稱,則下面正確的結(jié)論是
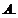
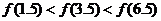
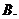

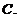
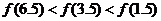
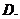

問題4.定義在 上的函數(shù)
上的函數(shù)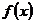 ,對任意
,對任意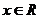 ,有
,有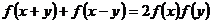 ,且
,且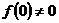 ,
,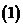 求證:
求證: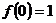 ;
; 判斷
判斷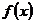 的奇偶性;
的奇偶性;
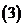 若存在非零常數(shù)
若存在非零常數(shù)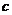 ,使
,使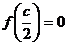 ,①證明對任意
,①證明對任意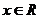 都有
都有 成立;
成立;
②函數(shù)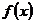 是不是周期函數(shù),為什么?
是不是周期函數(shù),為什么?
問題5.(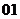 全國)設
全國)設 是定義在
是定義在 上的偶函數(shù),其圖象關于直線
上的偶函數(shù),其圖象關于直線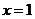 對稱,對任
對稱,對任
意的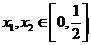 ,都有
,都有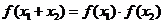 .
.
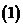 設
設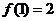 ,求
,求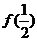 、
、 ;
; 證明:
證明: 是周期函數(shù).
是周期函數(shù).
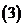 記
記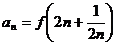 ,求
,求 .
.
 判斷一個函數(shù)是否是周期函數(shù)要抓住兩點:一是對定義域中任意的
判斷一個函數(shù)是否是周期函數(shù)要抓住兩點:一是對定義域中任意的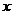 恒有
恒有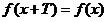 ;
;
二是能找到適合這一等式的非零常數(shù) ,一般來說,周期函數(shù)的定義域均為無限集.
,一般來說,周期函數(shù)的定義域均為無限集.
 解決周期函數(shù)問題時,要注意靈活運用以上結(jié)論,同時要重視數(shù)形結(jié)合思想方法的運用,還要注意根據(jù)所要解決的問題的特征來進行賦值。
解決周期函數(shù)問題時,要注意靈活運用以上結(jié)論,同時要重視數(shù)形結(jié)合思想方法的運用,還要注意根據(jù)所要解決的問題的特征來進行賦值。
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com