
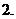 集合中元素的
集合中元素的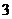 個性質(zhì),集合的
個性質(zhì),集合的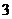 種表示方法;
種表示方法;
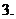 若有限集
若有限集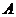 有
有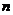 個元素,則
個元素,則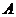 的子集有
的子集有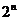 個,真子集有
個,真子集有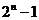 ,非空子集有
,非空子集有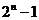 個,非空真子集有
個,非空真子集有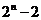 個.
個.
 空集是任何集合的子集,空集是任何非空集合的真子集.
空集是任何集合的子集,空集是任何非空集合的真子集.
 若
若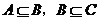 ,則
,則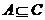
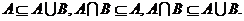
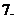
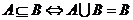 ;
;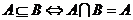 .
.
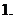 (
(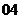 北京春) 某服裝廠生產(chǎn)一種服裝,每件服裝的成本為
北京春) 某服裝廠生產(chǎn)一種服裝,每件服裝的成本為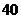 元,出廠單價定為
元,出廠單價定為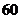 元。該廠為鼓勵銷售商訂購,決定當(dāng)一次訂購量超過
元。該廠為鼓勵銷售商訂購,決定當(dāng)一次訂購量超過 件時,每多訂購一件,訂購的全部服裝的出廠單價就降低
件時,每多訂購一件,訂購的全部服裝的出廠單價就降低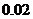 元。根據(jù)市場調(diào)查,銷售商一次訂購量不會超過
元。根據(jù)市場調(diào)查,銷售商一次訂購量不會超過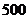 件。
件。
(Ⅰ)設(shè)一次訂購量為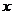 件,服裝的實際出廠單價為
件,服裝的實際出廠單價為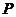 元,寫出函數(shù)
元,寫出函數(shù)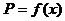 的表達式;
的表達式;
(Ⅱ)當(dāng)銷售商一次訂購了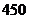 件服裝時,該服裝廠獲得的利潤是多少元?
件服裝時,該服裝廠獲得的利潤是多少元?
(服裝廠售出一件服裝的利潤=實際出廠單價-成本)
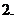 (
(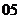 湖南文)某公司在甲、乙兩地銷售一種品牌車,利潤(單位:萬元)分別為
湖南文)某公司在甲、乙兩地銷售一種品牌車,利潤(單位:萬元)分別為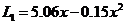 和
和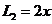 ,其中
,其中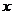 為銷售量(單位:輛).若該公司在這兩地共銷售
為銷售量(單位:輛).若該公司在這兩地共銷售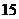 輛車,則能獲得的最大利潤為
輛車,則能獲得的最大利潤為
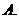
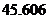
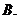
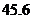
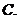
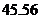
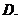
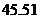
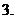
 (
(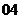 上海)某單位用木料制作如圖所示的框架, 框架的下部是邊長
上海)某單位用木料制作如圖所示的框架, 框架的下部是邊長
分別為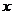 、
、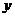 (單位:
(單位: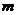 )的矩形.上部是等腰直角三角形. 要求
)的矩形.上部是等腰直角三角形. 要求
框架圍成的總面積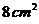 . 問
. 問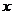 、
、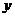 分別為多少(精確到
分別為多少(精確到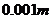 )
)
時用料最省?
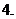 (
(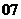 湖北文)某商品每件成本
湖北文)某商品每件成本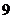 元,售價為
元,售價為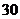 元,每星期賣出
元,每星期賣出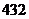 件,如果降低價格,銷售量可以增加,且每星期多賣出的商品件數(shù)與商品單價的降低值
件,如果降低價格,銷售量可以增加,且每星期多賣出的商品件數(shù)與商品單價的降低值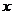 (單位:元,
(單位:元,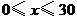 )的平方成正比,已知商品單價降低
)的平方成正比,已知商品單價降低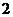 元時,一星期多賣出
元時,一星期多賣出 件.
件.
(Ⅰ)將一個星期的商品銷售利潤表示成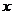 的函數(shù);
的函數(shù);
(Ⅱ)如何定價才能使一個星期的商品銷售利潤最大?
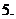 (
( 湖北文)為了預(yù)防流感,某學(xué)校對教室用藥熏
湖北文)為了預(yù)防流感,某學(xué)校對教室用藥熏
消毒法進行消毒.已知藥物釋放過程中,室內(nèi)每立方米
空氣中的含藥量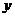 (毫克)與時間
(毫克)與時間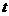 (小時)成正比;
(小時)成正比;
藥物釋放完畢后,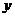 與
與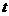 的函數(shù)關(guān)系式為
的函數(shù)關(guān)系式為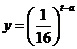
(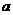 為常數(shù)),如圖所示,根據(jù)圖中提供的信息,
為常數(shù)),如圖所示,根據(jù)圖中提供的信息,
回答下列問題:
(Ⅰ)從藥物釋放開始,每立方米空氣中的含藥量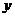
(毫克)與時間 (小時)之間的函數(shù)關(guān)系式為
(小時)之間的函數(shù)關(guān)系式為
(Ⅱ)據(jù)測定,當(dāng)空氣中每立方米的含藥量降低到
 毫克以下時,學(xué)生方可進教室,那么從藥物釋放開始,至少需要經(jīng)過 小時后,學(xué)生才能回到教室.
毫克以下時,學(xué)生方可進教室,那么從藥物釋放開始,至少需要經(jīng)過 小時后,學(xué)生才能回到教室.
問題1.( 全國文)某村計劃建造一個室內(nèi)面積為
全國文)某村計劃建造一個室內(nèi)面積為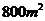 的矩形蔬菜溫室。在溫室內(nèi),沿左、右兩側(cè)與后側(cè)內(nèi)墻各保留
的矩形蔬菜溫室。在溫室內(nèi),沿左、右兩側(cè)與后側(cè)內(nèi)墻各保留 寬的通道,沿前側(cè)內(nèi)墻保留
寬的通道,沿前側(cè)內(nèi)墻保留 寬的空地。當(dāng)矩形溫室的邊長各為多少時,蔬菜的種植面積最大?最大種植面積是多少?
寬的空地。當(dāng)矩形溫室的邊長各為多少時,蔬菜的種植面積最大?最大種植面積是多少?
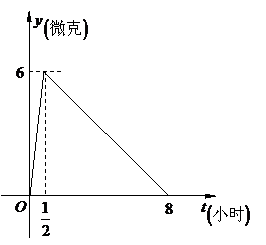 問題2.某醫(yī)藥研究所開發(fā)一種新藥,如果成人按
問題2.某醫(yī)藥研究所開發(fā)一種新藥,如果成人按
規(guī)定的劑量服用,據(jù)監(jiān)測,服藥后每毫升血液中的含藥
量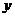 與時間
與時間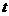 之間近似滿足如圖所示的曲線:
之間近似滿足如圖所示的曲線:
 寫出服藥后
寫出服藥后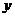 與
與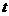 之間的函數(shù)關(guān)系式;
之間的函數(shù)關(guān)系式;
 據(jù)測定:每毫升血液中含藥量不少于
據(jù)測定:每毫升血液中含藥量不少于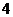 微克時
微克時
治療疾病有效,假若某病人一天中第一次服藥時間
為 ,問一天中怎樣安排服藥的時間、次數(shù)、
,問一天中怎樣安排服藥的時間、次數(shù)、
效果最佳?
 問題3.(
問題3.( 全國Ⅲ文)用長為
全國Ⅲ文)用長為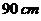 寬為
寬為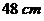 的長方形鐵皮做一個無蓋的容器,先在四角分別截去一個小正方形,然后把四邊翻轉(zhuǎn)
的長方形鐵皮做一個無蓋的容器,先在四角分別截去一個小正方形,然后把四邊翻轉(zhuǎn)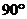 角,再焊接而成(如圖),問該容器的高為多少時,容器的容積最大?最大容積是多少?
角,再焊接而成(如圖),問該容器的高為多少時,容器的容積最大?最大容積是多少?
問題4.(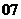 山東文)本公司計劃
山東文)本公司計劃 年在甲、乙兩個電視臺做總時間不超過
年在甲、乙兩個電視臺做總時間不超過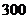 分鐘的廣告,廣告總費用不超過
分鐘的廣告,廣告總費用不超過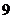 萬元,甲、乙電視臺的廣告收費標(biāo)準(zhǔn)分別為
萬元,甲、乙電視臺的廣告收費標(biāo)準(zhǔn)分別為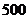 元/分鐘和
元/分鐘和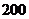 元/分鐘,規(guī)定甲、乙兩個電視臺為該公司所做的每分鐘廣告,能給公司事來的收益分別為
元/分鐘,規(guī)定甲、乙兩個電視臺為該公司所做的每分鐘廣告,能給公司事來的收益分別為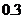 萬元和
萬元和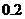 萬元.問該公司如何分配在甲、乙兩個電視臺的廣告時間,才能使公司的收益最大,最大收益是多少萬元?
萬元.問該公司如何分配在甲、乙兩個電視臺的廣告時間,才能使公司的收益最大,最大收益是多少萬元?
問題5.(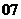 福建)某分公司經(jīng)銷某種品牌產(chǎn)品,每件產(chǎn)品的成本為
福建)某分公司經(jīng)銷某種品牌產(chǎn)品,每件產(chǎn)品的成本為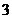 元,并且每件產(chǎn)品需向總公司交
元,并且每件產(chǎn)品需向總公司交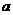 元(
元(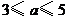 )的管理費,預(yù)計當(dāng)每件產(chǎn)品的售價為
)的管理費,預(yù)計當(dāng)每件產(chǎn)品的售價為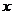 元(
元(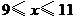 )時,一年的銷售量為
)時,一年的銷售量為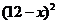 萬件.
萬件.
(Ⅰ)求分公司一年的利潤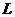 (萬元)與每件產(chǎn)品的售價
(萬元)與每件產(chǎn)品的售價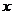 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(Ⅱ)當(dāng)每件產(chǎn)品的售價為多少元時,分公司一年的利潤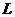 最大,并求出
最大,并求出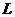 的最大值
的最大值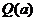 .
.
解數(shù)學(xué)應(yīng)用題的一般步驟為: 審題;
審題; 建模;
建模; 求解;
求解; 作答.
作答.
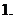 函數(shù)定義域、圖象、單調(diào)性質(zhì)等知識;
函數(shù)定義域、圖象、單調(diào)性質(zhì)等知識;
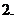 函數(shù)的值域、最值;解不等式等知識。
函數(shù)的值域、最值;解不等式等知識。
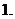 (
(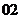 新課程)已知
新課程)已知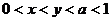 ,則有
,則有

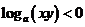

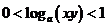

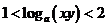

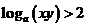
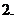 (
(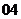 江蘇)若函數(shù)
江蘇)若函數(shù)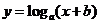
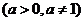 的圖象過兩點
的圖象過兩點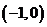 和
和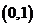 ,則
,則

 ,
,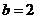

 ,
,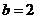

 ,
,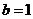

 ,
,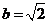
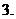 (
(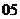 全國Ⅰ)若正整數(shù)
全國Ⅰ)若正整數(shù)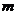 滿足
滿足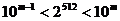 ,則
,則

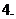 (
( 全國Ⅰ)設(shè)
全國Ⅰ)設(shè)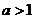 ,函數(shù)
,函數(shù)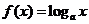 在區(qū)間
在區(qū)間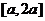 上的最大值與最小值之差為
上的最大值與最小值之差為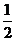 ,則
,則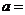

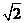



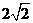

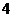
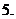 (
(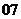 全國Ⅱ)下列四個數(shù)中最大的是( )
全國Ⅱ)下列四個數(shù)中最大的是( )

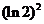

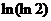

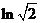

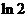
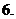 (
( 天津文)設(shè)
天津文)設(shè)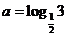 ,
,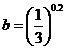 ,
,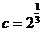 ,則( )
,則( )

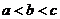

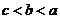

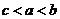

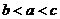
 (
( 天津文)若函數(shù)
天津文)若函數(shù)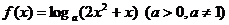 在區(qū)間
在區(qū)間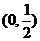 內(nèi)恒有
內(nèi)恒有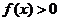 ,則
,則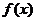 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為

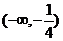

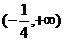

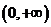

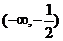
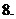 (
(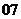 天津)設(shè)
天津)設(shè)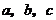 均為正數(shù),且
均為正數(shù),且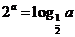 ,
,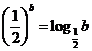 ,
,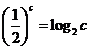 .則
.則
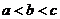

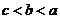

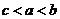

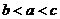
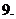 (
(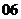 浙江)已知
浙江)已知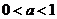 ,
,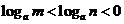 ,則
,則

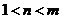

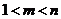

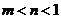

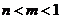
 (
( 遼寧文)設(shè)
遼寧文)設(shè)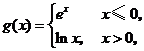 則
則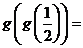
 (
( 遼寧文)方程
遼寧文)方程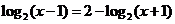 的解為
的解為
 (
( 重慶)函數(shù)
重慶)函數(shù)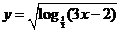 的定義域是
的定義域是 
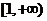

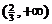

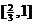

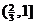
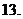 (
( 福建)已知函數(shù)
福建)已知函數(shù)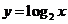 的反函數(shù)是
的反函數(shù)是 ,則函數(shù)
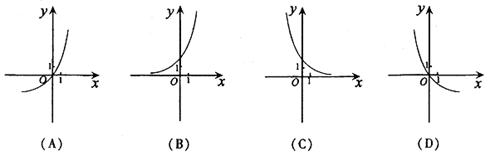
,則函數(shù)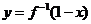 的圖象是
的圖象是
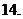 (
( 四川)函數(shù)
四川)函數(shù)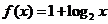 與
與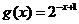 在同一直角坐標(biāo)系下的圖象大致是
在同一直角坐標(biāo)系下的圖象大致是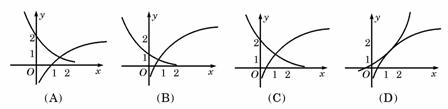
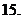 (
(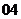 上海文)若函數(shù)
上海文)若函數(shù)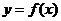 的圖象與函數(shù)
的圖象與函數(shù)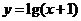 的圖象關(guān)于直線
的圖象關(guān)于直線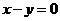 對稱,則
對稱,則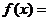

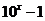

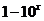

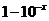

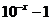
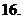 (
(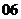 天津文)設(shè)
天津文)設(shè) ,
,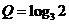 ,
,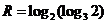 ,則
,則



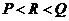

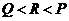

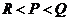
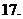 (
( 浙江文)已知
浙江文)已知 ,則
,則

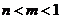

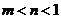

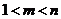

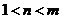
 (
( 浙江)已知
浙江)已知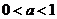 ,
,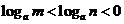 ,則
,則

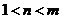

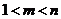

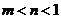

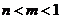
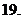 (
( 遼寧)若
遼寧)若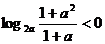 ,則
,則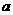 的取值范圍是
的取值范圍是

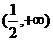

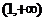

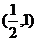

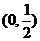
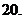 (
(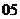 全國Ⅲ)若
全國Ⅲ)若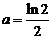 ,
,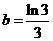 ,
,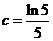 ,則
,則

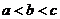

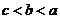

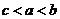

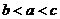
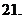 (
( 山東文)下列大小關(guān)系正確的是
山東文)下列大小關(guān)系正確的是

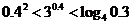 ;
; 
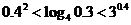 ;
;

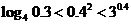 ;
; 
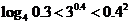
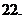 (
(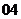 廣東)函數(shù)
廣東)函數(shù)
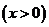 的反函數(shù)
的反函數(shù)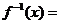
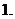 已知函數(shù)
已知函數(shù) ,若
,若 ,則
,則 、
、 、
、 從小到大依次為
從小到大依次為
(注: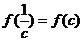 )
)
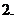 函數(shù)
函數(shù)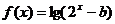 (
(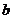 為常數(shù)),若
為常數(shù)),若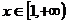 時,
時,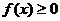 恒成立,則
恒成立,則

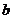 ≤
≤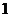

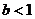
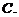
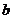 ≥
≥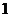

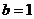
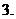
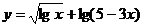 的定義域為
;
的定義域為
;
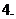
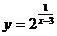 的值域為
;
的值域為
;
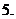
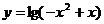 的遞增區(qū)間為
,值域為
的遞增區(qū)間為
,值域為
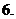
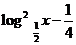 ≤
≤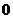 ,則
,則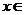
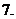 函數(shù)
函數(shù)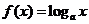
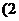 ≤
≤ ≤
≤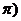 的最大值比最小值大
的最大值比最小值大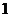 ,則
,則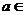
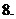 若
若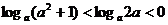 ,則
,則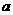 的取值范圍是
的取值范圍是

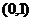

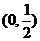
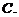
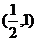

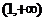
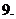 已知
已知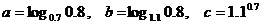 ,則
,則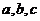 的大小關(guān)系是
的大小關(guān)系是

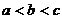



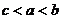

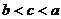
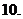 (
( 天津河西區(qū)模擬)若函數(shù)
天津河西區(qū)模擬)若函數(shù)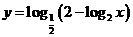 的值域是
的值域是




 已知函數(shù)
已知函數(shù)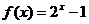 的反函數(shù)為
的反函數(shù)為
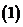 若
若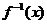 ≤
≤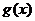 ,求
,求 的取值范圍
的取值范圍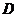 ;
;
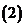 設(shè)
設(shè)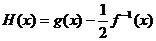 ,當(dāng)
,當(dāng)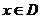 時,求函數(shù)
時,求函數(shù)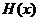 的值域
的值域
 (
(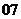 鄭州質(zhì)檢)已知函數(shù)
鄭州質(zhì)檢)已知函數(shù)

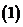 試判斷
試判斷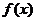 的奇偶性;
的奇偶性;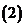 解不等式
解不等式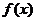 ≥
≥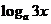
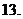 (
(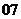 湖北八校聯(lián)考)設(shè)
湖北八校聯(lián)考)設(shè)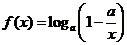 (
(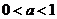 ).
).
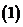 證明:
證明: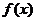 是
是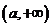 上的減函數(shù);
上的減函數(shù);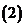 解不等式
解不等式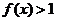
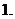 函數(shù)
函數(shù)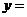
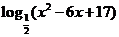 的值域是
的值域是

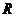

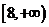

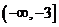

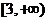
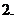 (
(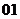 全國)若定義在區(qū)間
全國)若定義在區(qū)間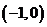 內(nèi)的函數(shù)
內(nèi)的函數(shù)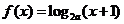 滿足
滿足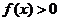 ,則
,則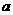 的
的
取值范圍是

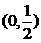

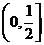

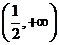

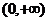
問題1.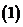 (
( 上海)若
上海)若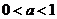 ,則函數(shù)
,則函數(shù)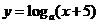 的圖象不經(jīng)過
的圖象不經(jīng)過
 第一象限
第一象限  第二象限
第二象限  第三象限
第三象限  第四象限
第四象限
( 安徽文)設(shè)
安徽文)設(shè)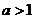 ,且
,且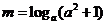 ,
,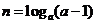 ,
,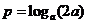 ,則
,則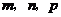 的大小關(guān)系為
的大小關(guān)系為

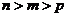

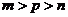

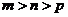

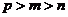
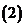 若函數(shù)
若函數(shù)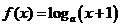 (
(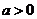 ,
,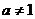 )的定義域和值域都是
)的定義域和值域都是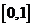 ,則
,則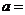

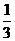

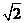

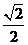


 若
若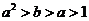 ,則
,則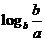 ,
,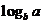 ,
,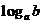 從小到大依次為
從小到大依次為
問題2.求下列函數(shù)的值域 :
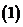
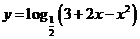 ;
;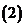
 (
( ≥
≥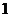 )
)
問題3.  (
( 江蘇)不等式
江蘇)不等式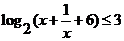 的解集為
的解集為
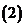 若不等式
若不等式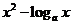 ≤
≤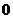 在
在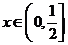 內(nèi)恒成立,則
內(nèi)恒成立,則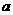 的取值范圍是
的取值范圍是

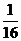 ≤
≤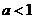

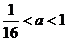

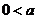 ≤
≤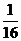

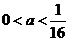
問題4.已知函數(shù)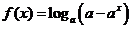 (
(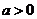 且
且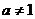 )
)
 求
求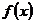 的定義域,值域;
的定義域,值域;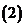 求證該函數(shù)的圖象關(guān)于直線
求證該函數(shù)的圖象關(guān)于直線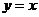 對稱;
對稱;
 解不等式
解不等式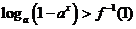
問題5. 設(shè)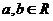 且
且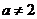 ,定義在區(qū)間
,定義在區(qū)間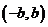 內(nèi)的函數(shù)
內(nèi)的函數(shù)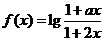 是奇函數(shù).
是奇函數(shù).
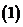 求
求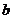 的取值范圍;
的取值范圍;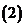 討論函數(shù)
討論函數(shù)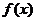 的單調(diào)性.
的單調(diào)性.
 解決與對數(shù)函數(shù)有關(guān)的問題,要特別重視定義域;
解決與對數(shù)函數(shù)有關(guān)的問題,要特別重視定義域;
 解決對數(shù)不等式、對數(shù)方程時,要重視考慮對數(shù)的真數(shù)、底數(shù)的范圍;
解決對數(shù)不等式、對數(shù)方程時,要重視考慮對數(shù)的真數(shù)、底數(shù)的范圍;
 對數(shù)不等式的主要解決思想是對數(shù)函數(shù)的單調(diào)性。
對數(shù)不等式的主要解決思想是對數(shù)函數(shù)的單調(diào)性。
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com