
 對于線性相關(guān)系數(shù)敘述正確的是
對于線性相關(guān)系數(shù)敘述正確的是

 ,
, 越大,相關(guān)程度越大,反之,相關(guān)程度越小;
越大,相關(guān)程度越大,反之,相關(guān)程度越小;

 ,
, 越大,相關(guān)程度越大,反之,相關(guān)程度越小;
越大,相關(guān)程度越大,反之,相關(guān)程度越小;

 ≤
≤ ,且
,且 越接近
越接近 ,相關(guān)程度越大,
,相關(guān)程度越大, 越接近
越接近 ,相關(guān)程度越小;
,相關(guān)程度越小;
 以上說法均不對.
以上說法均不對.
 設(shè)有一個回歸方程
設(shè)有一個回歸方程 ,則變量
,則變量 增加一個單位時
增加一個單位時

 平均增加
平均增加 個單位;
個單位; 
 平均增加
平均增加 個單位;
個單位;

 平均減少
平均減少 個單位;
個單位; 
 平均減少
平均減少 個單位;
個單位;
 利用簡單隨機抽樣的方法,從
利用簡單隨機抽樣的方法,從 個個體(
個個體( )中抽取
)中抽取 個個體,依次抽取.
個個體,依次抽取.
若第二次抽取后,余下的每個個體被抽取的概率為 ,則在整個抽取過程中,每個個體被抽取的概率為
,則在整個抽取過程中,每個個體被抽取的概率為 







問題1. (
( 全國Ⅱ文)一個總體含有
全國Ⅱ文)一個總體含有 個個體,以簡單隨機抽樣方式從該總體中抽取一個容量為
個個體,以簡單隨機抽樣方式從該總體中抽取一個容量為 的樣本,則指定的某個個體被抽到的概率為
的樣本,則指定的某個個體被抽到的概率為
 (
( 浙江文)某校有學(xué)生
浙江文)某校有學(xué)生 人,其中高三學(xué)生
人,其中高三學(xué)生 人,為了解學(xué)生的身體素質(zhì)情況,彩用按年級分層抽樣的方法,從該校學(xué)生中抽取一個
人,為了解學(xué)生的身體素質(zhì)情況,彩用按年級分層抽樣的方法,從該校學(xué)生中抽取一個 人的樣本,則樣本中高三學(xué)生的人數(shù)為
人的樣本,則樣本中高三學(xué)生的人數(shù)為
 (
( 湖南)某公司甲、乙、丙、丁四個地區(qū)分別有
湖南)某公司甲、乙、丙、丁四個地區(qū)分別有 個、
個、 個、
個、 個、
個、 個銷售點.公司為了調(diào)查產(chǎn)品的情況,需從這
個銷售點.公司為了調(diào)查產(chǎn)品的情況,需從這 個銷售點中抽取一個容量為
個銷售點中抽取一個容量為 的樣本,記這項調(diào)查為①;在丙地區(qū)中有
的樣本,記這項調(diào)查為①;在丙地區(qū)中有 個特大型銷售點,要從中抽取
個特大型銷售點,要從中抽取 個調(diào)查其收入和售后服務(wù)等情況,記這項調(diào)查為②.則完成這兩項調(diào)查宜采用的抽樣方法依次為
個調(diào)查其收入和售后服務(wù)等情況,記這項調(diào)查為②.則完成這兩項調(diào)查宜采用的抽樣方法依次為
 分層抽樣法,系統(tǒng)抽樣法
分層抽樣法,系統(tǒng)抽樣法  分層抽樣法,簡單隨機抽樣法
分層抽樣法,簡單隨機抽樣法
 系統(tǒng)抽樣法,分層抽樣法
系統(tǒng)抽樣法,分層抽樣法  簡單隨機抽樣法,分層抽樣法
簡單隨機抽樣法,分層抽樣法
 (
( 屆高三湖北省六校)設(shè)下表是某班學(xué)生在一次數(shù)學(xué)考試中數(shù)學(xué)成績的分布表
屆高三湖北省六校)設(shè)下表是某班學(xué)生在一次數(shù)學(xué)考試中數(shù)學(xué)成績的分布表
|
分數(shù) |
 , , |
 , , |
 , , |
 , , |
 , , |
 , , |
 , , |
 , , |
|
人數(shù) |
 |
 |
 |
 |
 |
 |
 |
 |
那么分數(shù)在 中和分數(shù)不滿
中和分數(shù)不滿 分的頻率和累積頻率分別是
分的頻率和累積頻率分別是

 ,
,

 ,
,

 ,
,

 ,
,
 (
( 湖北文)為了了解某學(xué)校學(xué)生的身體發(fā)育情況,抽查了該校
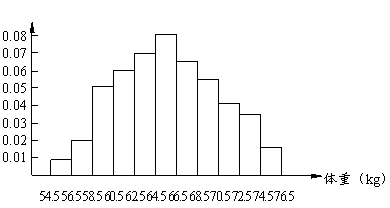
湖北文)為了了解某學(xué)校學(xué)生的身體發(fā)育情況,抽查了該校 名高中男生的體重情況,根據(jù)所得數(shù)據(jù)畫出樣本的頻率分布直方圖如右圖所示.根據(jù)此圖,估計該校
名高中男生的體重情況,根據(jù)所得數(shù)據(jù)畫出樣本的頻率分布直方圖如右圖所示.根據(jù)此圖,估計該校 名高中男生中體重大于
名高中男生中體重大于 公斤的人數(shù)為
公斤的人數(shù)為 








 (
( 湖南)設(shè)隨機變量
湖南)設(shè)隨機變量 服從標準正態(tài)分布
服從標準正態(tài)分布 ,已知
,已知 ,
,
則








 (
( 安徽)以
安徽)以 表示標準正態(tài)總體在區(qū)間
表示標準正態(tài)總體在區(qū)間 內(nèi)取值的概率,若隨機變量
內(nèi)取值的概率,若隨機變量 服從正態(tài)分布
服從正態(tài)分布 ,則概率
,則概率 等于
等于








問題2.已知從某批材料中任取一件時,取得的材料的強度 服從
服從 .
.
 計算取得的這件材料的強度不低于
計算取得的這件材料的強度不低于 的概率;
的概率; 如果所用的材料要求以
如果所用的材料要求以 的概率保證強度不低于
的概率保證強度不低于 ,問這些材料是否符合這個要求.
,問這些材料是否符合這個要求.
問題3.( 湖北)在生產(chǎn)過程中,測得纖維產(chǎn)品的纖度(表示纖維粗細的一種量)共有
湖北)在生產(chǎn)過程中,測得纖維產(chǎn)品的纖度(表示纖維粗細的一種量)共有 個數(shù)據(jù),將數(shù)據(jù)分組如右表:
個數(shù)據(jù),將數(shù)據(jù)分組如右表:
|
分組 |
頻數(shù) |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
合計 |
 |
 在答題卡上完成頻率分布表,并在給定的坐標系中畫出頻率分布直方圖;
在答題卡上完成頻率分布表,并在給定的坐標系中畫出頻率分布直方圖;
 估計纖度落在
估計纖度落在 中的概率及纖度小于
中的概率及纖度小于 的概率是多少?
的概率是多少?
 統(tǒng)計方法中,同一組數(shù)據(jù)常用該組區(qū)間的中點值(例如區(qū)間
統(tǒng)計方法中,同一組數(shù)據(jù)常用該組區(qū)間的中點值(例如區(qū)間 的中點值是
的中點值是 )作為代表.據(jù)此,估計纖度的期望.
)作為代表.據(jù)此,估計纖度的期望.












問題5.假設(shè)關(guān)于某設(shè)備的使用年限 和所支出的維修費用
和所支出的維修費用 (萬元),有如下的統(tǒng)計資料:
(萬元),有如下的統(tǒng)計資料:
若由資料可知 與
與 間呈線性相關(guān)關(guān)系.試求:
間呈線性相關(guān)關(guān)系.試求:
 線性回歸方程;
線性回歸方程; 估計使用年限為
估計使用年限為 年時,維修費用是多少?
年時,維修費用是多少?
 簡單隨機抽樣:設(shè)一個總體的個體數(shù)為
簡單隨機抽樣:設(shè)一個總體的個體數(shù)為 .如果通過逐個抽取的方法從中抽取一個樣本,且每次抽取時各個個體被抽到的概率相等,就稱這樣的抽樣為簡單隨機抽樣.
.如果通過逐個抽取的方法從中抽取一個樣本,且每次抽取時各個個體被抽到的概率相等,就稱這樣的抽樣為簡單隨機抽樣.
總結(jié):⑴一般地,用簡單隨機抽樣從含有 個個體的總體中抽取一個容量為
個個體的總體中抽取一個容量為 的樣本時,每次抽取一個個體時任一個體被抽到的概率為
的樣本時,每次抽取一個個體時任一個體被抽到的概率為 ;在整個抽樣過程中各個個體被抽到的概率為
;在整個抽樣過程中各個個體被抽到的概率為 ;
;
 簡單隨機抽樣的實施方法:
簡單隨機抽樣的實施方法:
⑴抽簽法:先將總體中的所有個體(共有 個)編號(號碼可從
個)編號(號碼可從 到
到 ),并把號碼寫在形狀、大小相同的號簽上(號簽可用小球、卡片、紙條等制作),然后將這些號簽放在同一個箱子里,進行均勻攪拌,抽簽時每次從中抽一個號簽,連續(xù)抽取
),并把號碼寫在形狀、大小相同的號簽上(號簽可用小球、卡片、紙條等制作),然后將這些號簽放在同一個箱子里,進行均勻攪拌,抽簽時每次從中抽一個號簽,連續(xù)抽取 次,就得到一個容量為
次,就得到一個容量為 的樣本
的樣本  適用范圍:總體的個體數(shù)不多時 優(yōu)點:抽簽法簡便易行,當(dāng)總體的個體數(shù)不太多時適宜采用抽簽法.
適用范圍:總體的個體數(shù)不多時 優(yōu)點:抽簽法簡便易行,當(dāng)總體的個體數(shù)不太多時適宜采用抽簽法.
⑵隨機數(shù)表法: 制定隨機數(shù)表;
制定隨機數(shù)表; 給總體中各個個體編號;
給總體中各個個體編號; 按照一定的規(guī)則確定所要抽取的樣本的號碼
按照一定的規(guī)則確定所要抽取的樣本的號碼
隨機數(shù)表抽樣“三步曲”:第一步,將總體中的個體編號;第二步,選定開始的數(shù)字;第三步,獲取樣本號碼
 簡單隨機抽樣的特點:它是不放回抽樣;它是逐個地進行抽取;它是一種等概率抽樣,簡單隨機抽樣方法,體現(xiàn)了抽樣的客觀性與公平性,是其他更復(fù)雜抽樣方法的基礎(chǔ).
簡單隨機抽樣的特點:它是不放回抽樣;它是逐個地進行抽取;它是一種等概率抽樣,簡單隨機抽樣方法,體現(xiàn)了抽樣的客觀性與公平性,是其他更復(fù)雜抽樣方法的基礎(chǔ).
 系統(tǒng)抽樣:當(dāng)總體中的個體數(shù)較多時,可將總體分成均衡的幾個部分,然后按預(yù)先定出的規(guī)則,從每一部分抽取一個個體,得到需要的樣本,這種抽樣叫做系統(tǒng)抽樣
系統(tǒng)抽樣:當(dāng)總體中的個體數(shù)較多時,可將總體分成均衡的幾個部分,然后按預(yù)先定出的規(guī)則,從每一部分抽取一個個體,得到需要的樣本,這種抽樣叫做系統(tǒng)抽樣
 系統(tǒng)抽樣的步驟:
系統(tǒng)抽樣的步驟:
①采用隨機的方式將總體中的個體編號 為簡便起見,有時可直接采用個體所帶有的號碼,如考生的準考證號、街道上各戶的門牌號,等等
為簡便起見,有時可直接采用個體所帶有的號碼,如考生的準考證號、街道上各戶的門牌號,等等
②即確定分段間隔:為將整個的編號分段(即分成幾個部分),要確定分段的間隔 當(dāng)
當(dāng) (
( 為總體中的個體的個數(shù),
為總體中的個體的個數(shù), 為樣本容量)是整數(shù)時,
為樣本容量)是整數(shù)時,
 ;當(dāng)
;當(dāng) 不是整數(shù)時,通過從總體中剔除一些個體使剩下的總體中個體的個數(shù)
不是整數(shù)時,通過從總體中剔除一些個體使剩下的總體中個體的個數(shù) 能被
能被 整除,這時
整除,這時
 .
.
③在第一段用簡單隨機抽樣確定起始的個體編號
④按照事先確定的規(guī)則抽取樣本(通常是將 加上間隔
加上間隔 ,得到第
,得到第 個編號
個編號 ,第
,第 個編號
個編號 ,這樣繼續(xù)下去,直到獲取整個樣本)
,這樣繼續(xù)下去,直到獲取整個樣本)
說明:①系統(tǒng)抽樣適用于總體中的個體數(shù)較多的情況,它與簡單隨機抽樣的聯(lián)系在于:將總體均分后的每一部分進行抽樣時,采用的是簡單隨機抽樣;
②與簡單隨機抽樣一樣,系統(tǒng)抽樣是等概率抽樣,它是客觀的、公平的.
③總體中的個體數(shù)恰好能被樣本容量整除時,可用它們的比值作為系統(tǒng)抽樣的間隔;當(dāng)總體中的個體數(shù)不能被樣本容量整除時,可用簡單隨機抽樣先從總體中剔除少量個體,使剩下的個體數(shù)能被樣本容量整除在進行系統(tǒng)抽樣
 分層抽樣: 當(dāng)已知總體由差異明顯的幾部分組成時,為了使樣本更充分地反映總體的情況,常將總體分成幾部分,然后按照各部分所占的比例進行抽樣,這種抽樣叫做分層抽樣,所分成的部分叫做層
分層抽樣: 當(dāng)已知總體由差異明顯的幾部分組成時,為了使樣本更充分地反映總體的情況,常將總體分成幾部分,然后按照各部分所占的比例進行抽樣,這種抽樣叫做分層抽樣,所分成的部分叫做層
 不放回抽樣和放回抽樣:在抽樣中,如果每次抽出個體后不再將它放回總體,稱這樣的抽樣為不放回抽樣;如果每次抽出個體后再將它放回總體,稱這樣的抽樣為放回抽樣.
不放回抽樣和放回抽樣:在抽樣中,如果每次抽出個體后不再將它放回總體,稱這樣的抽樣為不放回抽樣;如果每次抽出個體后再將它放回總體,稱這樣的抽樣為放回抽樣.
隨機抽樣、系統(tǒng)抽樣、分層抽樣都是不放回抽樣
常用的抽樣方法及它們之間的聯(lián)系和區(qū)別:
|
類別 |
共同點 |
各自特點 |
相互聯(lián)系 |
適用范圍 |
|
簡單隨機 抽樣 |
 抽樣過程中每個個體被抽取的概率是相同的; 抽樣過程中每個個體被抽取的概率是相同的; 都是不放回抽樣. 都是不放回抽樣. |
從總體中逐個抽取 |
|
總體中的個數(shù)比較少 |
|
系統(tǒng)抽樣 |
將總體均勻分成幾個部分,按照事先確定的規(guī)則在各部分抽取 |
在起始部分抽樣時采用簡單隨機抽樣 |
總體中的個數(shù)比較多 |
|
|
分層抽樣 |
將總體分成幾層,分層進行抽取 |
各層抽樣時采用簡單抽樣或者相同抽樣 |
總體由差異明顯的幾部分組成 |
 總體:在數(shù)理統(tǒng)計中,通常把被研究的對象的全體叫做總體.
總體:在數(shù)理統(tǒng)計中,通常把被研究的對象的全體叫做總體.
 頻率分布:用樣本估計總體,是研究統(tǒng)計問題的基本思想方法,樣本中所有數(shù)據(jù)(或數(shù)據(jù)組)的頻數(shù)和樣本容量的比,就是該數(shù)據(jù)的頻率.所有數(shù)據(jù)(或數(shù)據(jù)組)的頻率的分布變化規(guī)律叫做樣本的頻率分布.可以用樣本頻率表、樣本頻率分布條形圖或頻率分布直方圖來表示.
頻率分布:用樣本估計總體,是研究統(tǒng)計問題的基本思想方法,樣本中所有數(shù)據(jù)(或數(shù)據(jù)組)的頻數(shù)和樣本容量的比,就是該數(shù)據(jù)的頻率.所有數(shù)據(jù)(或數(shù)據(jù)組)的頻率的分布變化規(guī)律叫做樣本的頻率分布.可以用樣本頻率表、樣本頻率分布條形圖或頻率分布直方圖來表示.
 總體分布:從總體中抽取一個個體,就是一次隨機試驗,從總體中抽取一個容量為
總體分布:從總體中抽取一個個體,就是一次隨機試驗,從總體中抽取一個容量為 的樣本,就是進行了
的樣本,就是進行了 次試驗,試驗連同所出現(xiàn)的結(jié)果叫隨機事件,所有這些事件的概率分布規(guī)律稱為總體分布.
次試驗,試驗連同所出現(xiàn)的結(jié)果叫隨機事件,所有這些事件的概率分布規(guī)律稱為總體分布.

 總體密度曲線:樣本容量越大,所分組數(shù)越多,各組的頻率就越接近于總體在相應(yīng)各組取值的概率.設(shè)想樣本容量無限增大,分組的組距無限縮小,那么頻率分布直方圖就會無限接近于一條光滑曲線,這條曲線叫做總體密度曲線.
總體密度曲線:樣本容量越大,所分組數(shù)越多,各組的頻率就越接近于總體在相應(yīng)各組取值的概率.設(shè)想樣本容量無限增大,分組的組距無限縮小,那么頻率分布直方圖就會無限接近于一條光滑曲線,這條曲線叫做總體密度曲線.

 總體分布密度密度曲線函數(shù)
總體分布密度密度曲線函數(shù) 的兩條基本性質(zhì):
的兩條基本性質(zhì):
① ≥
≥ (
( );②由曲線
);②由曲線 與
與 軸圍成面積為
軸圍成面積為 .
.
 解決總體分布估計問題的一般程序如下:
解決總體分布估計問題的一般程序如下: 先確定分組的組數(shù)(最大數(shù)據(jù)與最小數(shù)據(jù)之差除以組距得組數(shù));
先確定分組的組數(shù)(最大數(shù)據(jù)與最小數(shù)據(jù)之差除以組距得組數(shù)); 分別計算各組的頻數(shù)及頻率(頻率
分別計算各組的頻數(shù)及頻率(頻率
 );
); 畫出頻率分布直方圖,并作出相應(yīng)的估計.
畫出頻率分布直方圖,并作出相應(yīng)的估計.
 條形圖是用其高度表示取各值的頻率;直方圖是用圖形面積的大小表示在各區(qū)間內(nèi)取值的頻率;累積頻率分布圖是一條折線,利用任意兩端值的累積頻率之差表示樣本數(shù)據(jù)在這兩點值之間的頻率.
條形圖是用其高度表示取各值的頻率;直方圖是用圖形面積的大小表示在各區(qū)間內(nèi)取值的頻率;累積頻率分布圖是一條折線,利用任意兩端值的累積頻率之差表示樣本數(shù)據(jù)在這兩點值之間的頻率.
 正態(tài)分布密度函數(shù):
正態(tài)分布密度函數(shù):
 ,(
,( )
)
其中 是圓周率;
是圓周率; 是自然對數(shù)的底;
是自然對數(shù)的底; 是隨機變量的取值;
是隨機變量的取值; 為正態(tài)分布的均值;
為正態(tài)分布的均值; 是正態(tài)分布的標準差.正態(tài)分布一般記為
是正態(tài)分布的標準差.正態(tài)分布一般記為 。
。
即若 ,則
,則 ,
,
 正態(tài)分布
正態(tài)分布 是由均值
是由均值 和標準差
和標準差 唯一決定的分布
唯一決定的分布
通過固定其中一個值,討論均值與標準差對于正態(tài)曲線的影響 ,亦見課本 圖
圖



 通過對三組正態(tài)曲線分析,得出正態(tài)曲線具有的基本特征是兩頭底、中間高、左右對稱.從形態(tài)上看,正態(tài)分布是一條單峰、對稱呈鐘形的曲線 .
通過對三組正態(tài)曲線分析,得出正態(tài)曲線具有的基本特征是兩頭底、中間高、左右對稱.從形態(tài)上看,正態(tài)分布是一條單峰、對稱呈鐘形的曲線 .
 正態(tài)曲線的性質(zhì):
正態(tài)曲線的性質(zhì):
 曲線在
曲線在 軸的上方,與
軸的上方,與 軸不相交
軸不相交 曲線關(guān)于直線
曲線關(guān)于直線 對稱
對稱
 當(dāng)
當(dāng) 時,曲線位于最高點
時,曲線位于最高點
 當(dāng)
當(dāng) 時,曲線上升(增函數(shù));當(dāng)
時,曲線上升(增函數(shù));當(dāng) 時,曲線下降(減函數(shù)).并且
時,曲線下降(減函數(shù)).并且
當(dāng)曲線向左、右兩邊無限延伸時,以 軸為漸近線,向它無限靠近
軸為漸近線,向它無限靠近

 一定時,曲線的形狀由
一定時,曲線的形狀由 確定
確定
 越大,曲線越“矮胖”,總體分布越分散;
越大,曲線越“矮胖”,總體分布越分散; 越小.曲線越“瘦高”.總體分布越集中
越小.曲線越“瘦高”.總體分布越集中
 正態(tài)曲線下的總面積等于
正態(tài)曲線下的總面積等于 .即
.即
 標準正態(tài)曲線:當(dāng)
標準正態(tài)曲線:當(dāng) 、
、 時,正態(tài)總體稱為標準正態(tài)總體,其相應(yīng)的函數(shù)表示式是
時,正態(tài)總體稱為標準正態(tài)總體,其相應(yīng)的函數(shù)表示式是 ,(
,( ),其相應(yīng)的曲線稱為標準正態(tài)曲線
),其相應(yīng)的曲線稱為標準正態(tài)曲線
標準正態(tài)總體 在正態(tài)總體的研究中占有重要的地位
在正態(tài)總體的研究中占有重要的地位
 任何正態(tài)分布的概率問題均可轉(zhuǎn)化成標準正態(tài)分布的概率問題
任何正態(tài)分布的概率問題均可轉(zhuǎn)化成標準正態(tài)分布的概率問題
 標準正態(tài)分布表及標準正態(tài)總體在任一區(qū)間
標準正態(tài)分布表及標準正態(tài)總體在任一區(qū)間 的概率問題:
的概率問題:
 標準正態(tài)總體
標準正態(tài)總體 在正態(tài)總體的研究中有非常重要的地位,為此專門制作了“標準正態(tài)分布表”.在這個表中,對應(yīng)于
在正態(tài)總體的研究中有非常重要的地位,為此專門制作了“標準正態(tài)分布表”.在這個表中,對應(yīng)于 的值
的值 是指總體取值小于
是指總體取值小于 的概率,即
的概率,即  ,
, .
.
對于標準正態(tài)總體 ,
, 是總體取值小于
是總體取值小于 的概率,即
的概率,即
其中 ,圖中陰影部分的面積表示為概率
,圖中陰影部分的面積表示為概率
 只要有標準正態(tài)分布表即可查表解決.從圖中不難發(fā)現(xiàn):當(dāng)
只要有標準正態(tài)分布表即可查表解決.從圖中不難發(fā)現(xiàn):當(dāng) 時,
時, ;而當(dāng)
;而當(dāng) 時,
時, ,利用標準正態(tài)分布表,可以求出標準正態(tài)總體在任意區(qū)間
,利用標準正態(tài)分布表,可以求出標準正態(tài)總體在任意區(qū)間 內(nèi)取值的概率,即直線
內(nèi)取值的概率,即直線 ,
, 與正態(tài)曲線、
與正態(tài)曲線、 軸所圍成的曲邊梯形的面積
軸所圍成的曲邊梯形的面積
故:
 ;
;
 ;
;
 若
若 ,則
,則
任一的正態(tài)總體 均可化成標準正態(tài)總體
均可化成標準正態(tài)總體 來進行研究,
來進行研究,
對任一的正態(tài)總體 來說,取值小于
來說,取值小于 的概率
的概率
對于正態(tài)總體 取值的概率:
取值的概率:



在區(qū)間 、
、 、
、 內(nèi)取值的概率分別為
內(nèi)取值的概率分別為 、
、 、
、
 因此我們時常只在區(qū)間
因此我們時常只在區(qū)間 內(nèi)研究正態(tài)總體分布情況,而忽略其中很小的一部分
內(nèi)研究正態(tài)總體分布情況,而忽略其中很小的一部分 
 小概率事件的含義
小概率事件的含義
發(fā)生概率一般不超過 的事件,即事件在一次試驗中幾乎不可能發(fā)生
的事件,即事件在一次試驗中幾乎不可能發(fā)生
假設(shè)檢驗方法的基本思想:首先,假設(shè)總體應(yīng)是或近似為正態(tài)總體,然后,依照小概率事件幾乎不可能在一次試驗中發(fā)生的原理對試驗結(jié)果進行分析
假設(shè)檢驗方法的操作程序,即“三步曲”
 提出統(tǒng)計假設(shè),具體問題里的統(tǒng)計假設(shè)服從正態(tài)分布
提出統(tǒng)計假設(shè),具體問題里的統(tǒng)計假設(shè)服從正態(tài)分布
 是確定一次試驗中的
是確定一次試驗中的 值是否落入范圍
值是否落入范圍 ;
;
 是作出推斷:若
是作出推斷:若
 ,接受統(tǒng)計假設(shè);若
,接受統(tǒng)計假設(shè);若
 ,由于這是小概率事件,就拒絕統(tǒng)計假設(shè),說明生產(chǎn)過程中出現(xiàn)了異常情況
,由于這是小概率事件,就拒絕統(tǒng)計假設(shè),說明生產(chǎn)過程中出現(xiàn)了異常情況
 相關(guān)關(guān)系的概念
相關(guān)關(guān)系的概念
當(dāng)自變量一定時,因變量的取值帶有一定的隨機性的兩個變量之間的關(guān)系稱為相關(guān)關(guān)系
相關(guān)關(guān)系是非隨機變量與隨機變量之間的關(guān)系,函數(shù)關(guān)系是兩個非隨機變量之間的關(guān)系,是一種因果關(guān)系,而相關(guān)關(guān)系不一定是因果關(guān)系,所以相關(guān)關(guān)系與函數(shù)關(guān)系不同,其變量具有隨機性,因此相關(guān)關(guān)系是一種非確定性關(guān)系  (有因果關(guān)系,也有伴隨關(guān)系).因此,相關(guān)關(guān)系與函數(shù)關(guān)系的異同點如下:
(有因果關(guān)系,也有伴隨關(guān)系).因此,相關(guān)關(guān)系與函數(shù)關(guān)系的異同點如下:
相同點:均是指兩個變量的關(guān)系.
不同點:函數(shù)關(guān)系是一種確定的關(guān)系;而相關(guān)關(guān)系是一種非確定關(guān)系;函數(shù)關(guān)系是自變量與因變量之間的關(guān)系,這種關(guān)系是兩個非隨機變量的關(guān)系;而相關(guān)關(guān)系是非隨機變量與隨機變量的關(guān)系.
 回歸分析: 對具有相關(guān)關(guān)系的兩個變量進行統(tǒng)計分析的方法叫做回歸分析
回歸分析: 對具有相關(guān)關(guān)系的兩個變量進行統(tǒng)計分析的方法叫做回歸分析 通俗地講,回歸分析是尋找相關(guān)關(guān)系中非確定性關(guān)系的某種確定性.
通俗地講,回歸分析是尋找相關(guān)關(guān)系中非確定性關(guān)系的某種確定性.
 散點圖:表示具有相關(guān)關(guān)系的兩個變量的一組數(shù)據(jù)的圖形叫做散點圖.散點圖形象地反映了各對數(shù)據(jù)的密切程度
散點圖:表示具有相關(guān)關(guān)系的兩個變量的一組數(shù)據(jù)的圖形叫做散點圖.散點圖形象地反映了各對數(shù)據(jù)的密切程度  粗略地看,散點分布具有一定的規(guī)律.
粗略地看,散點分布具有一定的規(guī)律.
 回歸直線
回歸直線
設(shè)所求的直線方程為 ,其中
,其中 、
、 是待定系數(shù).
是待定系數(shù).
則 .于是得到各個偏差
.于是得到各個偏差
 .
.
顯見,偏差 的符號有正有負,若將它們相加會造成相互抵消,所以它們的和不能代表幾個點與相應(yīng)直線在整體上的接近程度,故采用
的符號有正有負,若將它們相加會造成相互抵消,所以它們的和不能代表幾個點與相應(yīng)直線在整體上的接近程度,故采用 個偏差的平方和.
個偏差的平方和.

表示 個點與相應(yīng)直線在整體上的接近程度.
個點與相應(yīng)直線在整體上的接近程度.
記  (說明
(說明 的意義).
的意義).
上述式子展開后,是一個關(guān)于 、
、 的二次多項式,應(yīng)用配方法,可求出使
的二次多項式,應(yīng)用配方法,可求出使 為最小值時的
為最小值時的 、
、 的值.即
的值.即
 ,
,  ,
,
相應(yīng)的直線叫做回歸直線,對兩個變量所進行的上述統(tǒng)計分析叫做回歸分析.
特別指出:
 對回歸直線方程只要求會運用它進行具體計算
對回歸直線方程只要求會運用它進行具體計算 、
、 ,求出回歸直線方程即可.不要求掌握回歸直線方程的推導(dǎo)過程.
,求出回歸直線方程即可.不要求掌握回歸直線方程的推導(dǎo)過程.
 求回歸直線方程,首先應(yīng)注意到,只有在散點圖大致呈線性時,求出的回歸直線方程才有實標意義.否則,求出的回歸直線方程毫無意義.因此,對一組數(shù)據(jù)作線性回歸分析時,應(yīng)先看其散點圖是否成線性.
求回歸直線方程,首先應(yīng)注意到,只有在散點圖大致呈線性時,求出的回歸直線方程才有實標意義.否則,求出的回歸直線方程毫無意義.因此,對一組數(shù)據(jù)作線性回歸分析時,應(yīng)先看其散點圖是否成線性.
 求回歸直線方程,關(guān)鍵在于正確地求出系數(shù)
求回歸直線方程,關(guān)鍵在于正確地求出系數(shù) 、
、 ,由于求
,由于求 、
、 的計算量較大,計算時仔細謹慎、分層進行,避免因計算產(chǎn)生失誤.
的計算量較大,計算時仔細謹慎、分層進行,避免因計算產(chǎn)生失誤.
 回歸直線方程在現(xiàn)實生活與生產(chǎn)中有廣泛的應(yīng)用.應(yīng)用回歸直線方程可以把非確定性問題轉(zhuǎn)化成確定性問題,把“無序”變?yōu)椤坝行颉保η闆r進行估測、補充.因此,學(xué)過回歸直線方程以后,應(yīng)增強學(xué)生應(yīng)用回歸直線方程解決相關(guān)實際問題的意識.
回歸直線方程在現(xiàn)實生活與生產(chǎn)中有廣泛的應(yīng)用.應(yīng)用回歸直線方程可以把非確定性問題轉(zhuǎn)化成確定性問題,把“無序”變?yōu)椤坝行颉保η闆r進行估測、補充.因此,學(xué)過回歸直線方程以后,應(yīng)增強學(xué)生應(yīng)用回歸直線方程解決相關(guān)實際問題的意識.
 相關(guān)系數(shù):相關(guān)系數(shù)是因果統(tǒng)計學(xué)家皮爾遜提出的,對于變量
相關(guān)系數(shù):相關(guān)系數(shù)是因果統(tǒng)計學(xué)家皮爾遜提出的,對于變量 與
與 的一組觀測值,把
的一組觀測值,把
 =
=
叫做變量 與
與 之間的樣本相關(guān)系數(shù),簡稱相關(guān)系數(shù),用它來衡量兩個變量之間的線性相關(guān)程度.
之間的樣本相關(guān)系數(shù),簡稱相關(guān)系數(shù),用它來衡量兩個變量之間的線性相關(guān)程度.
 相關(guān)系數(shù)的性質(zhì):
相關(guān)系數(shù)的性質(zhì):  ≤
≤ ,且
,且 越接近
越接近 ,相關(guān)程度越大;且
,相關(guān)程度越大;且 越接近
越接近 ,相關(guān)程度越小.
,相關(guān)程度越小.
 顯著性水平:顯著性水平是統(tǒng)計假設(shè)檢驗中的一個概念,它是公認的小概率事件的概率值
顯著性水平:顯著性水平是統(tǒng)計假設(shè)檢驗中的一個概念,它是公認的小概率事件的概率值
 它必須在每一次統(tǒng)計檢驗之前確定
它必須在每一次統(tǒng)計檢驗之前確定
 顯著性檢驗:(相關(guān)系數(shù)檢驗的步驟):由顯著性水平和自由度查表得出臨界值,顯著性水平一般取
顯著性檢驗:(相關(guān)系數(shù)檢驗的步驟):由顯著性水平和自由度查表得出臨界值,顯著性水平一般取 和
和 ,自由度為
,自由度為 ,其中
,其中 是數(shù)據(jù)的個數(shù)
是數(shù)據(jù)的個數(shù)  在“相關(guān)系數(shù)檢驗的臨界值表”查出與顯著性水平
在“相關(guān)系數(shù)檢驗的臨界值表”查出與顯著性水平 或
或 及自由度
及自由度 (
( 為觀測值組數(shù))相應(yīng)的相關(guān)數(shù)臨界值
為觀測值組數(shù))相應(yīng)的相關(guān)數(shù)臨界值 或
或 ;例如
;例如 時,
時, ,
,
 求得的相關(guān)系數(shù)
求得的相關(guān)系數(shù) 和臨界值
和臨界值 比較,若
比較,若
 ,上面
,上面 與
與 是線性相關(guān)的,當(dāng)
是線性相關(guān)的,當(dāng) 或
或 ,認為線性關(guān)系不顯著
,認為線性關(guān)系不顯著
結(jié)論:討論若干變量是否線性相關(guān),必須先進行相關(guān)性檢驗,在確認線性相關(guān)后,再求回歸直線;
通過兩個變量是否線性相關(guān)的估計,實際上就是把非確定性問題轉(zhuǎn)化成確定性問題來研究;
 (
( 福建)一個均勻小正方體的
福建)一個均勻小正方體的 個面中,三個面上標以數(shù)
個面中,三個面上標以數(shù) ,兩個面上標以數(shù)
,兩個面上標以數(shù) ,一
,一
個面上標以數(shù) .將這個小正方體拋擲
.將這個小正方體拋擲 次,則向上的數(shù)之積的數(shù)學(xué)期望是
次,則向上的數(shù)之積的數(shù)學(xué)期望是
 (
( 四川文)某商場買來一車蘋果,從中隨機抽取了
四川文)某商場買來一車蘋果,從中隨機抽取了 個蘋果,其重量(單位:克)
個蘋果,其重量(單位:克)
分別為: ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,由此估計這車蘋果單個重量的期望值是
,由此估計這車蘋果單個重量的期望值是

 克
克 
 克
克 
 克
克 
 克
克
 (
( 湖南)某地區(qū)為下崗人員免費提供財會和計算機培訓(xùn),以提高下崗人員的再就業(yè)能力,每名下崗人員可以選擇參加一項培訓(xùn)、參加兩項培訓(xùn)或不參加培訓(xùn),已知參加過財會培訓(xùn)的有
湖南)某地區(qū)為下崗人員免費提供財會和計算機培訓(xùn),以提高下崗人員的再就業(yè)能力,每名下崗人員可以選擇參加一項培訓(xùn)、參加兩項培訓(xùn)或不參加培訓(xùn),已知參加過財會培訓(xùn)的有 ,參加過計算機培訓(xùn)的有
,參加過計算機培訓(xùn)的有 ,假設(shè)每個人對培訓(xùn)項目的選擇是相互獨立的,且各人的選擇相互之間沒有影響.
,假設(shè)每個人對培訓(xùn)項目的選擇是相互獨立的,且各人的選擇相互之間沒有影響.
 任選
任選 名下崗人員,求該人參加過培訓(xùn)的概率;
名下崗人員,求該人參加過培訓(xùn)的概率;
 任選
任選 名下崗人員,記
名下崗人員,記 為
為 人中參加過培訓(xùn)的人數(shù),求
人中參加過培訓(xùn)的人數(shù),求 的分布列和期望.
的分布列和期望.
 (
( 四川)廠家在產(chǎn)品出廠前,需對產(chǎn)品做檢驗,廠家將一批產(chǎn)品發(fā)給商家時,商家按合同規(guī)定也需隨機抽取一定數(shù)量的產(chǎn)品做檢驗,以決定是否接收這批產(chǎn)品.
四川)廠家在產(chǎn)品出廠前,需對產(chǎn)品做檢驗,廠家將一批產(chǎn)品發(fā)給商家時,商家按合同規(guī)定也需隨機抽取一定數(shù)量的產(chǎn)品做檢驗,以決定是否接收這批產(chǎn)品.
 若廠家?guī)旆恐械拿考a(chǎn)品合格的概率為
若廠家?guī)旆恐械拿考a(chǎn)品合格的概率為 ,從中任意取出
,從中任意取出 件進行檢驗.求至少有
件進行檢驗.求至少有 件是合格品的概率;
件是合格品的概率;
 若廠家發(fā)給商家
若廠家發(fā)給商家 件產(chǎn)品,其中有
件產(chǎn)品,其中有 件不合格,按合同規(guī)定該商家從中任取
件不合格,按合同規(guī)定該商家從中任取 件,都進行檢驗,只有
件,都進行檢驗,只有 件都合格時才接收這批產(chǎn)品,否則拒收.求該商家可能檢驗出不合格產(chǎn)品數(shù)
件都合格時才接收這批產(chǎn)品,否則拒收.求該商家可能檢驗出不合格產(chǎn)品數(shù) 的分布列及期望
的分布列及期望 ,并求該商家拒收這批產(chǎn)品的概率.
,并求該商家拒收這批產(chǎn)品的概率.








 已知
已知 的分布列為如右表:
的分布列為如右表:
則 ,
,
 拋擲一顆骰子,設(shè)所得點數(shù)為
拋擲一顆骰子,設(shè)所得點數(shù)為 ,則
,則 ,
,
 設(shè)服從二項分布
設(shè)服從二項分布 的隨機變量
的隨機變量 的期望和方差分別為
的期望和方差分別為 和
和 ,則二項分布的參數(shù)
,則二項分布的參數(shù) 的值為
的值為 
 ,
,

 ,
,

 ,
,

 ,
,








問題1. (
( 浙江)隨機變量
浙江)隨機變量 的分布列如右:
的分布列如右:
其中 成等差數(shù)列,若
成等差數(shù)列,若 ,則
,則 的值是
的值是
 設(shè)
設(shè) 是一個離散型隨機變量,其分布列如下表, 則
是一個離散型隨機變量,其分布列如下表, 則 ,則
,則
















 (
( 重慶聯(lián)考) 隨機變量
重慶聯(lián)考) 隨機變量 的分布列如右:
的分布列如右:
那么 等于
等于








 (
( 黃崗調(diào)研)已知
黃崗調(diào)研)已知 ,
, ,
, ,則
,則 與
與 的值分別為
的值分別為

 和
和

 和
和

 和
和

 和
和
 (
( 天津十校聯(lián)考)某一離散型隨機變量
天津十校聯(lián)考)某一離散型隨機變量 的概率分布如下表,且
的概率分布如下表,且 ,
,
則 的值為:
的值為:

















 (
( 四川) 設(shè)離散型隨機變量
四川) 設(shè)離散型隨機變量 可能取的值為
可能取的值為 ,
, (
( ),又
),又 的數(shù)學(xué)期望
的數(shù)學(xué)期望 ,則
,則
 |
 |
 |
 |
… |
 |
 |
 |
 |
 |
… |
 |
問題2.設(shè)隨機變量 的分布列如右表,求
的分布列如右表,求 和
和 .
.
問題3.有甲、乙兩種建筑材料,從中各取等量的樣品檢驗它們的抗拉強度指數(shù)如下:
























其中 和
和 分別表示甲、乙兩種材料的抗拉強度,在使用時要求抗拉強度不低于
分別表示甲、乙兩種材料的抗拉強度,在使用時要求抗拉強度不低于 的條件下,比較甲、乙兩種材料哪一種穩(wěn)定性好.
的條件下,比較甲、乙兩種材料哪一種穩(wěn)定性好.
問題4.( 全國Ⅱ)某批產(chǎn)品成箱包裝,每箱
全國Ⅱ)某批產(chǎn)品成箱包裝,每箱 件.一用戶在購進該批產(chǎn)品前先取出
件.一用戶在購進該批產(chǎn)品前先取出 箱,再從每箱中任意抽取
箱,再從每箱中任意抽取 件產(chǎn)品進行檢驗.設(shè)取出的第一、二、三箱中分別有
件產(chǎn)品進行檢驗.設(shè)取出的第一、二、三箱中分別有 件、
件、 件、
件、 件二等品,其余為一等品.
件二等品,其余為一等品. 用
用 表示抽檢的
表示抽檢的 件產(chǎn)品中二等品的件數(shù),求
件產(chǎn)品中二等品的件數(shù),求 的分布列及
的分布列及 的數(shù)學(xué)期望;
的數(shù)學(xué)期望; 若抽檢的
若抽檢的 件產(chǎn)品中有
件產(chǎn)品中有 件或
件或 件以上二等品,用戶就拒絕購買這批產(chǎn)品,求這批產(chǎn)品級用戶拒絕的概率.
件以上二等品,用戶就拒絕購買這批產(chǎn)品,求這批產(chǎn)品級用戶拒絕的概率.
問題5.( 遼寧)某企業(yè)準備投產(chǎn)一批特殊型號的產(chǎn)品,已知該種產(chǎn)品的成本
遼寧)某企業(yè)準備投產(chǎn)一批特殊型號的產(chǎn)品,已知該種產(chǎn)品的成本 與產(chǎn)量
與產(chǎn)量 的函數(shù)關(guān)系式為:
的函數(shù)關(guān)系式為:
該種產(chǎn)品的市場前景無法確定,有三種可能出現(xiàn)的情況,各種情形發(fā)生的概率及產(chǎn)品價格 與產(chǎn)量
與產(chǎn)量 的函數(shù)關(guān)系式如下表所示:
的函數(shù)關(guān)系式如下表所示:
|
市場情形 |
概率 |
價格 與產(chǎn)量 與產(chǎn)量 的函數(shù)關(guān)系式 的函數(shù)關(guān)系式 |
|
好 |
 |
 |
|
中 |
 |
 |
|
差 |
 |
 |
設(shè) 分別表示市場情形好、中差時的利潤,隨機變量
分別表示市場情形好、中差時的利潤,隨機變量 ,表示當(dāng)產(chǎn)量為
,表示當(dāng)產(chǎn)量為 ,而市場前景無法確定的利潤.
,而市場前景無法確定的利潤. 分別求利潤
分別求利潤 與產(chǎn)量
與產(chǎn)量 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
 當(dāng)產(chǎn)量
當(dāng)產(chǎn)量 確定時,求期望
確定時,求期望 ;
; 試問產(chǎn)量
試問產(chǎn)量 取何值時,
取何值時, 取得最大值.
取得最大值.
 數(shù)學(xué)期望: 一般地,若離散型隨機變量ξ的概率分布為
數(shù)學(xué)期望: 一般地,若離散型隨機變量ξ的概率分布為
 |
x1 |
x2 |
… |
xn |
… |
|
P |
p1 |
p2 |
… |
pn |
… |
則稱 

 …
… … 為ξ的數(shù)學(xué)期望,簡稱期望
… 為ξ的數(shù)學(xué)期望,簡稱期望
 數(shù)學(xué)期望是離散型隨機變量的一個特征數(shù),它反映了離散型隨機變量取值的平均水平
數(shù)學(xué)期望是離散型隨機變量的一個特征數(shù),它反映了離散型隨機變量取值的平均水平
 平均數(shù)、均值:一般地,在有限取值離散型隨機變量ξ的概率分布中,令
平均數(shù)、均值:一般地,在有限取值離散型隨機變量ξ的概率分布中,令
 …
… ,則有
,則有
 …
… ,
,

 …
… ,所以
,所以 的數(shù)學(xué)期望又稱為平均數(shù)、均值 .
的數(shù)學(xué)期望又稱為平均數(shù)、均值 .
 期望的一個性質(zhì):若
期望的一個性質(zhì):若 ,則
,則
 方差: 對于離散型隨機變量
方差: 對于離散型隨機變量 ,如果它所有可能取的值是
,如果它所有可能取的值是 ,
, ,…,
,…, ,…,
,…,
且取這些值的概率分別是 ,
, ,…,
,…, ,…,那么,
,…,那么,
 =
= +
+ +…+
+…+ +…
+…
稱為隨機變量 的均方差,簡稱為方差,式中的
的均方差,簡稱為方差,式中的 是隨機變量
是隨機變量 的期望.
的期望.
 標準差:
標準差: 的算術(shù)平方根
的算術(shù)平方根 叫做隨機變量ξ的標準差,記作
叫做隨機變量ξ的標準差,記作
 方差的性質(zhì):
方差的性質(zhì):
 ;
;
 .
.
 方差的意義:
方差的意義: 隨機變量
隨機變量 的方差的定義與一組數(shù)據(jù)的方差的定義式是相同的;
的方差的定義與一組數(shù)據(jù)的方差的定義式是相同的;
 隨機變量
隨機變量 的方差、標準差也是隨機變量
的方差、標準差也是隨機變量 的特征數(shù),它們都反映了隨機變量取值的穩(wěn)定與波動、集中與離散的程度;
的特征數(shù),它們都反映了隨機變量取值的穩(wěn)定與波動、集中與離散的程度; 標準差與隨機變量本身有相同的單位,所以在實際問題中應(yīng)用更廣泛.
標準差與隨機變量本身有相同的單位,所以在實際問題中應(yīng)用更廣泛.
 二項分布的期望與方差:若
二項分布的期望與方差:若 ,則
,則 ,
,
 幾何分布的期望和方差:
幾何分布的期望和方差:
若
 ,其中
,其中 ,…,
,…,  .則
.則 ,
, .
.
 (
( 重慶) 某大夏的一部電梯從底層出發(fā)后只能在第
重慶) 某大夏的一部電梯從底層出發(fā)后只能在第 、
、 、
、 層可以停靠。若該電梯在底層載有
層可以停靠。若該電梯在底層載有 位乘客,且每位乘客在這三層的每一層下電梯的概率均為
位乘客,且每位乘客在這三層的每一層下電梯的概率均為 ,用
,用 表示這
表示這 位乘客在第
位乘客在第 層下電梯的人數(shù),求:
層下電梯的人數(shù),求: 隨機變量
隨機變量 的分布列;
的分布列; 略.
略.
 (
( 江西)某商場舉行抽獎促銷活動,抽獎規(guī)則是:從裝有
江西)某商場舉行抽獎促銷活動,抽獎規(guī)則是:從裝有 個白球,
個白球, 個紅球的箱子中每次隨機地摸出一個球,記下顏色后放回,摸出一個紅球可獲得獎金
個紅球的箱子中每次隨機地摸出一個球,記下顏色后放回,摸出一個紅球可獲得獎金 元;摸出
元;摸出 個紅球可獲得獎金
個紅球可獲得獎金 元,現(xiàn)有甲,乙兩位顧客,規(guī)定:甲摸一次,乙摸兩次,令
元,現(xiàn)有甲,乙兩位顧客,規(guī)定:甲摸一次,乙摸兩次,令 表示甲,乙摸球后獲得的獎金總額。求:
表示甲,乙摸球后獲得的獎金總額。求:
 的分布列
的分布列  略.
略.
 設(shè)離散型隨機變量
設(shè)離散型隨機變量 的分布列
的分布列 ,
, .
.
 求常數(shù)
求常數(shù) 的值;
的值; 求
求 ;
; 求
求
 一袋中裝有
一袋中裝有 只球,編號為
只球,編號為 ,在袋中同時取
,在袋中同時取 只,以
只,以 表示取出的三只球中的最小號碼,寫出隨機變量
表示取出的三只球中的最小號碼,寫出隨機變量 的分布列
的分布列
 某人參加射擊,擊中目標的概率是
某人參加射擊,擊中目標的概率是 .
.
 設(shè)
設(shè) 為他射擊
為他射擊 次擊中目標的次數(shù),求隨機變量
次擊中目標的次數(shù),求隨機變量 的分布列;
的分布列;
 設(shè)
設(shè) 為他第一次擊中目標時所需要射擊的次數(shù),求
為他第一次擊中目標時所需要射擊的次數(shù),求 的分布列;
的分布列;
 若他只有
若他只有 顆子彈,若他擊中目標,則不再射擊,否則子彈打完,求他
顆子彈,若他擊中目標,則不再射擊,否則子彈打完,求他
射擊次數(shù) 的分布列.
的分布列.
問題1.( 陜西)甲、乙、丙
陜西)甲、乙、丙 人投籃,投進的概率分別是
人投籃,投進的概率分別是 、
、 、
、 .
.
 略.
略. 用
用 表示乙投籃
表示乙投籃 次的進球數(shù),求隨機變量
次的進球數(shù),求隨機變量 的概率分布及數(shù)學(xué)期望
的概率分布及數(shù)學(xué)期望
問題2.( 浙江)袋子
浙江)袋子 和
和 中裝有若干個均勻的紅球和白球,從
中裝有若干個均勻的紅球和白球,從 中摸出一個紅球的概率是
中摸出一個紅球的概率是 ,從
,從 中摸出一個紅球的概率為
中摸出一個紅球的概率為 . (Ⅰ) 從
. (Ⅰ) 從 中有放回地摸球,每次摸出一個,有
中有放回地摸球,每次摸出一個,有 次摸到紅球即停止.(ⅰ)求恰好摸
次摸到紅球即停止.(ⅰ)求恰好摸 次停止的概率;(ⅱ)記
次停止的概率;(ⅱ)記 次之內(nèi)(含
次之內(nèi)(含 次)摸到紅球的次數(shù)為
次)摸到紅球的次數(shù)為 ,求隨機變量
,求隨機變量 的分布率及數(shù)學(xué)期望
的分布率及數(shù)學(xué)期望 .(Ⅱ)略.
.(Ⅱ)略.
問題3.某射手進行射擊練習(xí),每射擊 發(fā)子彈算一組,一旦命中就停止射擊,并進行下一組練習(xí),否則一直打完
發(fā)子彈算一組,一旦命中就停止射擊,并進行下一組練習(xí),否則一直打完 發(fā)子彈后才能進行下一組練習(xí).若該射手的射擊命中率為
發(fā)子彈后才能進行下一組練習(xí).若該射手的射擊命中率為 ,求它在一組練習(xí)中所用子彈數(shù)目
,求它在一組練習(xí)中所用子彈數(shù)目 的分布列
的分布列
問題4.從一批有 個合格品與
個合格品與 個次品的產(chǎn)品中,一件一件地抽取產(chǎn)品,設(shè)各個產(chǎn)品被抽到的可能性相同.在下列三種情況下,分別求出直到取出合格品為止時所需抽取次數(shù)
個次品的產(chǎn)品中,一件一件地抽取產(chǎn)品,設(shè)各個產(chǎn)品被抽到的可能性相同.在下列三種情況下,分別求出直到取出合格品為止時所需抽取次數(shù) 的分布列:
的分布列: 每次抽出的產(chǎn)品都不放回此批產(chǎn)品中;
每次抽出的產(chǎn)品都不放回此批產(chǎn)品中; 每次抽出的產(chǎn)品都立即放回此批產(chǎn)品中,然后再取出一件產(chǎn)品;
每次抽出的產(chǎn)品都立即放回此批產(chǎn)品中,然后再取出一件產(chǎn)品; 每次取出一件產(chǎn)品后總把一件合格品放回此批產(chǎn)品中.
每次取出一件產(chǎn)品后總把一件合格品放回此批產(chǎn)品中.
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com