
問題1.
已知集合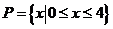 ,
, ,下列不表示從
,下列不表示從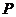 到
到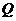 的映射是
的映射是

 :
:

 ∶
∶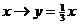

 ∶
∶

 ∶
∶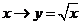
問題2.(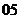 黃崗模擬)下列從
黃崗模擬)下列從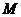 到
到 的各對應法則
的各對應法則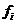 (
(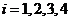 )中哪些是映射?哪些是函數(shù)?哪些不是映射?為什么?
)中哪些是映射?哪些是函數(shù)?哪些不是映射?為什么?
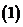
 直線
直線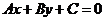
 ,
,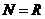 ,
, :求直線
:求直線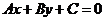 的斜率;
的斜率;
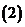
 直線
直線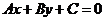
 ,
, ,
,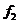 :求直線
:求直線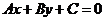 的傾斜角;
的傾斜角;
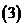 當
當 ,
,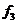 :求
:求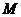 中每個元素的正切;
中每個元素的正切;
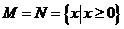 ,
,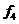 :求
:求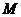 中每個元素的算術平方根.
中每個元素的算術平方根.
 平面
平面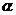 內(nèi)的矩形
內(nèi)的矩形 ,
,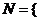 平面
平面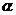 內(nèi)的圓
內(nèi)的圓 ,
, :作矩形的外接圓(此小題為編者自擬)
:作矩形的外接圓(此小題為編者自擬)
問題3. 已知
已知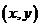 在映射
在映射 作用下的象是
作用下的象是 .①求
.①求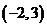 在
在 作用下的象②若在
作用下的象②若在 作用下的象是
作用下的象是 ,求它的原象
,求它的原象
 設集合
設集合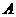 和
和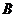 都是實數(shù)集,映射
都是實數(shù)集,映射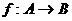 把集合
把集合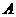 中的元素
中的元素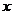 映射到集合
映射到集合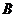 中的元素
中的元素 ,則在映射
,則在映射 下,象
下,象 的原象組成的集合是
的原象組成的集合是

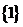



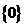


問題4.下列各對函數(shù)中,相同的是

 ,
,

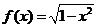 ,
,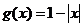 ,
,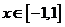

 ,
, ,
,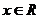

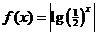 ,
,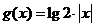
問題5.①(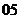 浙江文)設
浙江文)設 ,則
,則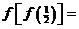





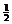


②(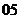 山東)函數(shù)
山東)函數(shù)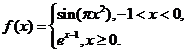 ,若
,若 ,
,
則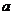 的所有可能值為
的所有可能值為


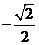

 ,
,

 ,
,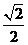
問題6.矩形 的長
的長 ,寬
,寬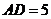 ,動點
,動點 、
、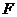 分別在
分別在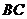 、
、 上,且
上,且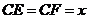 ,
,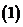 將
將 的面積
的面積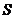 表示為
表示為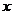 的函數(shù)
的函數(shù)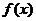 ,求函數(shù)
,求函數(shù)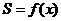 的解析式;
的解析式;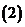 求
求 的最大值.
的最大值.
 對映射有兩個關鍵點:一是有象,二是象惟一,缺一不可;
對映射有兩個關鍵點:一是有象,二是象惟一,缺一不可;
 對函數(shù)三要素及其之間的關系給以深刻理解,這是處理函數(shù)問題的關鍵;
對函數(shù)三要素及其之間的關系給以深刻理解,這是處理函數(shù)問題的關鍵;
 理解函數(shù)和映射的關系,函數(shù)式和方程式的關系.
理解函數(shù)和映射的關系,函數(shù)式和方程式的關系.
 映射與函數(shù)的概念;
映射與函數(shù)的概念;
 函數(shù)的三要素及表示法,兩個函數(shù)相同的條件;
函數(shù)的三要素及表示法,兩個函數(shù)相同的條件;
 正確理解函數(shù)值的含義,掌握函數(shù)值的求法,會靈活解決有關函數(shù)值的問題;特別是涉及分段函數(shù)或復合函數(shù)的值的問題.
正確理解函數(shù)值的含義,掌握函數(shù)值的求法,會靈活解決有關函數(shù)值的問題;特別是涉及分段函數(shù)或復合函數(shù)的值的問題.
 (
( 北京)過原點作曲線
北京)過原點作曲線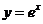 的切線,則切點的坐標為 ,切線的斜率為
的切線,則切點的坐標為 ,切線的斜率為
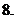 (
(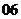 全國)設函數(shù)
全國)設函數(shù) (
(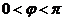 ),若
),若 是奇函數(shù),
是奇函數(shù),
則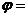
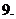 (
( 湖南)設
湖南)設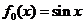 ,
,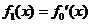 ,
, ,…,
,…,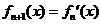 ,
, ,則
,則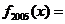
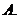
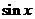
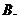

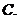


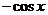
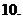 (
(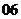 安徽)若曲線
安徽)若曲線 的一條切線
的一條切線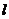 與直線
與直線 垂直,則
垂直,則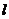 的方程為
的方程為
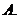
 ;
;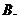
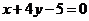 ;
;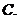
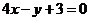 ;
;
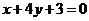
 (
( 海南)曲線
海南)曲線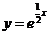 在點
在點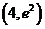 處的切線與坐標軸所圍三角形的面積為
處的切線與坐標軸所圍三角形的面積為
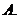

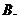

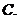
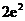

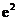
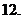 (
(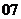 全國Ⅱ文)已知曲線
全國Ⅱ文)已知曲線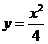 的一條切線的斜率為
的一條切線的斜率為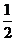 ,則切點的橫坐標為
,則切點的橫坐標為
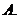

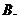
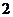
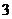


 (
(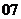 湖北文)已知函數(shù)
湖北文)已知函數(shù)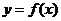 的圖象在點
的圖象在點 處的切線方程是
處的切線方程是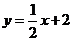 ,則
,則
 (
(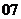 湖北文)曲線
湖北文)曲線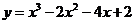 在點
在點 處的切線方程是
處的切線方程是
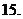 (
(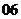 安徽)對正整數(shù)
安徽)對正整數(shù)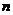 ,設曲線
,設曲線 在
在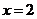 處的切線與
處的切線與 軸交點的縱坐標為
軸交點的縱坐標為 ,則數(shù)列
,則數(shù)列 的前
的前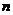 項和的公式是
項和的公式是
 (
(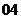 天津)已知函數(shù)
天津)已知函數(shù)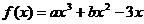 在
在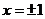 處取得極值.
處取得極值.
 討論
討論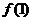 和
和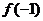 函數(shù)的
函數(shù)的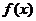 的極大值還是極小值;
的極大值還是極小值;
 過點
過點 作曲線
作曲線 的切線,求此切線方程.
的切線,求此切線方程.
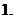 若
若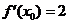 ,求
,求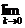

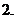 (
(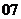 屆高三皖南八校聯(lián)考)已知
屆高三皖南八校聯(lián)考)已知 ,則
,則
 已知
已知 ,則
,則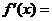
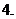 已知函數(shù)
已知函數(shù)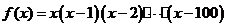 ,則
,則
 (
(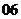 保定市一模)設函數(shù)
保定市一模)設函數(shù)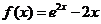 ,則
,則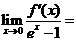
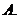
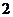
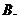

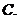
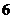
 不存在
不存在
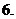 (
( 山東模擬)求下列函數(shù)的導數(shù):
山東模擬)求下列函數(shù)的導數(shù):
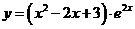 ;
;

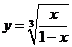
問題1. 已知
已知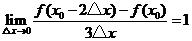 ,求
,求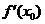
 設函數(shù)
設函數(shù)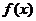 在點
在點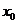 處可導,求
處可導,求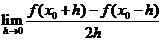
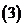 (
( 屆高三寶雞中學第四次月考)已知
屆高三寶雞中學第四次月考)已知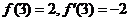 ,
,
則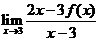 的值為
的值為 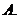

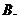
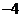
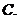
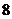
 不存在
不存在
 設
設 ,求
,求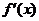 ;
;
 (
(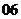 江西)對于
江西)對于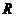 上可導的任意函數(shù)
上可導的任意函數(shù)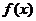 ,若滿足
,若滿足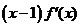 ≥
≥ ,則必有
,則必有
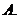
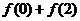
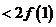
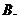
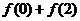 ≤
≤
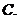
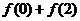 ≥
≥

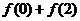

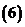 設函數(shù)
設函數(shù)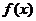 ,
, 在
在 上均可導,且
上均可導,且 ,則當
,則當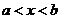 時,有
時,有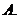
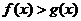
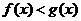
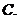
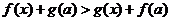


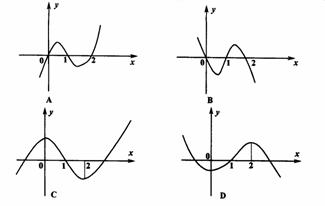
問題2.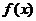 的導函數(shù)
的導函數(shù) 的圖象如圖所示,則
的圖象如圖所示,則 的圖象最有可能的是
的圖象最有可能的是

問題3.求下列函數(shù)的導數(shù):

 ;
;

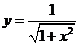 ;
;
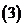
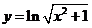 ;
;

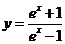 ;
;
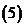
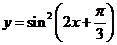 ;
;
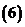


 ;
;
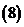


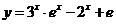
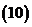
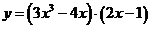
問題4. 求過點
求過點 且與曲線
且與曲線 相切的直線方程.
相切的直線方程.
 (
( 全國Ⅱ文)過點
全國Ⅱ文)過點 作拋物線
作拋物線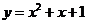 的切線,則其中一條切線為
的切線,則其中一條切線為
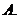
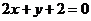
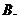
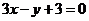
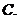



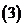 (
( 屆高三攸縣一中)已知曲線
屆高三攸縣一中)已知曲線 的一條切線方程是
的一條切線方程是 ,則
,則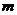
的值為 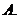
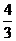
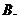
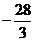
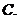
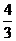 或
或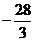

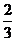 或
或
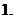 設函數(shù)
設函數(shù) 在
在 處附近有定義,當自變量在
處附近有定義,當自變量在 處有增量
處有增量 時,則函數(shù)
時,則函數(shù)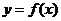 相應地有增量
相應地有增量 ,如果
,如果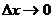 時,
時,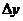 與
與 的比
的比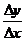 (也叫函數(shù)的平均變化率)有極限即
(也叫函數(shù)的平均變化率)有極限即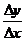 無限趨近于某個常數(shù),我們把這個極限值叫做函數(shù)
無限趨近于某個常數(shù),我們把這個極限值叫做函數(shù) 在
在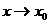 處的導數(shù),記作
處的導數(shù),記作 ,即
,即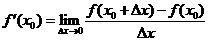
在定義式中,設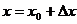 ,則
,則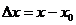 ,當
,當 趨近于
趨近于 時,
時, 趨近于
趨近于 ,因此,導數(shù)的定義式可寫成
,因此,導數(shù)的定義式可寫成
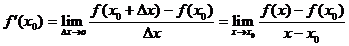 .
.
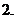 導數(shù)的幾何意義:
導數(shù)的幾何意義:
導數(shù)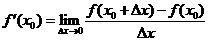 是函數(shù)
是函數(shù) 在點
在點 的處瞬時變化率,它反映的函數(shù)
的處瞬時變化率,它反映的函數(shù) 在點
在點 處變化的快慢程度.
處變化的快慢程度.
它的幾何意義是曲線 上點(
上點( )處的切線的斜率.因此,如果
)處的切線的斜率.因此,如果 在點
在點 可導,則曲線
可導,則曲線 在點(
在點( )處的切線方程為
)處的切線方程為 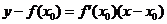
 導函數(shù)(導數(shù)):如果函數(shù)
導函數(shù)(導數(shù)):如果函數(shù) 在開區(qū)間
在開區(qū)間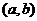 內(nèi)的每點處都有導數(shù),此時對于每一個
內(nèi)的每點處都有導數(shù),此時對于每一個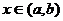 ,都對應著一個確定的導數(shù)
,都對應著一個確定的導數(shù)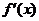 ,從而構(gòu)成了一個新的函數(shù)
,從而構(gòu)成了一個新的函數(shù)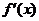 , 稱這個函數(shù)
, 稱這個函數(shù)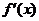 為函數(shù)
為函數(shù) 在開區(qū)間內(nèi)的導函數(shù),簡稱導數(shù),也可記作
在開區(qū)間內(nèi)的導函數(shù),簡稱導數(shù),也可記作 ,即
,即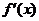 =
= =
=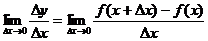
函數(shù) 在
在 處的導數(shù)
處的導數(shù) 就是函數(shù)
就是函數(shù) 在開區(qū)間
在開區(qū)間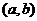
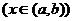 上導數(shù)
上導數(shù)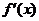 在
在 處的函數(shù)值,即
處的函數(shù)值,即 =
=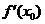 .所以函數(shù)
.所以函數(shù) 在
在 處的導數(shù)也記作
處的導數(shù)也記作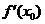

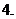 可導: 如果函數(shù)
可導: 如果函數(shù) 在開區(qū)間
在開區(qū)間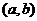 內(nèi)每一點都有導數(shù),則稱函數(shù)
內(nèi)每一點都有導數(shù),則稱函數(shù) 在開區(qū)間
在開區(qū)間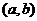 內(nèi)可導
內(nèi)可導
 可導與連續(xù)的關系:如果函數(shù)
可導與連續(xù)的關系:如果函數(shù) 在點
在點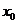 處可導,那么函數(shù)
處可導,那么函數(shù) 在點
在點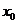 處連續(xù),反之不成立. 函數(shù)具有連續(xù)性是函數(shù)具有可導性的必要條件,而不是充分條件.
處連續(xù),反之不成立. 函數(shù)具有連續(xù)性是函數(shù)具有可導性的必要條件,而不是充分條件.
 求函數(shù)
求函數(shù)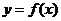 的導數(shù)的一般步驟:
的導數(shù)的一般步驟: 求函數(shù)的改變量
求函數(shù)的改變量
 求平均變化率
求平均變化率 ;
;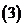 取極限,得導數(shù)
取極限,得導數(shù)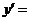

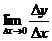
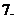 幾種常見函數(shù)的導數(shù):
幾種常見函數(shù)的導數(shù):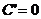 (
(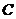 為常數(shù));
為常數(shù));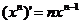 (
(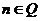 );
);
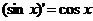 ;
;  ;
;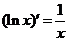 ;
; 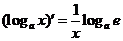 ,
,
 ;
; 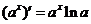
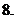 求導法則:法則
求導法則:法則
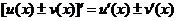 .
.
法則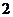
 ,
, 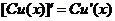
法則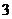 :
: 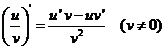
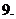 復合函數(shù)的導數(shù):設函數(shù)
復合函數(shù)的導數(shù):設函數(shù) 在點
在點 處有導數(shù)
處有導數(shù) ,函數(shù)
,函數(shù) 在點
在點 的對應點
的對應點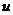 處有導數(shù)
處有導數(shù) ,則復合函數(shù)
,則復合函數(shù) 在點x處也有導數(shù),且
在點x處也有導數(shù),且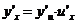 或
或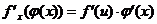
 復合函數(shù)的求導法則:復合函數(shù)對自變量的導數(shù),等于已知函數(shù)對中間變量的導數(shù),乘以中間變量對自變量的導數(shù)
復合函數(shù)的求導法則:復合函數(shù)對自變量的導數(shù),等于已知函數(shù)對中間變量的導數(shù),乘以中間變量對自變量的導數(shù) 
 復合函數(shù)求導的基本步驟是:分解--求導--相乘--回代
復合函數(shù)求導的基本步驟是:分解--求導--相乘--回代
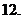 導數(shù)的幾何意義是曲線
導數(shù)的幾何意義是曲線 在點(
在點( )處的切線的斜率,即
)處的切線的斜率,即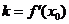 ,
,
要注意“過點 的曲線的切線方程”與“在點
的曲線的切線方程”與“在點 處的切線方程”是不盡相同的,后者
處的切線方程”是不盡相同的,后者 必為切點,前者未必是切點.
必為切點,前者未必是切點.
 (
(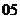 江西)若
江西)若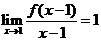 ,則
,則
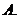

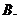

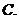
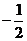

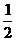
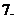 (
(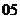 湖北)若
湖北)若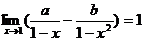 ,則常數(shù)
,則常數(shù) 的值為
的值為
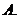

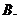
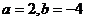
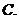
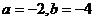

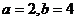
 (
(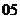 天津)設
天津)設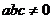 ,
, ,
,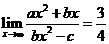 ,則
,則
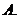

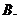

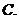
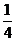

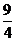
 (
( 四川)
四川)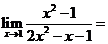
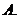
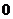
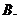

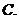
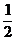

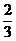
( 江西)
江西)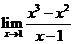
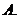 等于
等于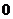
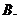 等于
等于
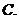 等于
等于
 不存在
不存在
 (
( 天津)設等差數(shù)列
天津)設等差數(shù)列 的公差
的公差 是
是 ,前
,前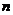 項的和為
項的和為 ,則
,則
 (
( 全國Ⅱ)已知數(shù)列的通項
全國Ⅱ)已知數(shù)列的通項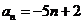 ,其前
,其前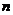 項和為
項和為 ,則
,則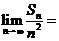
 (
( 湖南)下列四個命題中,不正確的是
湖南)下列四個命題中,不正確的是
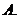 若函數(shù)
若函數(shù) 在
在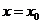 處連續(xù),則
處連續(xù),則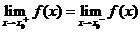
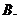 函數(shù)
函數(shù) 的不連續(xù)點是
的不連續(xù)點是 和
和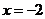
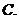 若函數(shù)
若函數(shù) ,
,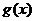 滿足
滿足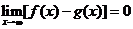 ,則
,則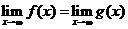

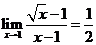
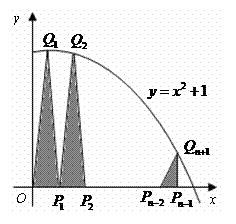
 (
( 安徽)如圖,拋物線
安徽)如圖,拋物線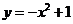 與
與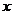 軸的正半軸交于
軸的正半軸交于
點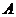 ,將線段
,將線段 的
的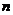 等分點從左至右依次記為
等分點從左至右依次記為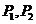 ,…,
,…,
 ,過這些分點分別作
,過這些分點分別作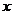 軸的垂線,與拋物線的交點依次為
軸的垂線,與拋物線的交點依次為
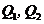 ,…,
,…,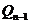 ,從而得到
,從而得到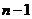 個直角三角形
個直角三角形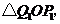
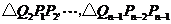 .當
.當 時,這些三角形
時,這些三角形
的面積之和的極限為
 (
( 江西)已知函數(shù)
江西)已知函數(shù)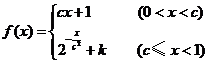 在區(qū)間
在區(qū)間 內(nèi)連續(xù),
內(nèi)連續(xù),
且 .
.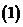 求實數(shù)
求實數(shù) 和
和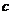 的值;
的值; 解不等式
解不等式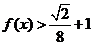 .
.
 (
( 廣東)設函數(shù)
廣東)設函數(shù)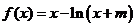 ,其中常數(shù)
,其中常數(shù)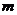 為整數(shù).
為整數(shù).
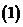 當
當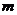 為何值時,
為何值時, ≥
≥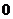 ;
;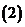 定理:若函數(shù)
定理:若函數(shù)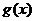 在
在 上連續(xù),且
上連續(xù),且 與
與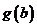 異號,則至少存在一點
異號,則至少存在一點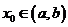 ,使得
,使得 .
.
試用上述定理證明:當整數(shù)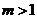 時,方程
時,方程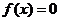 在
在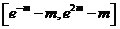 內(nèi)有兩個實根.
內(nèi)有兩個實根.
 已知
已知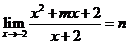 ,求
,求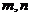 的值.
的值.
 若
若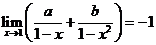 (
( 、
、 為常數(shù)),則
為常數(shù)),則 ;
;
 已知
已知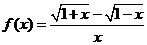 (
( ),那么給
),那么給 一個定義,使
一個定義,使 在
在 處
處
連續(xù),則 應是
應是 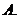
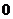
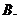

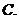


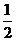
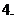 (
( 濟南一模)設
濟南一模)設 是一個一元三次函數(shù)且
是一個一元三次函數(shù)且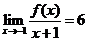 ,
,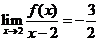 ,
,
則
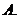

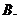

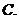
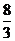


 設函數(shù)
設函數(shù) 在
在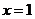 處連續(xù),且
處連續(xù),且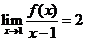 ,則
,則
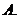

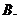
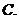
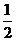


問題1.求下列函數(shù)的極限:
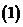
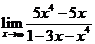 ;
;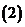
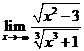 ;
;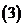
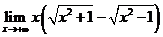 ;
;
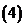
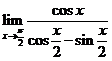 ;
;
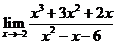 ;
;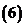
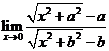 (
( );
);
 (
( 廣東)
廣東)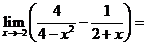
 (
( 陜西)
陜西)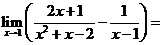
問題2.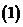 若
若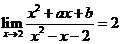 ,求
,求 、
、 的值.
的值.
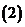 設
設 ,若
,若 ,求常數(shù)
,求常數(shù) 、
、 的值.
的值.
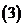 (
( 重慶)設正數(shù)
重慶)設正數(shù)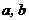 滿足
滿足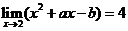 ,則
,則
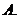
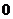
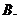
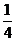
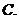
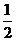


問題3.討論下列函數(shù)在給定點處的連續(xù)性.
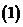
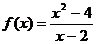 ,點
,點 ;
;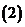
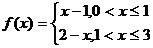 ,點
,點 ;
;
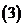 試討論函數(shù)
試討論函數(shù) ,點
,點
問題4. 已知
已知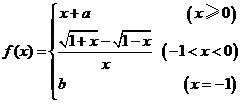 ,在區(qū)間
,在區(qū)間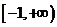 上連續(xù),求
上連續(xù),求
 (
( 屆高三四川眉山市一診)已知函數(shù)
屆高三四川眉山市一診)已知函數(shù) 在
在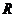 上連續(xù)且單調(diào)遞增,則實數(shù)
上連續(xù)且單調(diào)遞增,則實數(shù)
問題5.已知函數(shù)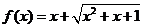 ,
,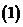 當
當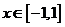 時,求
時,求 的最大值和
的最大值和
最小值;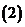 解方程
解方程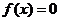 ;
;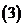 求出該函數(shù)的值域.
求出該函數(shù)的值域.
問題6.證明:方程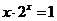 至少有一個小于
至少有一個小于 的正根.
的正根.
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com