
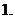 函數(shù)極限的定義:
函數(shù)極限的定義:
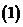 當自變量
當自變量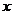 取正值并且無限增大時,如果函數(shù)
取正值并且無限增大時,如果函數(shù) 無限趨近于一個常數(shù)
無限趨近于一個常數(shù) ,就說當
,就說當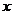 趨向于正無窮大時,函數(shù)
趨向于正無窮大時,函數(shù) 的極限是
的極限是 ,記作:
,記作: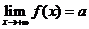 ,或者當
,或者當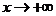 時,
時,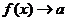 ;
;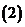 當自變量
當自變量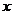 取負值并且絕對值無限增大時,如果函數(shù)
取負值并且絕對值無限增大時,如果函數(shù) 無限趨近于一個常數(shù)
無限趨近于一個常數(shù) ,就說當
,就說當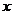 趨向于負無窮大時,函數(shù)
趨向于負無窮大時,函數(shù) 的極限是
的極限是 .
.
記作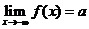 或者當當
或者當當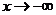 時,
時,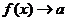
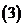 如果
如果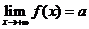 且
且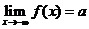 ,那么就說當
,那么就說當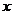 趨向于無窮大時,函數(shù)
趨向于無窮大時,函數(shù) 的極限是
的極限是 ,記作:
,記作: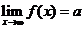 或者當
或者當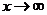 時,
時,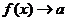 .
.
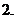 常數(shù)函數(shù):
常數(shù)函數(shù):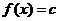 (
(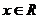 ),有
),有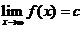 .
.
 存在,表示
存在,表示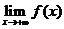 和
和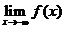 都存在,且兩者相等
都存在,且兩者相等 所以
所以 中的
中的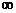 既有
既有 ,又有
,又有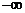 的意義,而數(shù)列極限
的意義,而數(shù)列極限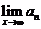 中的
中的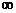 僅有
僅有 的意義.
的意義.
 趨向于定值的函數(shù)極限概念:當自變量
趨向于定值的函數(shù)極限概念:當自變量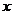 無限趨近于
無限趨近于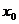 (
( )時,如果函數(shù)
)時,如果函數(shù)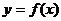 無限趨近于一個常數(shù)
無限趨近于一個常數(shù) ,就說當
,就說當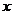 趨向
趨向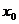 時,函數(shù)
時,函數(shù)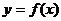 的極限是
的極限是 ,記作
,記作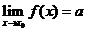 .特別地,
.特別地,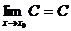 ;
;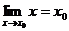 .
.
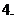
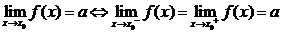 .
.
其中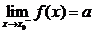 表示當
表示當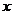 從左側(cè)趨近于
從左側(cè)趨近于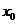 時的左極限,
時的左極限,
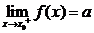 表示當
表示當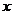 從右側(cè)趨近于
從右側(cè)趨近于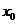 時的右極限.
時的右極限.
 對于函數(shù)極限有如下的運算法則:
對于函數(shù)極限有如下的運算法則:
如果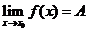 ,
,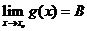 ,那么
,那么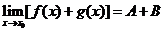 ,
,
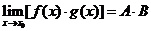 ,
, 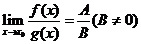 .
.
當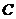 是常數(shù),
是常數(shù),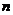 是正整數(shù)時:
是正整數(shù)時: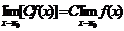 ,
,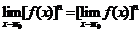
這些法則對于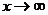 的情況仍然適用.
的情況仍然適用.
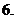 函數(shù)在一點連續(xù)的定義: 如果函數(shù)
函數(shù)在一點連續(xù)的定義: 如果函數(shù) 在點
在點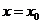 處有定義,
處有定義,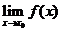 存在,
存在,
且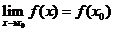 ,那么函數(shù)
,那么函數(shù) 在點
在點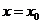 處連續(xù).
處連續(xù).
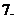 函數(shù)
函數(shù) 在
在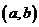 內(nèi)連續(xù)的定義:如果函數(shù)
內(nèi)連續(xù)的定義:如果函數(shù) 在某一開區(qū)間
在某一開區(qū)間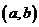 內(nèi)每一點處連續(xù),就說函數(shù)
內(nèi)每一點處連續(xù),就說函數(shù) 在開區(qū)間
在開區(qū)間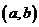 內(nèi)連續(xù),或
內(nèi)連續(xù),或 是開區(qū)間
是開區(qū)間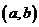 內(nèi)的連續(xù)函數(shù).
內(nèi)的連續(xù)函數(shù).
 函數(shù)
函數(shù) 在
在 上連續(xù)的定義:如果
上連續(xù)的定義:如果 在開區(qū)間
在開區(qū)間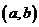 內(nèi)連續(xù),在左端點
內(nèi)連續(xù),在左端點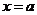 處有
處有 ,在右端點
,在右端點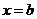 處有
處有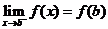 就說函數(shù)
就說函數(shù) 在閉區(qū)間
在閉區(qū)間 上連續(xù),或
上連續(xù),或 是閉區(qū)間
是閉區(qū)間 上的連續(xù)函數(shù).
上的連續(xù)函數(shù).
 最大值:
最大值: 是閉區(qū)間
是閉區(qū)間 上的連續(xù)函數(shù),如果對于任意
上的連續(xù)函數(shù),如果對于任意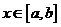 ,
,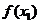 ≥
≥ ,那么
,那么 在點
在點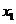 處有最大值
處有最大值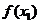 .
.
 最小值:
最小值: 是閉區(qū)間
是閉區(qū)間 上的連續(xù)函數(shù),如果對于任意
上的連續(xù)函數(shù),如果對于任意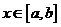 ,
,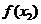 ≤
≤ ,那么
,那么 在點
在點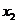 處有最小值
處有最小值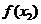 .
.
 最大值最小值定理
最大值最小值定理
如果 是閉區(qū)間
是閉區(qū)間 上的連續(xù)函數(shù),那么
上的連續(xù)函數(shù),那么 在閉區(qū)間
在閉區(qū)間 上有最大值和最小值.
上有最大值和最小值.
 極限問題的基本類型:分式型,主要看分子和分母的首項系數(shù);
極限問題的基本類型:分式型,主要看分子和分母的首項系數(shù);
指數(shù)型(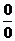 和
和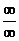 型),通過變形使得各式有極限;
型),通過變形使得各式有極限;
根式型(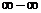 型),通過有理化變形使得各式有極限;
型),通過有理化變形使得各式有極限;
 根的存在定理:若①函數(shù)
根的存在定理:若①函數(shù) 在
在 上連續(xù),②
上連續(xù),②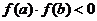 ,則方程
,則方程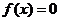 至少有一根在區(qū)間
至少有一根在區(qū)間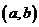 內(nèi);若①函數(shù)
內(nèi);若①函數(shù) 在
在 上連續(xù)且單調(diào),②
上連續(xù)且單調(diào),②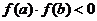 ,則方程
,則方程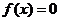 有且只有一根在區(qū)間
有且只有一根在區(qū)間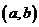 內(nèi).
內(nèi).
 (
( 重慶)
重慶)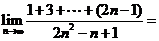
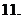 (
(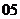 上海)計算:
上海)計算: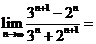
 (
(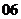 上海)計算:
上海)計算: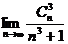 =
=
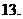 (
(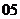 湖南)已知數(shù)列
湖南)已知數(shù)列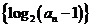 (
(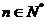 )為等差數(shù)列,且
)為等差數(shù)列,且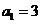 ,
, ,
,
則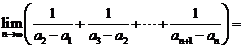
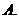

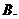
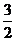
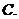
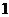
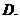
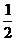
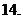 (
( 湖北)已知不等式
湖北)已知不等式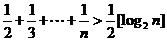 ,其中
,其中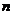 為大于
為大于 的整數(shù),
的整數(shù),
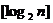 表示不超過
表示不超過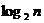 的最大整數(shù). 設(shè)數(shù)列
的最大整數(shù). 設(shè)數(shù)列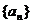 的各項為正,且滿足
的各項為正,且滿足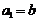
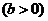 ,
,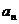 ≤
≤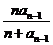 ,
,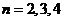 ,…
,…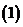 證明
證明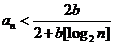 ,
,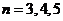 ,…
,…
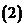 猜測數(shù)列
猜測數(shù)列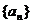 是否有極限?如果有,寫出極限的值(不必證明);
是否有極限?如果有,寫出極限的值(不必證明);
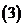 )試確定一個正整數(shù)
)試確定一個正整數(shù)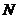 ,使得當
,使得當 時,對任意
時,對任意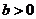 ,都有
,都有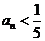 .
.
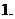 將
將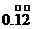 化成分數(shù)是
化成分數(shù)是
 若
若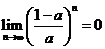 ,則
,則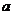 的取值范圍是
的取值范圍是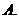
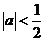
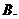
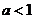
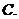
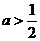
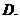
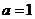
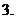
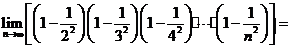
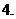
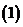
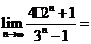 ;
;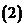
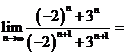
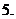 已知
已知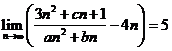 ,則
,則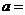 ;
;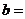 ;
;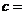
 (
(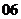 湖北宜昌市
湖北宜昌市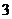 月模擬)已知數(shù)列
月模擬)已知數(shù)列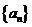 滿足
滿足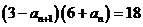 (
(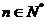 ),
),
且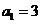 ,則
,則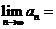
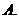

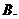
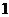
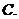
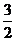
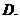
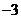
 (
(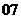 屆高三湖北八校聯(lián)考)已知數(shù)列
屆高三湖北八校聯(lián)考)已知數(shù)列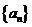 的前
的前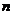 項和
項和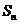 滿足
滿足 ,則其各項和
,則其各項和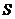 等于
等于
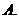
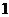
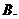
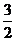
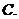
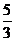
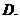
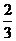
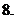 若數(shù)列
若數(shù)列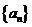 的通項公式是
的通項公式是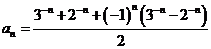 ,
,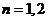 ,…,
,…,
則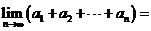
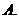
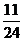
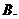

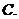

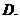
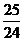
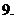 數(shù)列
數(shù)列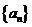 中,
中,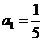 ,
,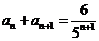 ,
,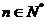 ,則
,則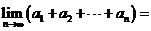
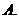
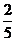
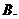
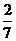
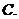
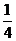
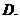
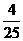
、
問題1.求下列數(shù)列的極限: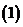
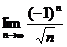 ;
; 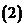
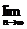
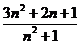 ;
; 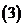
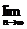
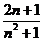
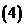

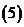
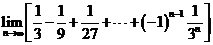
問題2.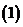 (
(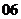 陜西)
陜西)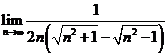 等于
等于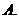
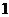
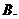
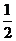
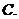
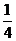
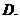

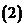 (
(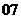 天津)設(shè)等差數(shù)列
天津)設(shè)等差數(shù)列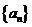 的公差
的公差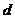 是
是 ,前
,前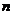 項的和為
項的和為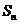 ,則
,則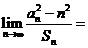
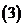 (
(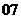 湖北)已知
湖北)已知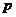 和
和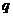 是兩個不相等的正整數(shù),且
是兩個不相等的正整數(shù),且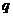 ≥
≥ ,則
,則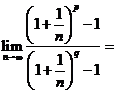

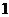
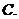
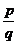
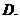
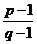
問題3.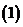 若
若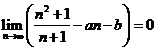 ,求
,求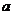 和
和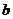 的值;
的值;
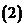 若
若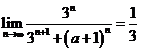 ,求
,求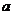 的取值范圍.
的取值范圍.
問題4.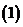 已知數(shù)列
已知數(shù)列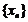 滿足
滿足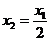 ,
, ,
,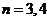 ,… ,
,… ,
若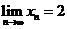 ,則
,則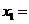
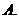
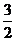
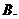
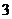
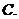
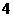
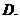
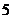
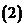 已知
已知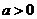 ,數(shù)列
,數(shù)列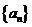 滿足
滿足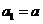 ,
,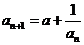 (
(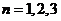 ,…),且數(shù)列
,…),且數(shù)列 的極限存在,則
的極限存在,則 (結(jié)果用
(結(jié)果用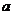 表示).
表示).
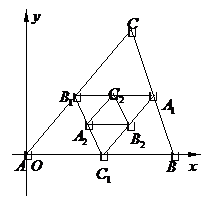 問題5.(
問題5.(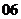 福建)如圖,連結(jié)
福建)如圖,連結(jié)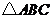 的各邊中點
的各邊中點
得到一個新的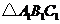 又連結(jié)
又連結(jié)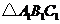 的各邊中點得
的各邊中點得
到 ,如此無限繼續(xù)下去,得到一系列三角形:
,如此無限繼續(xù)下去,得到一系列三角形:
 ,
, ,
, ,…,這一系列
,…,這一系列
三角形趨向于一個點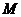 .已知
.已知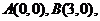
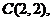
則點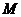 的坐標是
的坐標是
 數(shù)列極限的定義:
數(shù)列極限的定義:
一般地,如果當項數(shù)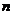 無限增大時,無窮數(shù)列
無限增大時,無窮數(shù)列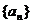 的項
的項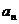 無限趨近于某個常數(shù)
無限趨近于某個常數(shù)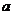
(即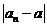 無限地接近于
無限地接近于 ),那么就說數(shù)列
),那么就說數(shù)列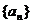 以
以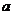 為極限.記作
為極限.記作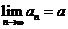 .
.
注: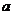 不一定是
不一定是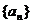 中的項
中的項
 幾個重要極限:
幾個重要極限: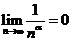 (
(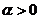 ,
,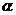 為常數(shù));
為常數(shù)); 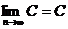 (
(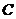 是常數(shù));
是常數(shù));
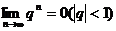 ;
;
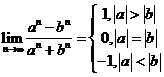
 極限問題的基本類型:分式型,主要看分子和分母的首項系數(shù);
極限問題的基本類型:分式型,主要看分子和分母的首項系數(shù);
指數(shù)型(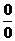 和
和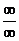 型),通過變形(如通分,約分)使得各式有極限;
型),通過變形(如通分,約分)使得各式有極限;
根式型(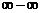 型),通過有理化變形使得各式有極限;
型),通過有理化變形使得各式有極限;
 數(shù)列極限的運算法則:與函數(shù)極限的運算法則類似, 如果
數(shù)列極限的運算法則:與函數(shù)極限的運算法則類似, 如果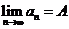 ,
,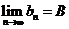 ,那么
,那么
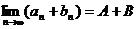
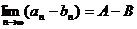
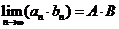
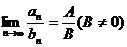 .
.
特別地,如果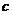 是常數(shù),那么,
是常數(shù),那么,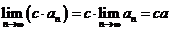
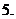 無窮等比數(shù)列的各項和:
無窮等比數(shù)列的各項和: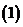 公比的絕對值小于
公比的絕對值小于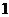 的無窮等比數(shù)列前
的無窮等比數(shù)列前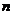 項的和當
項的和當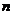 無限增大時的極限,叫做這個無窮等比數(shù)列各項的和,記做
無限增大時的極限,叫做這個無窮等比數(shù)列各項的和,記做 ;
;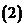
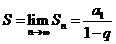
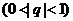
 (
( 上海)設(shè)
上海)設(shè) 是定義在正整數(shù)集上的函數(shù),且
是定義在正整數(shù)集上的函數(shù),且 滿足:“當
滿足:“當 成立時,總可推出
成立時,總可推出
 成立”.那么,下列命題總成立的是
成立”.那么,下列命題總成立的是
 若
若 成立,則當
成立,則當 時,均有
時,均有 成立
成立
 若
若 成立,則當
成立,則當 時,均有
時,均有 成立
成立
 若
若 成立,則當
成立,則當 時,均有
時,均有 成立
成立
 若
若 成立,則當
成立,則當 時,均有
時,均有 成立
成立
 (
( 湖南)已知函數(shù)
湖南)已知函數(shù) ,數(shù)列{
,數(shù)列{ }滿足:
}滿足:
 ,
, ,
, 求證:
求證:
 ;
;
 .
.
 (
( 江西)已知數(shù)列
江西)已知數(shù)列 滿足:
滿足: ,且
,且 (
( ≥
≥ ,
, )
)
 求數(shù)列
求數(shù)列 的通項公式;
的通項公式; 求證:對于一切正整數(shù)
求證:對于一切正整數(shù) ,不等式
,不等式
 (
( 湖北)已知
湖北)已知 為正整數(shù),
為正整數(shù),
 用數(shù)學歸納法證明:當
用數(shù)學歸納法證明:當 時,
時, ≥
≥ ;
;
 對于
對于 ≥
≥ ,已知
,已知 ,求證
,求證 ,
, ;
;
 求出滿足等式
求出滿足等式 的所有正整數(shù)
的所有正整數(shù) .
.
 觀察下列式子:
觀察下列式子: ,則可以猜想的結(jié)論為:
,則可以猜想的結(jié)論為:
 用數(shù)學歸納法證明“
用數(shù)學歸納法證明“ ”,從“
”,從“ 到
到 ”左端需增乘的代數(shù)式為
”左端需增乘的代數(shù)式為








 (
( 重慶市重點中學二聯(lián))
重慶市重點中學二聯(lián)) 如圖,第
如圖,第 個圖形是由正
個圖形是由正 邊形“擴展”而來(
邊形“擴展”而來( ,
, ,
, ,…),則第
,…),則第 個圖形中共有
個頂點.
個圖形中共有
個頂點.

 凸
凸 邊形有
邊形有 條對角線,則凸
條對角線,則凸 邊形有對角線條數(shù)
邊形有對角線條數(shù) 為
為








 平面內(nèi)有
平面內(nèi)有 條直線,其中任何兩條不平行,任何三條不共點,求證:這
條直線,其中任何兩條不平行,任何三條不共點,求證:這 條直線把平面分成
條直線把平面分成 個區(qū)域.
個區(qū)域.
問題1.求證: 能被
能被 整除.
整除.
問題2. 求證:
求證:
 設(shè)
設(shè) ,且
,且 ,用數(shù)學歸納法證明:
,用數(shù)學歸納法證明:
 用數(shù)學歸納法證明:
用數(shù)學歸納法證明: (其中
(其中 ≥
≥ ,且
,且 ).
).
問題3.已知 ,
, ,其中
,其中 、
、 ,
, ,
, ,
, ,且
,且 .
. 求
求 的反函數(shù)
的反函數(shù) ;
; 對任意
對任意 ,試指出
,試指出 與
與 的大小關(guān)系,并證明你的結(jié)論.
的大小關(guān)系,并證明你的結(jié)論.
問題4.( 浙江)設(shè)點
浙江)設(shè)點 ,
, 和拋物線
和拋物線 :
: (
( ),其中
),其中 =
= ,
, 由以下方法得到:
由以下方法得到: ,點
,點 在拋物線
在拋物線 :
: 上,點
上,點 到
到 的距離是
的距離是 到
到 上點的最短距離,…,點
上點的最短距離,…,點 在拋物線
在拋物線 :
: 上,點
上,點 到
到 的距離是
的距離是 到
到 上點的最短距離.
上點的最短距離.  求
求 及
及 的方程;
的方程; 證明
證明 是等差數(shù)列.
是等差數(shù)列.
 歸納法:由一些特殊事例推出一般結(jié)論的推理方法
歸納法:由一些特殊事例推出一般結(jié)論的推理方法 特點:特殊→一般.
特點:特殊→一般.
 不完全歸納法: 根據(jù)事物的部分(而不是全部)特例得出一般結(jié)論的推理方法叫做不完全歸納法
不完全歸納法: 根據(jù)事物的部分(而不是全部)特例得出一般結(jié)論的推理方法叫做不完全歸納法
 完全歸納法: 把研究對象一一都考查到了而推出結(jié)論的歸納法稱為完全歸納法
完全歸納法: 把研究對象一一都考查到了而推出結(jié)論的歸納法稱為完全歸納法
完全歸納法是一種在研究了事物的所有(有限種)特殊情況后得出一般結(jié)論的推理方法,又叫做枚舉法.與不完全歸納法不同,用完全歸納法得出的結(jié)論是可靠的 通常在事物包括的特殊情況數(shù)不多時,采用完全歸納法
通常在事物包括的特殊情況數(shù)不多時,采用完全歸納法
 數(shù)學歸納法:對于某些與自然數(shù)
數(shù)學歸納法:對于某些與自然數(shù) 有關(guān)的命題常常采用下面的方法來證明它的正確性:先證明當
有關(guān)的命題常常采用下面的方法來證明它的正確性:先證明當 取第一個值
取第一個值 時命題成立;然后假設(shè)當
時命題成立;然后假設(shè)當 (
( ,
, ≥
≥ )時命題成立,證明當
)時命題成立,證明當 命題也成立
命題也成立 這種證明方法就叫做數(shù)學歸納法.
這種證明方法就叫做數(shù)學歸納法.
 數(shù)學歸納法的基本思想:即先驗證使結(jié)論有意義的最小的正整數(shù)
數(shù)學歸納法的基本思想:即先驗證使結(jié)論有意義的最小的正整數(shù) ,如果當
,如果當 時,命題成立,再假設(shè)當
時,命題成立,再假設(shè)當 (
( ,
, ≥
≥ )時,命題成立.(這時命題是否成立不是確定的),根據(jù)這個假設(shè),如能推出當
)時,命題成立.(這時命題是否成立不是確定的),根據(jù)這個假設(shè),如能推出當 時,命題也成立,那么就可以遞推出對所有不小于
時,命題也成立,那么就可以遞推出對所有不小于 的正整數(shù)
的正整數(shù) ,
, ,…,命題都成立.
,…,命題都成立.
 用數(shù)學歸納法證明一個與正整數(shù)有關(guān)的命題的步驟:
用數(shù)學歸納法證明一個與正整數(shù)有關(guān)的命題的步驟:
 證明:當
證明:當 取第一個值
取第一個值 結(jié)論正確;
結(jié)論正確; 假設(shè)當
假設(shè)當 (
( ,
, ≥
≥ )時結(jié)論正確,證明當
)時結(jié)論正確,證明當 時結(jié)論也正確
時結(jié)論也正確 由
由 ,
, 可知,命題對于從
可知,命題對于從 開始的所有正整數(shù)
開始的所有正整數(shù) 都正確.數(shù)學歸納法被用來證明與自然數(shù)有關(guān)的命題:遞推基礎(chǔ)不可少,歸納假設(shè)要用到,結(jié)論寫明莫忘掉.
都正確.數(shù)學歸納法被用來證明與自然數(shù)有關(guān)的命題:遞推基礎(chǔ)不可少,歸納假設(shè)要用到,結(jié)論寫明莫忘掉.

 用數(shù)學歸納法證題時,兩步缺一不可;
用數(shù)學歸納法證題時,兩步缺一不可; 證題時要注意兩湊:一湊歸納假設(shè),二湊目標.
證題時要注意兩湊:一湊歸納假設(shè),二湊目標.
 (
( 四川)甲校有
四川)甲校有 名學生,乙校有
名學生,乙校有 名學生,丙校有
名學生,丙校有 名學生,為統(tǒng)計三校學生某方面的情況,計劃采用分層抽樣法,抽取一個樣本容量為
名學生,為統(tǒng)計三校學生某方面的情況,計劃采用分層抽樣法,抽取一個樣本容量為 人的樣本,應(yīng)在這三校分別抽取學生
人的樣本,應(yīng)在這三校分別抽取學生

 人,
人, 人,
人, 人
人 
 人,
人, 人,
人, 人
人

 人,
人, 人,
人, 人
人 
 人,
人, 人,
人, 人
人
 (
( 天津) 某工廠生產(chǎn)
天津) 某工廠生產(chǎn) 、
、 、
、 三種不同型號的產(chǎn)品,產(chǎn)品數(shù)量之比依次為
三種不同型號的產(chǎn)品,產(chǎn)品數(shù)量之比依次為 ,現(xiàn)用分層抽樣方法抽出一個容量為
,現(xiàn)用分層抽樣方法抽出一個容量為 的樣本,樣本中
的樣本,樣本中 種型號產(chǎn)品有
種型號產(chǎn)品有 件.那么此樣本的容量
件.那么此樣本的容量
 (
( 陜西文)某商場有四類食品,其中糧食類、植物油類、動物性食品類及果蔬類分別有
陜西文)某商場有四類食品,其中糧食類、植物油類、動物性食品類及果蔬類分別有 種、
種、 種、
種、 種、
種、 種,現(xiàn)從中抽取一個容量為
種,現(xiàn)從中抽取一個容量為 的樣本進行食品安全檢測。若采用分層抽樣的方法抽取樣本,則抽取的植物油類與果蔬類食品種數(shù)之和是( )
的樣本進行食品安全檢測。若采用分層抽樣的方法抽取樣本,則抽取的植物油類與果蔬類食品種數(shù)之和是( ) 







 (
( 全國Ⅰ文)從某自動包裝機包裝的食鹽中,隨機抽取
全國Ⅰ文)從某自動包裝機包裝的食鹽中,隨機抽取 袋,測得各袋的質(zhì)量分別為(單位:
袋,測得各袋的質(zhì)量分別為(單位: ):
):
|
492 |
496 |
494 |
495 |
498 |
497 |
501 |
502 |
504 |
496 |
|
497 |
503 |
506 |
508 |
507 |
492 |
496 |
500 |
501 |
499 |
根據(jù)頻率分布估計總體分布的原理,該自動包裝機包裝的袋裝食鹽質(zhì)量在 -
- 之間的概率約為
之間的概率約為
 (
( 湖北)某初級中學有學生
湖北)某初級中學有學生 人,其中一年級
人,其中一年級 人,二、三年級各
人,二、三年級各 人,現(xiàn)要利用抽樣方法抽取
人,現(xiàn)要利用抽樣方法抽取 人參加某項調(diào)查,考慮選用簡單隨機抽樣、分層抽樣和系統(tǒng)抽樣三種方案,使用簡單隨機抽樣和分層抽樣時,將學生按一、二、三年級依次統(tǒng)一編號為
人參加某項調(diào)查,考慮選用簡單隨機抽樣、分層抽樣和系統(tǒng)抽樣三種方案,使用簡單隨機抽樣和分層抽樣時,將學生按一、二、三年級依次統(tǒng)一編號為 ,
, ,…,
,…, ;使用系統(tǒng)抽樣時,將學生統(tǒng)一隨機編號
;使用系統(tǒng)抽樣時,將學生統(tǒng)一隨機編號 ,
, ,…,
,…, ,并將整個編號依次分為
,并將整個編號依次分為 段.如果抽得號碼有下列四種情況:
段.如果抽得號碼有下列四種情況:
① ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ;
;
② ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ;
;
③ ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ;
;
④ ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ;
;
關(guān)于上述樣本的下列結(jié)論中,正確的是
 ②、③都不能為系統(tǒng)抽樣
②、③都不能為系統(tǒng)抽樣  ②、④都不能為分層抽樣
②、④都不能為分層抽樣
 ①、④都可能為系統(tǒng)抽樣
①、④都可能為系統(tǒng)抽樣  ①、③都可能為分層抽樣
①、③都可能為分層抽樣
 (
( 湖南)設(shè)隨機變量
湖南)設(shè)隨機變量 服從標準正態(tài)分布
服從標準正態(tài)分布 ,已知
,已知 ,
,
則








 (
( 福建)兩封信隨機投入
福建)兩封信隨機投入 三個空郵箱,則
三個空郵箱,則 郵箱的信件數(shù)
郵箱的信件數(shù) 的數(shù)學期望
的數(shù)學期望
 (
( 浙江)已知隨機變量
浙江)已知隨機變量 服從正態(tài)分布
服從正態(tài)分布 ,
,
 ,
,
則








 (
( 全國Ⅱ)在某項測量中,測量結(jié)果
全國Ⅱ)在某項測量中,測量結(jié)果 服從正態(tài)分布
服從正態(tài)分布
 .若
.若 在
在 內(nèi)取值的概率為
內(nèi)取值的概率為 ,則
,則 在
在 內(nèi)取值的概率為
內(nèi)取值的概率為
 (
( 屆高三浙江嘉興市二檢)已知隨機變量
屆高三浙江嘉興市二檢)已知隨機變量 ,若
,若 ,則
,則








 (
( 遼寧文)某公司在過去幾年內(nèi)使用某種型號的燈管
遼寧文)某公司在過去幾年內(nèi)使用某種型號的燈管 支,該公司對這些燈管的使用壽命(單位:小時)進行了統(tǒng)計,統(tǒng)計結(jié)果如下表所示:
支,該公司對這些燈管的使用壽命(單位:小時)進行了統(tǒng)計,統(tǒng)計結(jié)果如下表所示:
|
分組 |
[500,900) |
[900,1100) |
[1100,1300) |
[1300,1500) |
[1500,1700) |
[1700,1900) |
[1900, ) ) |
|
頻數(shù) |
 |
 |
 |
 |
 |
 |
 |
|
頻率 |
|
|
|
|
|
|
|
 將各組的頻率填入表中;
將各組的頻率填入表中;
 根據(jù)上述統(tǒng)計結(jié)果,計算燈管使用壽命不足
根據(jù)上述統(tǒng)計結(jié)果,計算燈管使用壽命不足 小時的頻率;
小時的頻率;
 該公司某辦公室新安裝了這種型號的燈管
該公司某辦公室新安裝了這種型號的燈管 支,若將上述頻率作為概率,試求至少有
支,若將上述頻率作為概率,試求至少有 支燈管的使用壽命不足
支燈管的使用壽命不足 小時的概率.
小時的概率.
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com