
 (
( 湖南)棱長為
湖南)棱長為 的正方體
的正方體 的
的 個頂點都在球
個頂點都在球 的表面上,
的表面上, 分別是棱
分別是棱 ,
, 的中點,則直線
的中點,則直線 被球
被球 截得的線段長為
截得的線段長為








 .(
.( 安徽文)把邊長為
安徽文)把邊長為 的正方形
的正方形 沿對角線
沿對角線 折成直二面角,折成直二面角后,在
折成直二面角,折成直二面角后,在 四點所在的球面上,
四點所在的球面上, 與
與 兩點之間的球面距離為
兩點之間的球面距離為









 (
( 江西)如圖,正方體
江西)如圖,正方體 的棱長為
的棱長為 ,過點
,過點 作平面
作平面 的垂線,垂足為點
的垂線,垂足為點 ,則以下命題中,錯誤的命題是
,則以下命題中,錯誤的命題是
 點
點 是
是 的垂心
的垂心

 垂直平面
垂直平面

 的延長線經過點
的延長線經過點
 直線
直線 和
和 所成角為
所成角為

 (
( 天津)如圖,在斜三棱柱
天津)如圖,在斜三棱柱 中,
中,
 ,
, ,
, ,
,
側面 與底面
與底面 所成的二面角為
所成的二面角為 ,
,
 分別是棱
分別是棱 、
、 的中點.
的中點.
 求
求 與底面
與底面 所成的角;
所成的角;
 證明:
證明: ∥平面
∥平面 ;
;
 求經過
求經過 四點的球的體積.
四點的球的體積.
 將正方形折成正四棱柱的側面,正方形的對角線
將正方形折成正四棱柱的側面,正方形的對角線 被折成折線
被折成折線 ,則
,則
為定值
 有一個長方體形的水泥構件
有一個長方體形的水泥構件 ,其中
,其中 ,
, ,
, ,
,
現在小螞蟻要從點 沿表面到放有食物的
沿表面到放有食物的 點,則小螞蟻需走的最短路線長為
點,則小螞蟻需走的最短路線長為








 已知體積為
已知體積為 的正三棱錐
的正三棱錐 的外接球
的外接球 的半徑是
的半徑是 ,且滿足
,且滿足 ,則其外接球
,則其外接球 的表面積是
(用含
的表面積是
(用含 及數字作答,不能含
及數字作答,不能含 )
)
 如果
如果 是線段
是線段 上一點,則
上一點,則 ;類比到平面的情形:若
;類比到平面的情形:若 是
是 內一點,有
內一點,有 ;類比到空間的情形:若
;類比到空間的情形:若
是四面體 內一點,則有
內一點,則有
 三棱錐
三棱錐 的
的 條棱中,其中
條棱中,其中 條棱的長都是
條棱的長都是 ,則第
,則第 條棱長的取值范圍是
條棱長的取值范圍是









 (
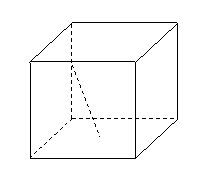
( 屆高三湖北八校月考)如圖,
屆高三湖北八校月考)如圖, 所在的平面
所在的平面 和
和
四邊形 所在的平面
所在的平面 垂直,且
垂直,且 ,
, ,
,
 ,
, ,
, ,
, ,則點
,則點
在平面 內的軌跡是
內的軌跡是
 圓的一部分
圓的一部分
 橢圓的一部分
橢圓的一部分
 雙曲線的一部分
雙曲線的一部分
 拋物線的一部分
拋物線的一部分

 (
( 屆高三安徽省江南十校聯考)如圖,已知正方體
屆高三安徽省江南十校聯考)如圖,已知正方體
 的棱長為
的棱長為 ,長為
,長為 的線段
的線段 的
的
一個端點 在棱
在棱 上運動,點
上運動,點 在正方形
在正方形
內運動,則 中點
中點 的軌跡的面積為
的軌跡的面積為








 四面體的一條棱長為
四面體的一條棱長為 ,其它各棱長為
,其它各棱長為 ,若將四面體的體積
,若將四面體的體積 表示為
表示為 的函數
的函數 ,則函數
,則函數 的單調遞減區間為
的單調遞減區間為







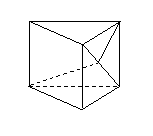 問題1. (
問題1. ( 江西)如圖,在直三棱柱
江西)如圖,在直三棱柱 中,底面為直角三角形,
中,底面為直角三角形, ,
, ,
, ,
, 是
是 上一動點,則
上一動點,則 的最小值
的最小值
是
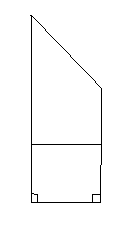
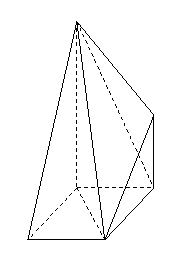 問題2.將如圖
問題2.將如圖 所示的直角梯形
所示的直角梯形 (圖中所示數字為對應線段長度)沿直線
(圖中所示數字為對應線段長度)沿直線 折成直二面角,連結部分線段后圍成一個空間幾何體,如圖
折成直二面角,連結部分線段后圍成一個空間幾何體,如圖 所示,
所示, 求異面直線
求異面直線 與
與 所成角的大小;
所成角的大小; 求二面角
求二面角 的大小;
的大小;
 這五個點在同一球面上,求該球的表面積.
這五個點在同一球面上,求該球的表面積.
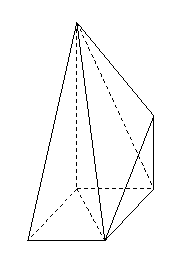
問題3.( 江西)右圖是一個直三棱柱(以
江西)右圖是一個直三棱柱(以 為底面)被一平面所截得到的
為底面)被一平面所截得到的
 幾何體,截面為
幾何體,截面為 .已知
.已知 ,
, ,
, ,
, ,
, .
. 設點
設點 是
是 的中點,證明:
的中點,證明: ∥平面
∥平面
 求二面角
求二面角 的大小;
的大小;
 求此幾何體的體積 .
求此幾何體的體積 .
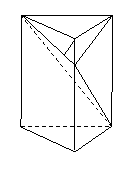
 問題4. (
問題4. ( 重慶)如圖,在直三棱柱
重慶)如圖,在直三棱柱 中,
中,
 ,
, ,
, ;點
;點 分別在
分別在 ,
,
 上,且
上,且 ,四棱錐
,四棱錐 與直三棱柱的
與直三棱柱的
體積之比為 .
. 求異面直線
求異面直線 與
與 的距離;
的距離;
 若
若 ,求二面角
,求二面角 的平面角的正切值.
的平面角的正切值.
折疊問題的計算與證明: 一定要關注“變量”和“不變量”在證明和計算中的應用:折疊時位于棱同側的位置關系和數量關系不變;位于棱兩側的位置關系與數量關系變,
一定要關注“變量”和“不變量”在證明和計算中的應用:折疊時位于棱同側的位置關系和數量關系不變;位于棱兩側的位置關系與數量關系變, 折前折后的圖形結合起來使用.
折前折后的圖形結合起來使用.
 (
( 陜西)一個正三棱錐的四個頂點都在半徑為
陜西)一個正三棱錐的四個頂點都在半徑為 的球面上,其中底面的三個頂點在該球的一個大圓上,則該正三棱錐的體積是
的球面上,其中底面的三個頂點在該球的一個大圓上,則該正三棱錐的體積是 







 (
( 遼寧)若一個底面邊長為
遼寧)若一個底面邊長為 ,棱長為
,棱長為 的正六棱柱的所有頂點都在一個平面上,則此球的體積為
的正六棱柱的所有頂點都在一個平面上,則此球的體積為
 (
( 全國Ⅱ)一個正四棱柱的各個頂點在一個直徑為
全國Ⅱ)一個正四棱柱的各個頂點在一個直徑為 的球面上。如果正四棱柱的底面邊長為
的球面上。如果正四棱柱的底面邊長為 ,那么該棱柱的表面積為
,那么該棱柱的表面積為

 正方體、正多面體、凸多面體、簡單多面體是什么關系?
正方體、正多面體、凸多面體、簡單多面體是什么關系?
 已知凸多面體每個面都是五邊形,每個頂點都有三條棱相交,試求該凸多面體的面數、頂點數和棱數.
已知凸多面體每個面都是五邊形,每個頂點都有三條棱相交,試求該凸多面體的面數、頂點數和棱數.
 一個廣告氣球被一束入射角為
一個廣告氣球被一束入射角為 的平行光線照射,其投影是一個長半軸為
的平行光線照射,其投影是一個長半軸為 的橢圓,則制作這個廣告氣球至少需要的面料是
的橢圓,則制作這個廣告氣球至少需要的面料是
 在球面上有四個點
在球面上有四個點 、
、 、
、 、
、 ,如果
,如果 、
、 、
、 兩兩互相垂直,且
兩兩互相垂直,且 ,那么這個球面的面積是
,那么這個球面的面積是 







 北緯
北緯 的圓把北半球面積分為兩部分,這兩部分面積的比為
的圓把北半球面積分為兩部分,這兩部分面積的比為








 已知過球面上
已知過球面上 、
、 、
、 三點的截面和球心的距離等于球半徑的一半,
三點的截面和球心的距離等于球半徑的一半,
且 ,則球面面積是
,則球面面積是








 正八面體的相鄰兩個面所成二面角的大小為
正八面體的相鄰兩個面所成二面角的大小為








問題1. (
( 遼寧)棱長為
遼寧)棱長為 的正方體,連結相鄰面的中心,以這些線段為棱的
的正方體,連結相鄰面的中心,以這些線段為棱的
八面體的體積為 







 已知一個正四面體和一個正八面體的棱長相等且為
已知一個正四面體和一個正八面體的棱長相等且為 ,把它們拼起來,使一個表面重合,所得的多面體有多少個面?
,把它們拼起來,使一個表面重合,所得的多面體有多少個面?
問題2. (
( 天津)一個長方體的各頂點均在同一球的球面上,且一個頂點上的三條棱的長分別為
天津)一個長方體的各頂點均在同一球的球面上,且一個頂點上的三條棱的長分別為 ,則此球的表面積為
,則此球的表面積為
 (
( 全國Ⅰ文)正四棱錐
全國Ⅰ文)正四棱錐 的底面邊長和各側棱長都為
的底面邊長和各側棱長都為 ,點
,點
都在同一個球面上,則該球的體積為
 (
( 江西文)四面體
江西文)四面體 的外接球球心在
的外接球球心在 上,且
上,且 ,
, ,
,
在外接球面上兩點 、
、 間的球面距離是
間的球面距離是 







 (
( 陜西)水平桌面
陜西)水平桌面 上放有
上放有 個半徑均為
個半徑均為 的球,且相鄰的球都相切(球心的連線構成正方形).在這
的球,且相鄰的球都相切(球心的連線構成正方形).在這 個球的上面放
個球的上面放 個半徑為
個半徑為 的小球,它和下面
的小球,它和下面 個球恰好都相切,則小球的球心到水平桌面
個球恰好都相切,則小球的球心到水平桌面 的距離是
的距離是
 問題3. (
問題3. ( 四川)設球
四川)設球 的半徑是
的半徑是 ,
, 、
、 、
、 是球面上三點,已知
是球面上三點,已知 到
到 、
、 兩點的球面距離都是
兩點的球面距離都是 ,且二面角
,且二面角 的大小為
的大小為 ,則從
,則從 點沿球面經
點沿球面經 、
、 兩點再回到
兩點再回到 點的最短距離是
點的最短距離是








問題4.三棱錐 的兩條棱
的兩條棱 ,其余各棱長均為
,其余各棱長均為 ,求三棱錐的內切球半徑和外接球半徑.
,求三棱錐的內切球半徑和外接球半徑.
問題5.已知球的半徑為 ,在球內作一個內接圓柱,這個圓柱底面半徑與高為何值時,它的側面積最大?側面積的最大值是多少?
,在球內作一個內接圓柱,這個圓柱底面半徑與高為何值時,它的側面積最大?側面積的最大值是多少?
 每個面都是有相同邊數的正多邊形,每個頂點為端點都有相同棱數的凸多面體,叫做正多面體.
每個面都是有相同邊數的正多邊形,每個頂點為端點都有相同棱數的凸多面體,叫做正多面體.
 正多面體有且只有
正多面體有且只有 種.分別是正四面體、正六面體、正八面體、正十二面體、正二十面體.
種.分別是正四面體、正六面體、正八面體、正十二面體、正二十面體.
 簡單多面體:考慮一個多面體,例如正六面體,假定它的面是用橡膠薄膜做成的,如果充以氣體,那么它就會連續(不破裂)變形,最后可變為一個球面.如圖:象這樣,表面經過連續變形可變為球面的多面體,叫做簡單多面體.
簡單多面體:考慮一個多面體,例如正六面體,假定它的面是用橡膠薄膜做成的,如果充以氣體,那么它就會連續(不破裂)變形,最后可變為一個球面.如圖:象這樣,表面經過連續變形可變為球面的多面體,叫做簡單多面體.
說明:棱柱、棱錐、正多面體等一切凸多面體都是簡單多面體
 五種正多面體的頂點數、面數及棱數:
五種正多面體的頂點數、面數及棱數:
|
正多面體 |
頂點數 |
面數 |
棱數 |
|
正四面體 |
 |
 |
 |
|
正六面體 |
 |
 |
 |
|
正八面體 |
 |
 |
 |
|
正十二面體 |
 |
 |
 |
|
正二十面體 |
 |
 |
 |
 歐拉定理(歐拉公式):簡單多面體的頂點數
歐拉定理(歐拉公式):簡單多面體的頂點數 、面數
、面數 及棱數
及棱數 有關系式:
有關系式:
 計算棱數
計算棱數 常見方法:
常見方法:
 ;
;
 各面多邊形邊數和的一半;
各面多邊形邊數和的一半;
 頂點數與共頂點棱數積的一半.
頂點數與共頂點棱數積的一半.
 球的概念: 與定點距離等于或小于定長的點的集合,叫做球體,簡稱球
球的概念: 與定點距離等于或小于定長的點的集合,叫做球體,簡稱球 定點叫球心,定長叫球的半徑
定點叫球心,定長叫球的半徑 與定點距離等于定長的點的集合叫做球面.一個球或球面用表示它的球心的字母表示,例如球
與定點距離等于定長的點的集合叫做球面.一個球或球面用表示它的球心的字母表示,例如球
 球的截面:用一平面
球的截面:用一平面 去截一個球
去截一個球 ,設
,設 是平面
是平面 的垂線段,
的垂線段, 為垂足,且
為垂足,且 ,所得的截面是以球心在截面內的射影為圓心,以
,所得的截面是以球心在截面內的射影為圓心,以 為半徑的一個圓,截面是一個圓面.
為半徑的一個圓,截面是一個圓面.
球面被經過球心的平面截得的圓叫做大圓,被不經過球心的平面截得的圓叫做小圓
 兩點的球面距離:球面上兩點之間的最短距離,就是經過兩點的大圓在這兩點間的一段劣弧的長度,我們把這個弧長叫做兩點的球面距離.
兩點的球面距離:球面上兩點之間的最短距離,就是經過兩點的大圓在這兩點間的一段劣弧的長度,我們把這個弧長叫做兩點的球面距離. (
( 為球心角的弧度數).
為球心角的弧度數).
 球的表面積和體積公式:
球的表面積和體積公式: ,
, .
.
 (
( 安徽)在正方體上任意選擇
安徽)在正方體上任意選擇 個頂點,它們可能是如下各種幾何形體的
個頂點,它們可能是如下各種幾何形體的 個頂點,這些幾何形體是 (寫出所有正確結論的編號).
個頂點,這些幾何形體是 (寫出所有正確結論的編號).
①矩形;②不是矩形的平行四邊形;③有三個面為等腰直角三角形,有一個面為等邊三角形的四面體;④每個面都是等邊三角形的四面體;⑤每個面都是直角三角形的四面體.  (
( 北京春) 兩個完全相同的長方體的長、寬、高分別為
北京春) 兩個完全相同的長方體的長、寬、高分別為 ,
, ,
, ,
,
把它們重疊在一起組成一個新長方體,在這些新長方體中,最長的對角線的長度是




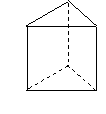
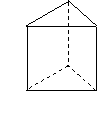
 (
( 上海)有兩個相同的直三棱柱,高為
上海)有兩個相同的直三棱柱,高為 ,底面
,底面
三角形的三邊長分別為 、
、 、
、 (
( ).用它們
).用它們
拼成一個三棱柱或四棱柱,在所有可能的情況中,全面積
最小的是一個四棱柱,則 的取值范圍是
的取值范圍是
 (
( 上海春)正四棱錐底面邊長為
上海春)正四棱錐底面邊長為 ,側棱長為
,側棱長為 ,則其體積為
,則其體積為
 (
( 全國Ⅰ)一個等腰直角三角形的三個頂點分別在正三棱柱的三條側棱上.已知正三棱柱的底面邊長為
全國Ⅰ)一個等腰直角三角形的三個頂點分別在正三棱柱的三條側棱上.已知正三棱柱的底面邊長為 ,則該三角形的斜邊長為
,則該三角形的斜邊長為
 (
( 江蘇)正三棱錐
江蘇)正三棱錐 高為
高為 ,側棱與底面所成角為
,側棱與底面所成角為 ,則點
,則點 到側面
到側面 的距離是
的距離是
 一個正三棱錐與一個正四棱錐,它們的棱長都相等,把這個正三棱錐的一個側面重合在正四棱錐的一個側面上,這個組合體可能是
一個正三棱錐與一個正四棱錐,它們的棱長都相等,把這個正三棱錐的一個側面重合在正四棱錐的一個側面上,這個組合體可能是
 正四棱錐
正四棱錐
 正五棱錐
正五棱錐
 斜三棱柱
斜三棱柱  正三棱柱
正三棱柱
 如果三棱錐
如果三棱錐 的底面是不等邊三角形,側面與底面所成的二面角相等,且
的底面是不等邊三角形,側面與底面所成的二面角相等,且
頂點 在底面的射影為
在底面的射影為 ,
, 在
在 內,那么
內,那么 是
是 的
的
 垂心
垂心  重心
重心  外心
外心  內心
內心
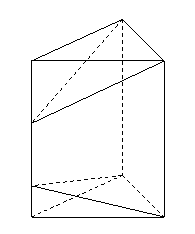
 如圖,在直三棱柱
如圖,在直三棱柱 中,
中, ,
,
 ,
, 、
、 為側棱
為側棱 上的兩點,且
上的兩點,且 ,
,
則多面體 的體積等于
的體積等于
 過棱錐高的三等分點作兩個平行于底面的截面,它們將棱錐的側面分成三部分的面積的比(自上而下)為
過棱錐高的三等分點作兩個平行于底面的截面,它們將棱錐的側面分成三部分的面積的比(自上而下)為
 在三棱錐
在三棱錐 中,
中, ,則側棱
,則側棱 與側面
與側面 所成的角的大小是
所成的角的大小是
 三棱錐一條側棱長是
三棱錐一條側棱長是 ,和這條棱相對的棱長是
,和這條棱相對的棱長是 ,其余四條棱長都是
,其余四條棱長都是 ,求棱錐的體積.
,求棱錐的體積.
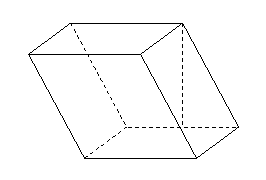
 平行六面體
平行六面體 的底面是矩形,
的底面是矩形,
側棱長為 ,點
,點 在底面
在底面 上的射影
上的射影
 是
是 的中點,
的中點, 與底面
與底面 成
成 角,
角,
二面角 為
為 ,求該平行六面體
,求該平行六面體
的表面積和體積.
 (
( 屆高三合肥市三檢)正三棱柱
屆高三合肥市三檢)正三棱柱 的底面邊長為
的底面邊長為 ,側棱長為
,側棱長為 ,過正三棱柱
,過正三棱柱 底面上的一條棱
底面上的一條棱 作一平面與底面成
作一平面與底面成 的平面角,則該平面與平面
的平面角,則該平面與平面 所截得的線段長等于
所截得的線段長等于
 (
( 屆高三寶雞中學第四次月考)在直四棱柱
屆高三寶雞中學第四次月考)在直四棱柱 中,
中, ,
,  ,
, ,
, ,
, 垂足為
垂足為 .
.
 求證:
求證: ;
; 求異面直線
求異面直線 與
與 所成的角.
所成的角.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com