
 周期函數的定義:對于
周期函數的定義:對于 定義域內的每一個
定義域內的每一個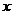 ,都存在非零常數
,都存在非零常數 ,使得
,使得
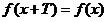 恒成立,則稱函數
恒成立,則稱函數 具有周期性,
具有周期性, 叫做
叫做 的一個周期,
的一個周期,
則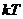 (
(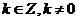 )也是
)也是 的周期,所有周期中的最小正數叫
的周期,所有周期中的最小正數叫 的最小正周期.
的最小正周期.
 幾種特殊的抽象函數:具有周期性的抽象函數:
幾種特殊的抽象函數:具有周期性的抽象函數:
函數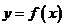 滿足對定義域內任一實數
滿足對定義域內任一實數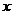 (其中
(其中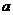 為常數),
為常數),
①
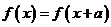 ,則
,則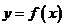 是以
是以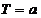 為周期的周期函數;
為周期的周期函數;
②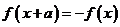 ,則
,則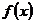 是以
是以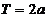 為周期的周期函數;
為周期的周期函數;
③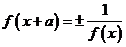 ,則
,則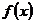 是以
是以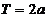 為周期的周期函數;
為周期的周期函數;
④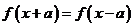 ,則
,則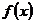 是以
是以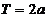 為周期的周期函數;
為周期的周期函數;
⑤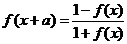 ,則
,則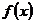 是以
是以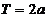 為周期的周期函數.
為周期的周期函數.
⑥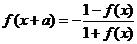 ,則
,則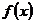 是以
是以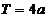 為周期的周期函數.
為周期的周期函數.
⑦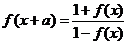 ,則
,則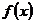 是以
是以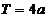 為周期的周期函數.
為周期的周期函數.
⑧函數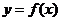 滿足
滿足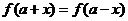 (
( ),若
),若 為奇函數,則其周期為
為奇函數,則其周期為 ,
,
若 為偶函數,則其周期為
為偶函數,則其周期為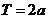 .
.
⑨函數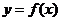
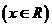 的圖象關于直線
的圖象關于直線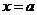 和
和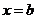
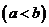 都對稱,則函數
都對稱,則函數 是以
是以
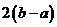 為周期的周期函數;
為周期的周期函數;
⑩函數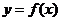
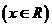 的圖象關于兩點
的圖象關于兩點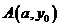 、
、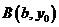
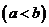 都對稱,則函數
都對稱,則函數 是以
是以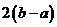 為周期的周期函數;
為周期的周期函數;
⑾函數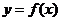
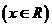 的圖象關于
的圖象關于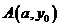 和直線
和直線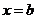
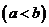 都對稱,則函數
都對稱,則函數 是以
是以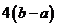 為周期的周期函數;
為周期的周期函數;
 (
(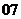 天津)在
天津)在 上定義的函數
上定義的函數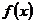 是偶函數,且
是偶函數,且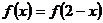 ,若
,若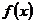 在區間
在區間
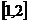 是減函數,則函數
是減函數,則函數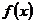
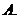 在區間
在區間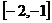 上是增函數,區間
上是增函數,區間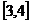 上是增函數
上是增函數
 在區間
在區間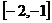 上是增函數,區間
上是增函數,區間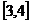 上是減函數
上是減函數
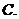 在區間
在區間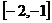 上是減函數,區間
上是減函數,區間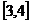 上是增函數
上是增函數
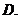 在區間
在區間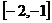 上是減函數,區間
上是減函數,區間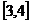 上是減函數
上是減函數
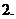 (
(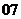 遼寧文)函數
遼寧文)函數 的單調增區間為( )
的單調增區間為( )
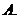
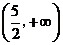


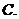
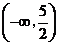
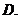
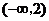
 (
( 福建)已知函數
福建)已知函數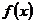 為
為 上的減函數,則滿足
上的減函數,則滿足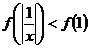 的實數
的實數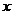 的范圍是
的范圍是 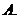


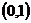
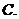
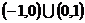
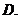
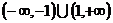
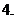 (
( 天津)在
天津)在 上定義的函數
上定義的函數 是偶函數,且
是偶函數,且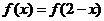 ,若
,若 在區間
在區間
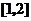 上是減函數,則
上是減函數,則
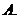 在區間
在區間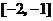 上是增函數,在區間
上是增函數,在區間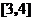 上是增函數
上是增函數
 在區間
在區間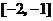 上是增函數,在區間
上是增函數,在區間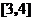 上是減函數
上是減函數
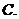 在區間
在區間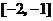 上是減函數,在區間
上是減函數,在區間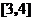 上是增函數
上是增函數
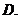 在區間
在區間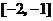 上是減函數,在區間
上是減函數,在區間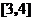 上是減函數
上是減函數
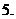 (
(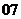 重慶)已知定義域為
重慶)已知定義域為 的函數
的函數 在
在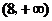 上為減函數,且函數
上為減函數,且函數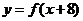
為偶函數,則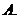


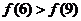
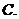
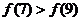
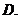
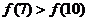
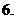 (
( 山東)下列函數既是奇函數,又在區間
山東)下列函數既是奇函數,又在區間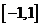 上單調遞減的是
上單調遞減的是
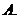
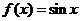

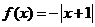
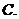
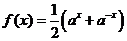
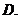
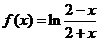
 (
( 天津)若函數
天津)若函數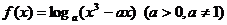 在區間
在區間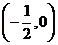 內單調遞增,
內單調遞增,
則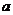 的取值范圍是
的取值范圍是 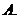
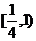

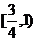
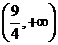
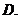
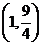
 (
( 重慶)若函數
重慶)若函數 是定義在
是定義在 上的偶函數,在
上的偶函數,在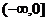 上是減函數,且
上是減函數,且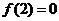 ,
,
則使得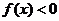 的
的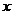 的取值范圍是
的取值范圍是
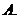
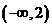 ;
; 
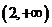 ;
;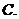
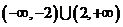 ;
; 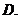
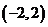
 (
(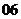 北京文)已知
北京文)已知 是
是 上的增函數,那么
上的增函數,那么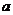 的取值范圍是
的取值范圍是
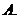
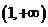

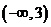
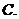
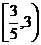
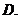
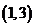
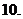 (
( 以前)已知
以前)已知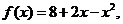 若
若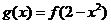 試確定
試確定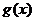 的單調區間和單調性.
的單調區間和單調性.
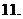 (
( 全國Ⅰ文)設
全國Ⅰ文)設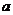 為實數,函數
為實數,函數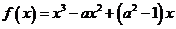 在
在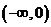 和
和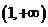 都是增函數,求
都是增函數,求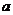 的取值范圍。
的取值范圍。
 (
(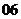 安徽文)設函數
安徽文)設函數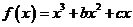
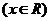 ,已知
,已知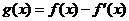 是奇函數。(Ⅰ)求
是奇函數。(Ⅰ)求 、
、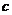 的值。(Ⅱ)求
的值。(Ⅱ)求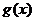 的單調區間與極值。
的單調區間與極值。
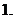 利用函數單調性定義證明:
利用函數單調性定義證明: =
=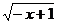 在
在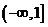 上是減函數
上是減函數
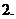 函數
函數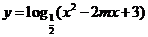 在
在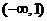 上為增函數,則實數
上為增函數,則實數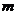 的取值范圍
的取值范圍
 下列函數中,在區間
下列函數中,在區間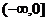 上是增函數的是
上是增函數的是
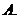
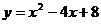

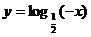
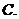
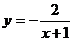
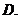

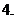 已知
已知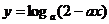 在
在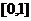 上是
上是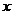 的減函數,則
的減函數,則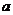 的取值范圍是
的取值范圍是
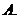
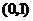

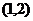
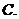

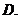
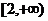
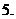
 為
為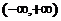 上的減函數,
上的減函數,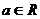 ,則
,則
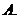
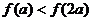

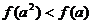
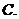
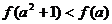
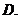
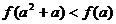
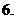 如果奇函數
如果奇函數 在區間
在區間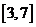 上是增函數,且最小值為
上是增函數,且最小值為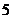 ,那么在區間
,那么在區間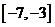 上是
上是
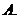 增函數且最小值為
增函數且最小值為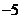
 增函數且最大值為
增函數且最大值為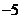
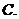 減函數且最小值為
減函數且最小值為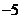
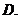 減函數且最大值為
減函數且最大值為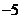
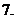 已知
已知 是定義在
是定義在 上的偶函數,它在
上的偶函數,它在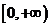 上遞減,那么一定有
上遞減,那么一定有
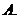
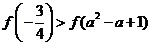

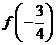 ≥
≥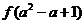
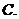
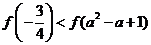
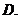
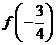 ≤
≤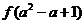
 已知
已知 是偶函數,且在
是偶函數,且在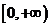 上是減函數,則
上是減函數,則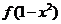 是增函數的區間是
是增函數的區間是
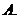
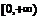

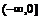
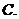
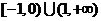
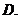

 (
( 湖南文)若
湖南文)若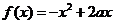 與
與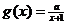 在區間
在區間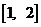 上都是減函數,則
上都是減函數,則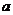
的取值范圍是( )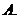
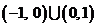

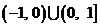
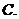
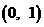
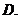

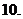 (
(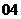 上海)若函數
上海)若函數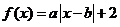 在
在 上為增函數,則實數
上為增函數,則實數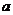 、
、 的范圍是
的范圍是
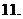 已知偶函數
已知偶函數 在
在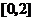 內單調遞減,若
內單調遞減,若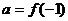 ,
,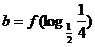 ,
,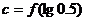 ,則
,則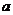 、
、 、
、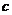 之間的大小關系是_____________
之間的大小關系是_____________
 已知奇函數
已知奇函數 是定義在
是定義在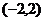 上的減函數,若
上的減函數,若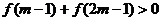 ,求實數
,求實數
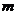 的取值范圍.
的取值范圍.
 已知函數
已知函數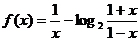 ,求函數
,求函數 的定義域,并討論它的奇偶性和單調性.
的定義域,并討論它的奇偶性和單調性.
 設
設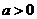 ,
,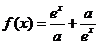 是
是 上的偶函數.
上的偶函數.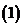 求
求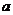 的值;
的值;
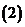 證明
證明 在
在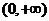 上為增函數.
上為增函數.

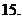 (
( 北京東城模擬)函數
北京東城模擬)函數 對任意的
對任意的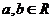 ,都有
,都有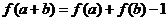 ,
,
并且當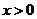 時
時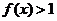 .
.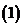 求證:
求證: 是
是 上的增函數;
上的增函數;
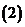 若
若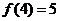 ,解不等式
,解不等式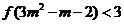

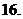 已知函數
已知函數 的定義域是
的定義域是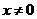 的一切實數,對定義域內的任意
的一切實數,對定義域內的任意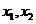 都有
都有
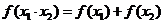 ,且當
,且當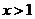 時
時 ,
,
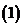 求證:
求證: 是偶函數;
是偶函數;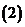
 在
在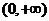 上是增函數;
上是增函數;
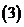 解不等式
解不等式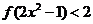 .
.
 函數
函數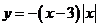 的遞增區間是
的遞增區間是
 已知
已知 是
是 上的奇函數,且在
上的奇函數,且在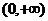 上是增函數,則
上是增函數,則 在
在 上的單調性為
上的單調性為
 已知奇函數
已知奇函數 在
在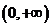 單調遞增,且
單調遞增,且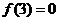 ,則不等式
,則不等式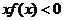 的解集是
的解集是
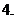 若函數
若函數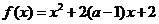 在區間
在區間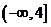 上是減函數,則實數
上是減函數,則實數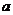 的取值范圍是
的取值范圍是
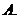


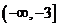
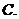
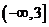
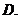
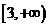
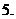 函數
函數 在遞增區間是
在遞增區間是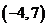 ,則
,則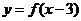 的遞增區間是
的遞增區間是
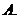
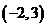

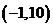
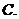
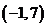
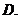
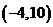
問題1.( 全國,節選
全國,節選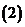 )設函數
)設函數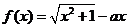 ,其中
,其中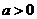 .
.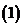 略;
略;
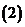 求證:當
求證:當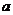 ≥
≥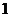 時,函數
時,函數 在區間
在區間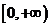 上是單調函數
上是單調函數
問題2.已知函數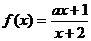 在區間
在區間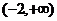 上是增函數,試求
上是增函數,試求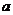 的取值范圍
的取值范圍
問題3.求下列函數的單調區間:
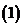
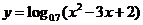
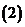
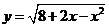
問題4.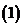 若函數
若函數 在
在 單調遞增,且
單調遞增,且 ,則實數
,則實數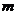 的取值范
的取值范
圍是 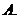
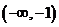

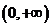
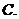
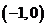
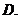
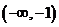
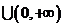
 若
若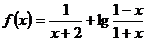 ,則不等式
,則不等式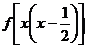 <
<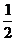 的解集為
的解集為
問題5.( 山東模擬)設
山東模擬)設 是定義在
是定義在 上的函數,且對任意實數
上的函數,且對任意實數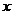 、
、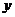 都有
都有
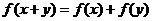 .求證:
.求證: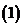
 是奇函數;
是奇函數;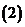 若當
若當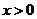 時,有
時,有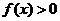 ,
,
則 在
在 上是增函數.
上是增函數.
 討論函數單調性必須在其定義域內進行,因此要研究函數單調性必須先求函數的定義域,函數的單調區間是定義域的子集;
討論函數單調性必須在其定義域內進行,因此要研究函數單調性必須先求函數的定義域,函數的單調區間是定義域的子集;
 判斷函數的單調性的方法有:
判斷函數的單調性的方法有: 用定義;
用定義; 用已知函數的單調性;
用已知函數的單調性; 利用函數的導數;
利用函數的導數;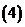 如果
如果 在區間
在區間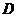 上是增(減)函數,那么
上是增(減)函數,那么 在
在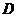 的任一非空子區間上也是增(減)函數
的任一非空子區間上也是增(減)函數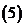 圖象法;
圖象法; 復合函數的單調性結論:“同增異減”
復合函數的單調性結論:“同增異減”  奇函數在對稱的單調區間內有相同的單調性,偶函數在對稱的單調區間內具有相反的單調性.
奇函數在對稱的單調區間內有相同的單調性,偶函數在對稱的單調區間內具有相反的單調性.
 互為反函數的兩個函數具有相同的單調性.
互為反函數的兩個函數具有相同的單調性.
 在公共定義域內,增函數
在公共定義域內,增函數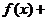 增函數
增函數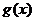 是增函數;減函數
是增函數;減函數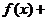 減函數
減函數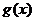 是減函數;增函數
是減函數;增函數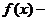 減函數
減函數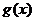 是增函數;減函數
是增函數;減函數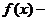 增函數
增函數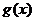 是減函數。
是減函數。
 函數
函數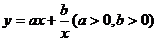 在
在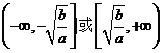 上單調遞增;
上單調遞增;
在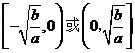 上是單調遞減。
上是單調遞減。
 證明函數單調性的方法:
證明函數單調性的方法: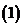 利用單調性定義①;
利用單調性定義①;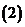 利用單調性定義②
利用單調性定義②
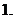 函數單調性的定義:
函數單調性的定義:
①如果函數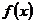 對區間
對區間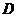 內的任意
內的任意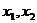 ,當
,當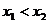 時都有
時都有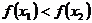 ,則
,則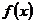 在
在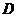 內是增函數;當
內是增函數;當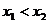 時都有
時都有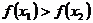 ,則
,則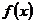 在
在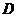 內時減函數。
內時減函數。
②設函數 在某區間
在某區間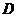 內可導,若
內可導,若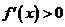 ,則
,則 為
為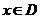 的增函數;若
的增函數;若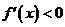 ,則
,則 為
為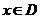 的減函數.
的減函數.
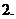 單調性的定義①的等價形式:
單調性的定義①的等價形式:
設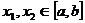 ,那么
,那么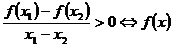 在
在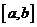 是增函數;
是增函數;
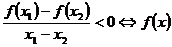 在
在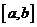 是減函數;
是減函數;
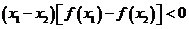
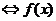 在
在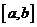 是減函數。
是減函數。
 復合函數單調性的判斷.
復合函數單調性的判斷.
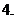 函數單調性的應用.利用定義都是充要性命題.
函數單調性的應用.利用定義都是充要性命題.
即若 在區間
在區間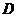 上遞增(遞減)且
上遞增(遞減)且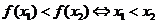 (
(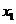
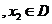 );
);
若 在區間
在區間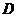 上遞遞減且
上遞遞減且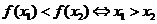 .(
.(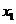
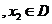 ).
).
①比較函數值的大小②可用來解不等式.③求函數的值域或最值等
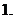 (
(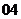 全國)已知函數
全國)已知函數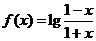 ,若
,若 ,則
,則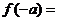
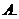

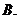
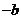
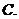
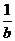
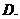
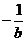
 (
( 全國Ⅰ文)已知函數
全國Ⅰ文)已知函數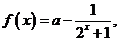 ,若
,若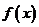 為奇函數,則
為奇函數,則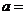
 (
( 江蘇)已知
江蘇)已知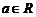 ,函數
,函數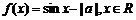 為奇函數,則
為奇函數,則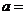
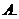

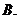

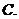
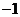
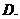
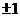
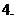 (
(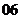 遼寧)設
遼寧)設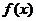 是
是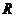 上的任意函數,下列敘述正確的是( )
上的任意函數,下列敘述正確的是( )
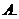
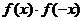 是奇函數
是奇函數 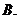
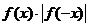 是奇函數
是奇函數
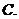
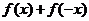 是偶函數
是偶函數 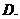
 是偶函數
是偶函數
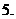 (
( 遼寧文)已知
遼寧文)已知 為奇函數,若
為奇函數,若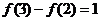 ,則
,則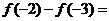
 (
( 廣東)若函數
廣東)若函數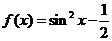
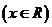 ,則
,則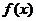 是( )
是( )
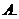 最小正周期為
最小正周期為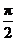 的奇函數
的奇函數 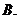 最小正周期為
最小正周期為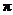 的奇函數
的奇函數
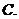 最小正周期為
最小正周期為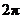 的偶函數
的偶函數 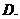 最小正周期為
最小正周期為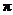 的偶函數
的偶函數
 (
(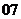 海南)設函數
海南)設函數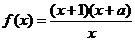 為奇函數,則
為奇函數,則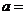
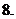 (
(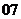 海南文)設函數
海南文)設函數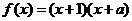 為偶函數,則
為偶函數,則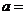
 (
( 江蘇)設
江蘇)設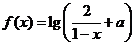 是奇函數,則使
是奇函數,則使 的
的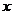 的取值范圍是
的取值范圍是
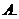
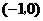
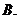
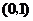
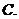
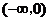
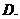
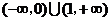
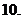 (
(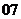 江西)設函數
江西)設函數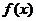 是
是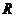 上以
上以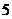 為周期的可導偶函數,則曲線
為周期的可導偶函數,則曲線
在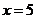 處的切線的斜率為
處的切線的斜率為 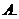
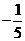
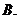

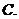
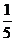
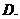
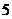
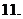 設
設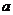 為實數,函數
為實數,函數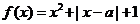 ,
,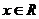 .
.
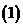 討論
討論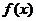 的奇偶性;
的奇偶性;  求
求 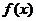 的最小值.
的最小值.
 (
( 上海,本題滿分
上海,本題滿分 分)已知函數
分)已知函數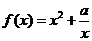
 ,常數
,常數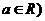 .
.
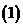 討論函數
討論函數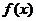 的奇偶性,并說明理由
的奇偶性,并說明理由
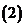 若
若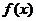 在
在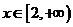 上是增函數,求
上是增函數,求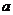 的取值范圍.
的取值范圍.
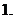 判斷下列函數的奇偶性:
判斷下列函數的奇偶性:
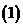
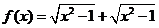 ;
;
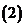
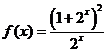 ;
;

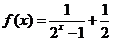 ;
; 
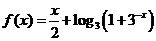 ;
;
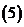
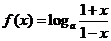 (其中
(其中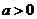 ,
,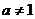 )
)
 (
(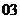 南昌模擬)給出下列函數①
南昌模擬)給出下列函數①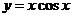 ②
②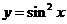 ③
③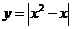 ④
④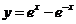 ,
,
其中是奇函數的是( ) 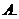 ①②
①② 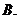 ①④
①④ 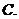 ②④
②④ 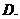 ③④
③④
 已知函數
已知函數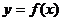 在
在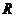 是奇函數,且當
是奇函數,且當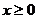 時,
時,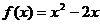 ,則
,則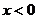 時,
時,
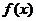 的解析式為_______________
的解析式為_______________
 (
( 上海春)已知函數
上海春)已知函數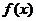 是定義在
是定義在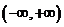 上的偶函數.當
上的偶函數.當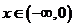 時,
時,
 ,則當
,則當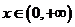 時,
時,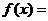
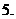 已知
已知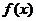 為
為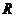 上的奇函數,當
上的奇函數,當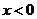 時,
時,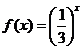 ,那么
,那么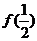 的值為
的值為
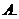
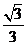
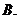
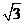
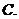
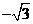
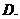
 若
若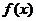 為偶函數,
為偶函數,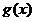 為奇函數,且
為奇函數,且 ,則
,則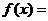 ,
,
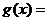
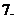 定義在
定義在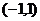 上的函數
上的函數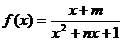 是奇函數,則常數
是奇函數,則常數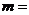 ____,
____,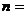 _____
_____
 (
( 北京西城模擬)已知函數
北京西城模擬)已知函數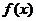 對一切
對一切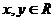 ,都有
,都有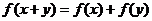 ,
,
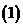 求證:
求證: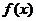 為奇函數;
為奇函數;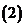 若
若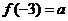 ,用
,用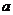 表示
表示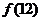 .
.
 (
(  重慶文)已知定義域為
重慶文)已知定義域為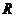 的函數
的函數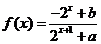 是奇函數。
是奇函數。
(Ⅰ)求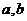 的值;
的值;
(Ⅱ)若對任意的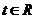 ,不等式
,不等式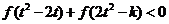 恒成立,求
恒成立,求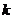 的取值范圍;
的取值范圍;
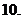 設
設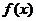 是定義在
是定義在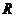 上的奇函數,且
上的奇函數,且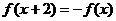 ,又當
,又當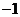 ≤
≤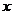 ≤
≤ 時,
時,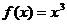 ,
,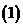 證明:直線
證明:直線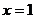 是函數
是函數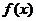 圖象的一條對稱軸;
圖象的一條對稱軸;
 當
當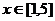 時,求
時,求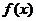 的解析式
的解析式
 已知函數
已知函數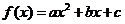 ,
,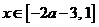 是偶函數,則
是偶函數,則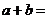
 已知
已知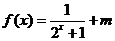 為奇函數,則
為奇函數,則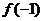 的值為
的值為
 已知
已知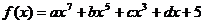 ,其中
,其中 為常數,若
為常數,若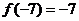 ,
,
則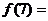 _______
_______
 若函數
若函數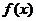 是定義在
是定義在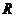 上的奇函數,則函數
上的奇函數,則函數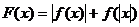 的圖象關于
的圖象關于
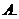
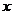 軸對稱
軸對稱 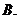
 軸對稱
軸對稱 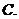 原點對稱
原點對稱  以上均不對
以上均不對
 函數
函數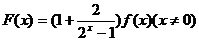 是偶函數,且
是偶函數,且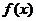 不恒等于零,則
不恒等于零,則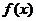
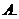 是奇函數
是奇函數
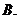 是偶函數
是偶函數
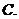 可能是奇函數也可能是偶函數
可能是奇函數也可能是偶函數  不是奇函數也不是偶函數
不是奇函數也不是偶函數
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com