
題目列表(包括答案和解析)
| a |
| x |
| a |
| a |
| b2 |
| x |
| c |
| x2 |
| a |
| x |
| a |
| x2 |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| 2 |
已知函數![]() 有如下性質:如果常數
有如下性質:如果常數![]() ,那么該函數在(0,
,那么該函數在(0,![]() )上減函數,在
)上減函數,在![]() 是增函數。
是增函數。
(1)如果函數![]() 的值域為
的值域為![]() ,求
,求![]() 的值;
的值;
(2)研究函數![]() (常數
(常數![]() )在定義域的單調性,并說明理由;
)在定義域的單調性,并說明理由;
(3)對函數![]() 和
和![]() (常數
(常數![]() )作出推廣,使它們都是你所推廣的函數的特例。研究推廣后的函數的單調性(只須寫出結論,不必證明),并求函數
)作出推廣,使它們都是你所推廣的函數的特例。研究推廣后的函數的單調性(只須寫出結論,不必證明),并求函數
![]() (n是正整數)在區間[
(n是正整數)在區間[![]() ,2]上的最大值和最小值(可利用你的研究結論)。
,2]上的最大值和最小值(可利用你的研究結論)。
已知函數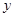 =
=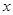 +
+ 有如下性質:如果常數
有如下性質:如果常數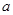 >0,那么該函數在
>0,那么該函數在 0,
0,
 上是減函數,在
上是減函數,在
 ,+∞
,+∞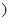 上是增函數.
上是增函數.
(Ⅰ)如果函數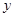 =
=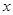 +
+ (
(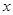 >0)的值域為
>0)的值域為 6,+∞
6,+∞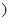 ,求
,求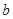 的值;
的值;
(Ⅱ)研究函數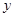 =
=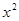 +
+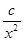 (常數
(常數 >0)在定義域內的單調性,并說明理由;
>0)在定義域內的單調性,并說明理由;
(Ⅲ)對函數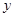 =
=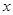 +
+ 和
和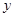 =
=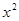 +
+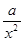 (常數
(常數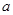 >0)作出推廣,使它們都是你所推廣的函數的特例.研究推廣后的函數的單調性(只須寫出結論,不必證明),并求函數
>0)作出推廣,使它們都是你所推廣的函數的特例.研究推廣后的函數的單調性(只須寫出結論,不必證明),并求函數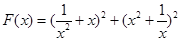 (
(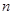 是正整數)在區間[
是正整數)在區間[ ,2]上的最大值和最小值(可利用你的研究結論).
,2]上的最大值和最小值(可利用你的研究結論).
(16分)設 使定義在區間
使定義在區間 上的函數,其導函數為
上的函數,其導函數為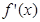 .如果存在實數
.如果存在實數 和函數
和函數 ,其中
,其中 對任意的
對任意的 都有
都有 >0,使得
>0,使得 ,則稱函數
,則稱函數 具有性質
具有性質 .
.
(1)設函數
 ,其中
,其中 為實數
為實數
①求證:函數 具有性質
具有性質
②求函數 的單調區間
的單調區間
(2)已知函數 具有性質
具有性質 ,給定
,給定
 ,
, ,且
,且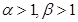 ,若|
,若| |<|
|<| |,求
|,求 的取值范圍
的取值范圍
(16分)設 使定義在區間
使定義在區間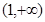 上的函數,其導函數為
上的函數,其導函數為 .如果存在實數
.如果存在實數 和函數
和函數 ,其中
,其中 對任意的
對任意的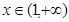 都有
都有 >0,使得
>0,使得 ,則稱函數
,則稱函數 具有性質
具有性質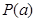 .
.
(1)設函數
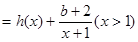 ,其中
,其中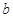 為實數
為實數
①求證:函數 具有性質
具有性質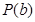
②求函數 的單調區間
的單調區間
(2)已知函數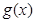 具有性質
具有性質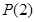 ,給定
,給定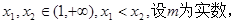
 ,
, ,且
,且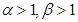 ,若|
,若| |<|
|<| |,求
|,求 的取值范圍
的取值范圍
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com