問題1．
(
湖北)若互不相等的實數
、
、
成等差數列，、、成等比數列，且
，則
(天津)設等差數列
的公差
不為，
．若
是
與
的等比中項，則
(海南)已知
，
，
成等差數列，成等比數列，則
的最小值是 
已知等差數列
的公差
，且
成等比數列，則
(全國Ⅰ)等比數列的前
項和為，已知
，
，
成等差數列，
則的公比為
問題2．(全國Ⅰ文)設是等差數列，
是各項都為正數的等比數列，且
，
，
求，的通項公式；求數列
的前項和．
問題3．(全國Ⅲ)在等差數列中，公差，是與的等比中項，已知數列
成等比數列，求數列的通項
問題4．(屆東北師大附中高三月考)數列
的前項和記作
，滿足
，
．
證明數列
為等比數列；并求出數列的通項公式．
記
，數列的前項和為，求．
問題5.(上海) 已知數列(為正整數)是首項是，公比為的等比數列.
求和：
由的結果歸納概括出關于正整數的一個結論，并加以證明.
解決等差數列和等比數列的問題時，通常考慮兩類方法：①基本量法：即運用條件轉化為關于和
的方程；②巧妙運用等差數列和等比數列的性質，一般地運用性質可以化繁為簡，減少運算量．
深刻領會兩類數列的性質，弄清通項和前項和公式的內在聯系是解題的關鍵．
解題時，還要注重數學思想方法的應用，如“函數與方程”、“數形結合”、“分類討論”、
“化歸轉化”.
等差數列的概念、性質及基本公式。等比數列的概念、性質及基本公式。
(
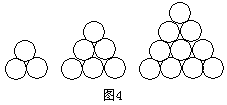
廣東)在德國不萊梅舉行的第屆世乒賽期 間，某商場櫥窗里用同樣的乒乓球堆成若干準“正三棱錐”形的展品，其中第
堆只有一層，就一個乒乓球；第
、
、、…堆最底層(第一層)分別按圖所示方式固定擺放.從第一層開始，每層的小球自然壘放在下一層之上，第
堆第層就放一個乒乓球，以
表示第堆的乒乓球總數，則
；
(答案用表示).
(福建)數列
的前項和為
，若
，則等于
(全國Ⅱ)已知數列的通項
，其前項和為，則
(福建文)“數列
的前項和為，
，
．
(Ⅰ)求數列的通項；
(Ⅱ)求數列
的前項和
．
(荊州統測)數列滿足遞推關系：，且，
.
求、；
求；
求數列的前項和.
(北京)設
，則等于
明朝程大拉作數學詩：“遠望巍巍塔七層，紅光點點加倍增，共燈三百八十一，請問尖頭 盞燈”.
求數列，
，
，
，…的前項和.
…
在數列中，
…
，又
，則數列
的前 項和為
求數列
，
，
，，…的前項和.
問題1．求下列數列前項和： 
，
，
，…，
；
，
，
，…，
；，
，
，…，
；
，
，
，…，
， 
；
…
； ，
，
，…，；
問題2．求和
；
； 
問題3．已知數列的通項
，求其前項和
問題4．(全國Ⅰ文)設正項等比數列的首項
，前項和為
，且
.(Ⅰ)求的通項；(Ⅱ)求的前項和.
問題5．(湖北)已知二次函數
的圖像經過坐標原點，其導函數為
，數列的前項和為，點
均在函數的圖像上.(Ⅰ)求數列的通項公式；(Ⅱ)設
，是數列
的前項和，求使得
對所有
都成立的最小正整數
；
基本公式法：等差數列求和公式：
等比數列求和公式：
；
； 
.
錯位相消法：給
各邊同乘以一個適當的數或式，然后把所得的等式和原等式相減，對應項相互抵消，最后得出前項和.
一般適應于數列
的前向求和，其中成等差數列，成等比數列。
分組求和：把一個數列分成幾個可以直接求和的數列，然后利用公式法求和。
拆項(裂項)求和：把一個數列的通項公式分成兩項差的形式，相加過程中消去中間項，只剩下有限項再求和.
常見的拆項公式有：
若是公差為的等差數列，則
；
；
；
；
；
；
；
倒序相加法：根據有些數列的特點，將其倒寫后與原數列相加，以達到求和的目的。
導數法：靈活利用求導法則有時也可以完成數列求和問題的解答.
遞推法.奇偶分析法.
等差數列與等比數列的求和公式的應用；
倒序相加、錯位相減，分組求和、拆項求和等求和方法；
(
陜西)各項均為正數的等比數列
的前
項和為
為，若
，
，
則
等于 
(遼寧)在等比數列
中,
,前項和為,若數列
也是等比數列,則
等于
(湖北)設等比數列
的公比為
，前項和為，若
，，
成等差數列，則的值為
(全國文Ⅱ)設等比數列的公比
，前項和為．已知
，
求的通項公式．
(北京)數列中，
(
是常數，
)，且
成公比不為
的等比數列．(Ⅰ)求的值；(Ⅱ)求的通項公式．
(山東)設數列滿足
，
．
(Ⅰ)求數列的通項；(Ⅱ)設
，求數列
的前項和．
(福建文)已知數列滿足
(Ⅰ)證明：數列
是等比數列；
(Ⅱ)求數列的通項公式；
(Ⅲ)若數列滿足
證明是等差數列。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com