
 (
( 廣東)已知數列
廣東)已知數列 的前
的前 項和
項和 ,第
,第 項滿足
項滿足 ,則
,則








 (
( 北京文)若數列
北京文)若數列 的前
的前 項和
項和
 ,則此數列的通項公式為
,則此數列的通項公式為
 (
( 江西)已知數列
江西)已知數列 對于任意
對于任意 ,有
,有 ,若
,若 ,則
,則

 (
( 全國)已知數列
全國)已知數列 的前
的前 項和
項和 滿足
滿足
 寫出數列
寫出數列 的前三項
的前三項 ;
;
 求數列
求數列 的通項公式;
的通項公式;
 (
( 全國Ⅰ)已知數列
全國Ⅰ)已知數列 中
中 ,且
,且 ,
,
其中 … (Ⅰ)求
… (Ⅰ)求 ,
, (Ⅱ)求
(Ⅱ)求 的通項公式.
的通項公式.
 (
( 全國)已知數列
全國)已知數列 ,滿足
,滿足 ,
, …
… ,則
,則 的通項
的通項
 (
( 天津)在數列
天津)在數列 中,
中, ,
, ,且
,且 ,
,
則
 已知數列
已知數列 中,
中, ,對所有的
,對所有的 ,都有
,都有 …
… ,則
,則








 數列
數列 中,
中, ,
, (
( ≥
≥ ),則
),則 等于
等于






 不存在
不存在
 數列
數列 中,
中, ,
, (
( ≥
≥ )求其通項公式.
)求其通項公式.
 數列
數列 滿足
滿足
 ,若
,若 ,則
,則 ;
;
 (
( 重慶)在數列
重慶)在數列 中,若
中,若 ,
, (
( ≥
≥ ),則該數列的通項
),則該數列的通項
 已知
已知
 ,則數列
,則數列 的最大項是
的最大項是





 或
或
 不存在
不存在
 (
( 南通市九校聯考)已知數列
南通市九校聯考)已知數列 中,
中,
 ,則在數列
,則在數列 的前
的前 項中最小項和最大項分別是
項中最小項和最大項分別是

 ,
,

 ,
,

 ,
,

 ,
,
 已知函數
已知函數 ,設數列
,設數列 滿足:
滿足: (
( 且
且 ),
), ,
,
 為數列
為數列 的前
的前 項和.
項和. 若
若 ,求
,求 ,
, ,
, ;
; 求證:數列
求證:數列 是周期數列;
是周期數列; 探究:是否存在滿足
探究:是否存在滿足 的
的 ,使
,使 ?
?
 已知
已知 ,則
,則
 在數列
在數列 中,
中, ,且
,且 ,則
,則
 在數列
在數列 中,
中, ,
, ,且
,且 ,則
,則
 (
( 湖南文)已知數列
湖南文)已知數列 滿足
滿足
 ,則
,則








 (
( 屆高三湖南師大附中第二次月考)若數列
屆高三湖南師大附中第二次月考)若數列 滿足
滿足 ,
, ,
,

 ,則
,則 等于
等于 








問題1. 根據下面各數列的前幾項值,寫出數列的一個通項公式:

 ,
, ,
, ,
, ,
, ,…;
,…; 
 ,
, ,
, ,
, ,
, ,…;
,…;

 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,…;
,…;
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,…;
,…;

 ,
, ,
, ,
, ,
, ,
, ,…;
,…; 
 ,
, ,
, ,
, ,
, ,…;
,…;

 ,
, ,
, ,
, ,
, ,…;
,…; 
 ,
, ,
, ,
, ,…;
,…;
問題2.根據下列各個數列 的首項和遞推關系,求其通項公式:
的首項和遞推關系,求其通項公式:

 ,
,
 ;
;
 ,
,
 ;
;

 ,
, ,
, ;
; 
 ,
,

問題3.已知下面各數列 的前
的前 項和
項和 ,求
,求 的通項公式:
的通項公式:

 ;
;


問題4. 求數列
求數列 中的最大項;
中的最大項;
 已知數列
已知數列 的通項公式
的通項公式 ,求
,求 為何值時,
為何值時, 取最大值.
取最大值.
問題5.設
 ,又知數列
,又知數列 的通項
的通項 滿足
滿足
 ,
, 試求數列
試求數列 的通項公式;
的通項公式; 判斷數列
判斷數列 的增減性.
的增減性.
數列通項公式的求法: 觀察分析法;
觀察分析法; 公式法:
公式法:
 轉化成等差、等比數列;
轉化成等差、等比數列; 累加、累乘法 ;
累加、累乘法 ; 遞推法。
遞推法。
 數列的有關概念;
數列的有關概念;
 數列的表示方法:
數列的表示方法: 列舉法;
列舉法; 圖象法;
圖象法; 解析法(通項公式);
解析法(通項公式); 遞推法.
遞推法.

 與
與 的關系:
的關系: .
.
 集合
集合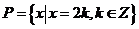 ,
,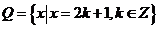 ,
,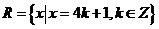 ,
,
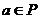 ,
,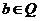 ,設
,設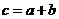 ,則有( )
,則有( )
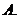
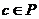
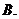
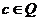
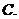
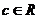
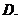 以上都不對
以上都不對
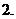 若
若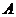 、
、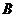 是全集
是全集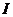 的真子集,則下列四個命題①
的真子集,則下列四個命題①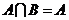 ;②
;②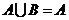 ;
;
③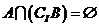 ;④
;④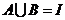 .中與命題
.中與命題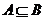 等價的有( )
等價的有( )
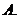
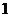 個
個
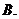
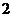 個
個
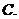
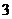 個
個 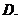
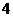 個
個
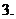 集合
集合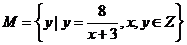 的元素個數是( )
的元素個數是( )
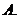
 個
個
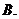
 個
個 
 個
個
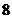 個
個
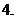 集合
集合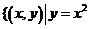 且
且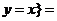

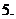 如圖,
如圖,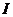 為全集,
為全集,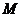 、
、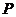 、
、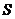 是
是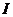 的三個子集,則陰影部分所表示的集合是( )
的三個子集,則陰影部分所表示的集合是( )
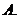
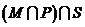
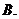
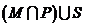
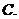
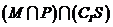
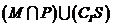
 已知集合
已知集合 ,
,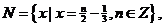
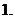 選擇:集合
選擇:集合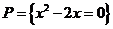 ( )、
( )、 ( )、
( )、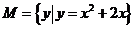 ( )、
( )、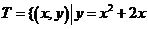 且
且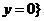 ( ).
( ).
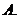
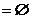
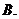
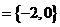
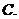
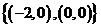
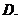 恰有一個元素
恰有一個元素 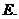
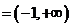
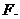

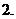 (
( 上海)已知集合
上海)已知集合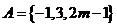 ,集合
,集合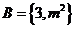 ,若
,若 ,則實數
,則實數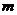 的值為
的值為
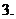 滿足
滿足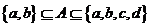 的集合
的集合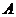 的個數有
個;
的個數有
個;
滿足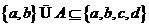 的集合
的集合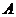 的個數有
個.
的個數有
個.
(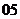 湖北)設
湖北)設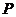 、
、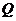 為兩個非空實數集合,定義集合
為兩個非空實數集合,定義集合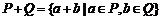 ,
,
若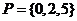 ,
, ,則
,則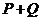 中元素的個數是( )
中元素的個數是( )
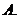
 調查某班
調查某班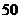 名學生,音樂愛好者
名學生,音樂愛好者 名,體育愛好者
名,體育愛好者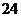 名,則兩方面都愛好的人數最少是
,最多是
名,則兩方面都愛好的人數最少是
,最多是
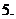
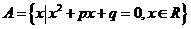
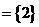 ,則
,則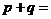
問題1:已知集合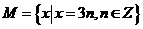 ,
,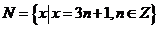 ,
,
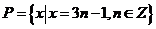 ,且
,且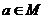 ,
,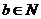 ,
,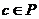 ,設
,設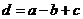 ,則
,則
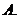
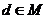
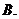
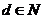
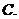
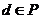
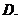
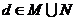
問題2:設集合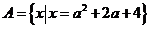 ,
,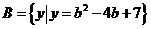 .
.
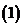 若
若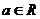 ,
,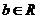 ,試確定集合
,試確定集合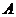 與集合
與集合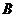 的關系;
的關系;
 若
若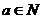 ,
,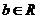 ,試確定集合
,試確定集合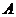 與集合
與集合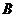 的關系.
的關系.
問題3: 年第
年第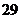 屆奧運會將在北京召開,現有三個實數的集合,既可以表示
屆奧運會將在北京召開,現有三個實數的集合,既可以表示
為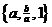 ,也可以表示為
,也可以表示為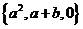 ,則
,則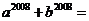
問題4:(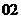 新課程)設
新課程)設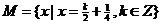 ,
, 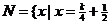 ,
,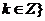
則
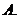

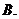

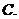
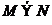
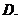
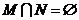
問題5:①若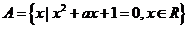 ,
, 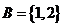 ,且
,且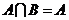 ,求
,求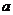 的范圍
的范圍
②設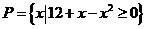 ,
,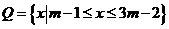 ,若
,若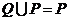 ,求
,求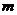 的范圍
的范圍
[機動]設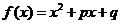 ,
,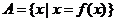 ,
,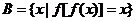 ,
,
(1)求證: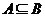 ;
;
(2)如果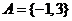 ,求
,求 .
.
 解決集合問題,首先要弄清楚集合中的元素是什么,即元素分析法的掌握.
解決集合問題,首先要弄清楚集合中的元素是什么,即元素分析法的掌握.
 弄清集合中元素的本質屬性,能化簡的要化簡;
弄清集合中元素的本質屬性,能化簡的要化簡;
 抓住集合中元素的
抓住集合中元素的 個性質,對互異性要注意檢驗;
個性質,對互異性要注意檢驗;
 正確進行“集合語言”和普通“數學語言”的相互轉化.
正確進行“集合語言”和普通“數學語言”的相互轉化.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com